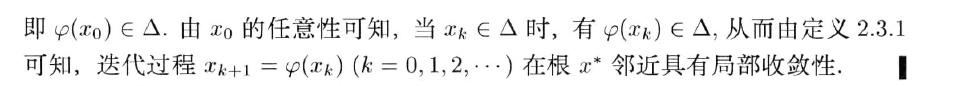数值计算方法与实验
第一章 算法与误差
1.1 算法
1.1.1 计算方法简介
- 计算方法又称数值分析,它是研究用计算机求解各种数学问题的数值解法及其理论并由软件实现的一门学科,计算数学是数学科学的一个分支,计算方法是计算数学的一个主要部分。
- ①实际问题→②建立数学模型→③构造数值计算方法→④程序设计→⑤上机计算求出结果
1.1.2 研究算法的意义
- 科学计算离不开计算机,更离不开算法设计,人类的计算能力是计算机的研制能力与算法的设计能力两者的总和。一位著名学者尖锐指出,如果提供不出高效算法,超级计算机客观上只是一堆“超级废铁”,可见,研究实用的数值方法是很有意义的。
1.2 误差
- 一般来说,数值计算都是近似计算,求得的结果都是有误差的,因此,误差分析和估计是数值计算过程中的重要内容,通过它们可以确切地知道误差的性态和误差的界,近似值与准确值之差,称为误差,按其来源,可分为模型误差、测量误差、截断误差和舍入误差等。
1.2.1 误差与有效数字
1.2.2 数值运算的误差估计
1.2.3 病态问题与条件数
1.2.4 算法设计原则
- 防止大数“吃掉”小数
- 避免两个相近数相减
- 避免大数作乘数和小数作除数
- 渐少运算次数,避免误差积累
1.3 上机实验举例

public class main {
public static void main(String[] args)
{
int i=1;
double y,y0;
y0=Math.log(6.0)-Math.log(5.0);
System.out.print("y["+(i-1)+"]="+y0+" ");
while(i<=20){
y=1.0/i-5*y0;
y0=y;
i++;
System.out.print("y["+(i-1)+"]="+y0+" ");
if(i%3==0){
System.out.println("");
}
}
}
}
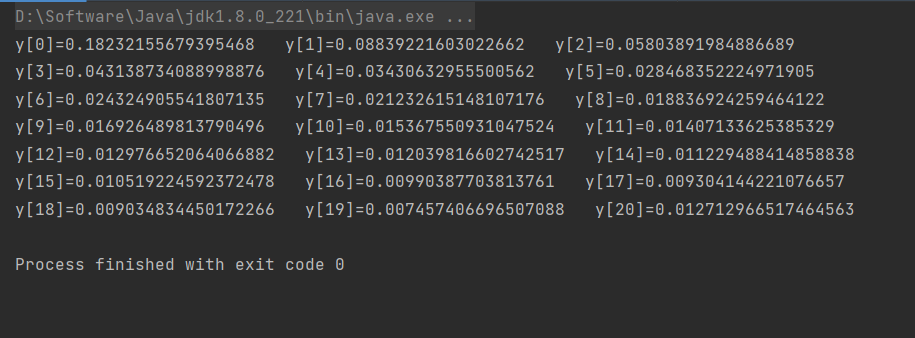

public class main {
public static void main(String[] args)
{
int i=20;
double y,y0;
y0=(1.0/126.0+1.0/105.0)/2.0;
System.out.print("y["+(i)+"]="+y0+" ");
while(i>=1){
y=1.0/(5.0*i)-(1.0/5.0)*y0;
y0=y;
i--;
System.out.print("y["+(i)+"]="+y0+" ");
if(i%3==0){
System.out.println("");
}
}
}
}

1.4 习题


import java.util.Scanner;
public class main {
public static void main(String[] args)
{
int i,j;
double x,y=1,endY;
Scanner reader = new Scanner(System.in);
System.out.print("计算x的256次方,请先输入x的值:");
x=reader.nextFloat();
endY=x;
for(i=1;i<=8;i++){
y=x*y;
x=y;
endY=y*endY;
}
System.out.print("x**256="+endY);
}
}
第二章 非线性方程的数值解法

2.1 根的隔离

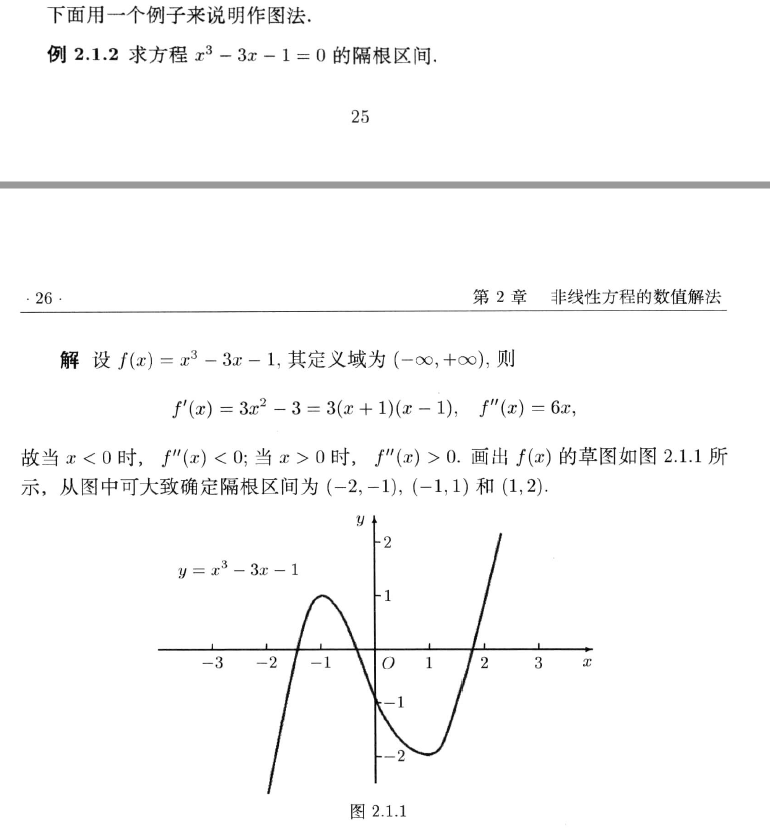
- 二阶导数体现函数的凹凸性,二阶导大于等于0,函数为凹函数,二阶导小于等于0,函数为凸函数。
- 扫描法

2.2 二分法
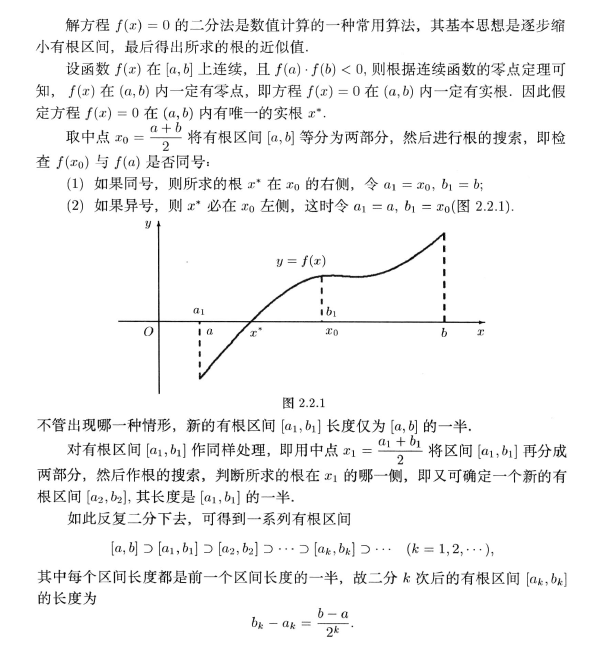

- 二分法的优点是算法简单,且总是收敛的,缺点是收敛太慢,故一般不单独将其用于求根,只用其为根求得一个较好的近似值。
2.3 迭代法及其收敛性
- 迭代法求根过程分两步,第一步先提供根的某个猜测值,即所谓迭代初值,然后再将迭代初值逐步加工成满足精度要求的根。
2.3.1 迭代法的设计思想

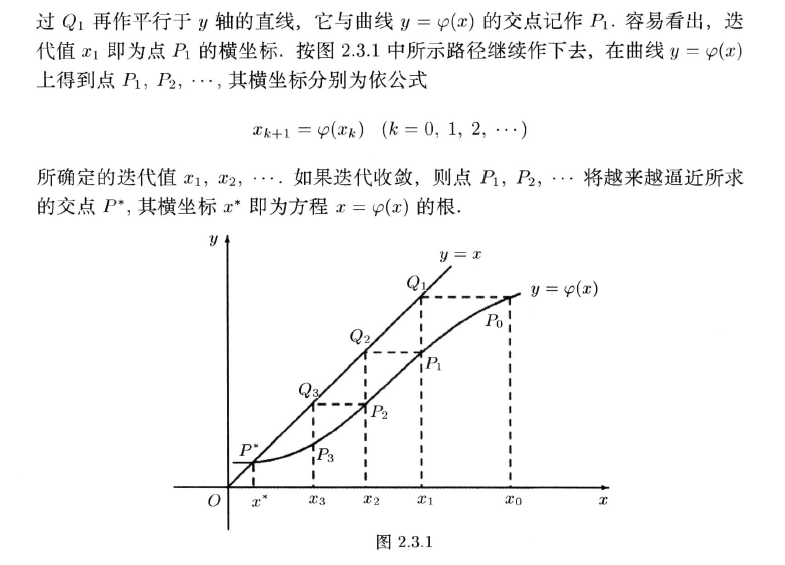
2.3.2 全局收敛性



2.3.3 局部收敛性与收敛阶



2.4 迭代的加速方法
- 对于收敛的迭代过程,只要迭代只够多次,就可以使结果达到任意的精度,但有时迭代过程收敛缓慢,从而使计算量变得很大,因此迭代过程的加速是个重要的课题。
2.4.1 埃特金(Aitken)加速法


2.4.2 斯蒂芬森(Steffensen)迭代法


2.5 牛顿(Newton)法
2.5.1 牛顿公式的导出


2.5.2 牛顿法在单根附近的收敛性

2.5.3 牛顿法的应用

2.5.4 简化牛顿法与牛顿下山法

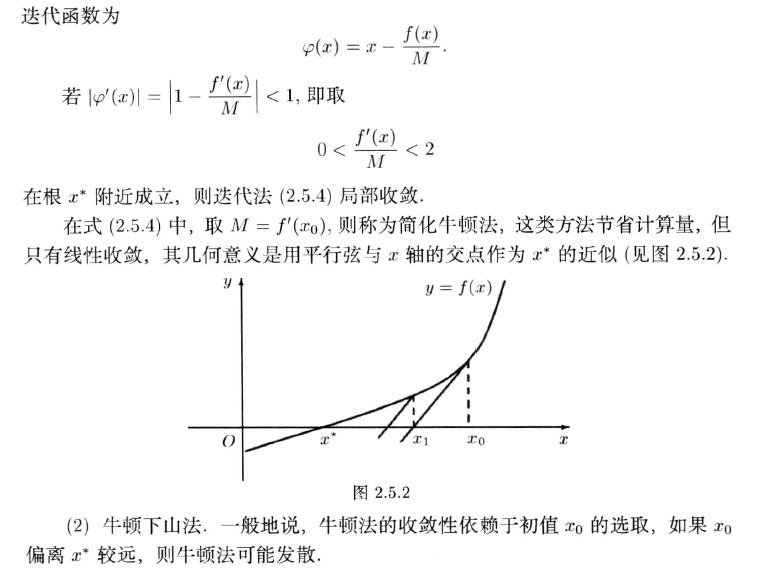
2.5.5 重根情形

2.6 弦截法与抛物线法

2.6.1 弦截法




2.6.2抛物线法

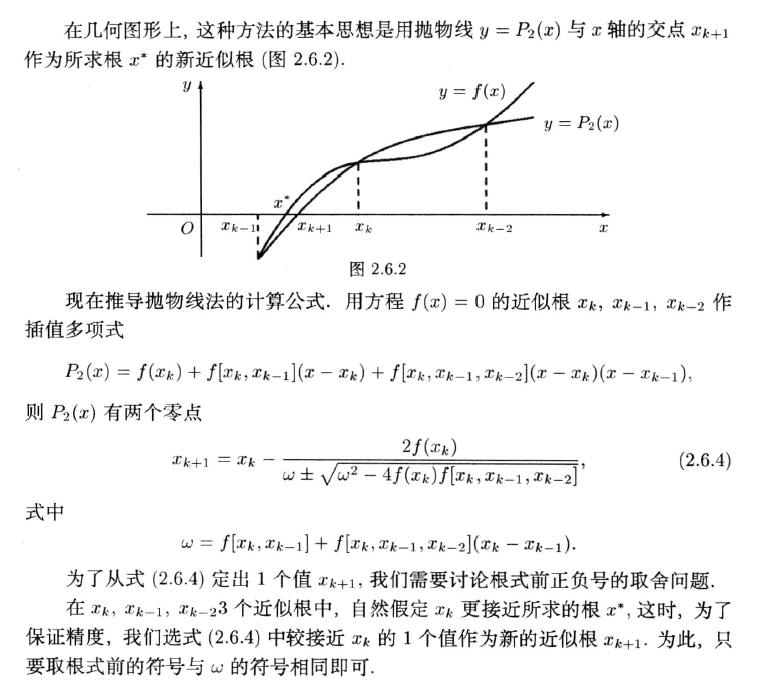
2.7 上机实验举例

习题
第三章 方程组与矩阵特征值、特征向量的求解
3.1 向量和矩阵的范数
3.1.1 向量的范数
3.1.2 矩阵的范数
3.1.3 谱半径
3.1.4 矩阵的条件数
3.2 迭代法
3.2.1 迭代法的一般形式
3.2.2 雅可比(Jacobi)迭代法
3.2.3 高斯-塞德尔(Gauss-Seidel)迭代法
3.2.4 超松弛迭代法
3.2.5 迭代法得收敛性
3.3 解非线性方程组的牛顿迭代法
3.4 消去法
3.4.1 约当消去法
3.4.2 高斯消去法
3.4.3 主元素消去法
3.4.4 矩阵的LU分解
3.5 追赶法
3.6 平方根法
3.7 矩阵分解方法
3.8 矩阵的特征值与特征向量的计算
3.8.1 乘幂法
3.8.2 原点位移法
3.8.3 反幂法
3.9 上机实验举例
第四章 插值与拟合
4.1 泰勒插值
4.2 拉格朗日插值
4.2.1 线性插值
4.2.2 抛物插值
4.2.3 一般情形的拉格朗日插值公式
4.2.4 拉格朗日余项定理
4.3 牛顿插值
4.3.1 差商的定义及其基本性质
4.3.2 差商形式的插值公式
4.4 差分形式的插值
4.4.1 差分的概念
4.4.2 差分形式的插值公式
4.5 埃尔米特插值
4.6 分段插值法
4.6.1 高次插值的龙格(Runge)现象
4.6.2 分段插值的概念
4.6.3 分段线性插值
4.6.4 分段三次插值
4.7 样条插值
4.7.1 样条函数的概念
4.7.2 三次样条插值
4.7.3 样条插值函数的建立
4.7.4 误差界与收敛性
4.8 曲线拟合的最小二乘法
4.8.1 最小二乘法
4.8.2 线性拟合
4.8.3 多项式拟合
4.8.4 指数函数型与幂函数型的拟合
4.9 上机实验举例
第五章 数值积分与数值微分
5.1 数值积分的基本概念
5.1.1 数值求积的基本思想
5.1.2 代数精度的概念
5.1.3 插值型的求积公式
5.1.4 求积公式的收敛性与稳定性
5.2 牛顿-柯特斯(Newton-Cotes)公式
5.2.1 公式的导出
5.2.2 偶阶求积公式的代数精度
5.3 复化求积公式
5.4 龙贝格(Romberg)求积公式
5.4.1 梯形法的递推化
5.4.2 龙贝格公式
5.5 高斯求积公式
5.6 数据的积分
5.7 开放积分公式
5.8 重积分的计算
5.9 数值微分
5.9.1 差商公式的导出
5.9.2 中点方法的加速(理查逊外推加速法)
5.9.3 插值型的求导公式
5.10 上机实验举例
第六章 常微分方程的数值解法
6.1 欧拉方法
6.1.1 欧拉方法及改进的欧拉方法
6.1.2 局部截断误差与精度
6.2 龙格-库塔方法
6.3 亚当姆斯方法
6.4 收敛性与稳定性
6.5 方程组与高阶方程
6.6 边值问题
6.6.1 打靶法
6.6.2 有限差分法
上机实验举例