复杂网络模型
复杂网络的基本概念
现实意义
- 刻画基因、蛋白质和代谢体之间交互关系的网络,把各个部分有机地组织成鲜活地细胞。细胞网络的存在是生命的必要条件。
- 刻画神经元之间连接关系的神经网络,是我们理解大脑运转方法和人类意识的关键。
- 职场关系、朋友关系和家庭关系的总和通常被称为社会网络。社会网络是人类社会的重要组成部分,决定着知识、行为和资源在社会中的传播。
- 描述通信设备之间通过电缆或无线彼此交互的通信网络,是现代通信系统的核心。
- 由发电机和传输线路构成的电网为几乎所有现代技术提供着能源。
- 人们彼此交换物品和服务而形成的贸易网络,是第二次世界大战以来世界物质繁荣的基础。
社会影响


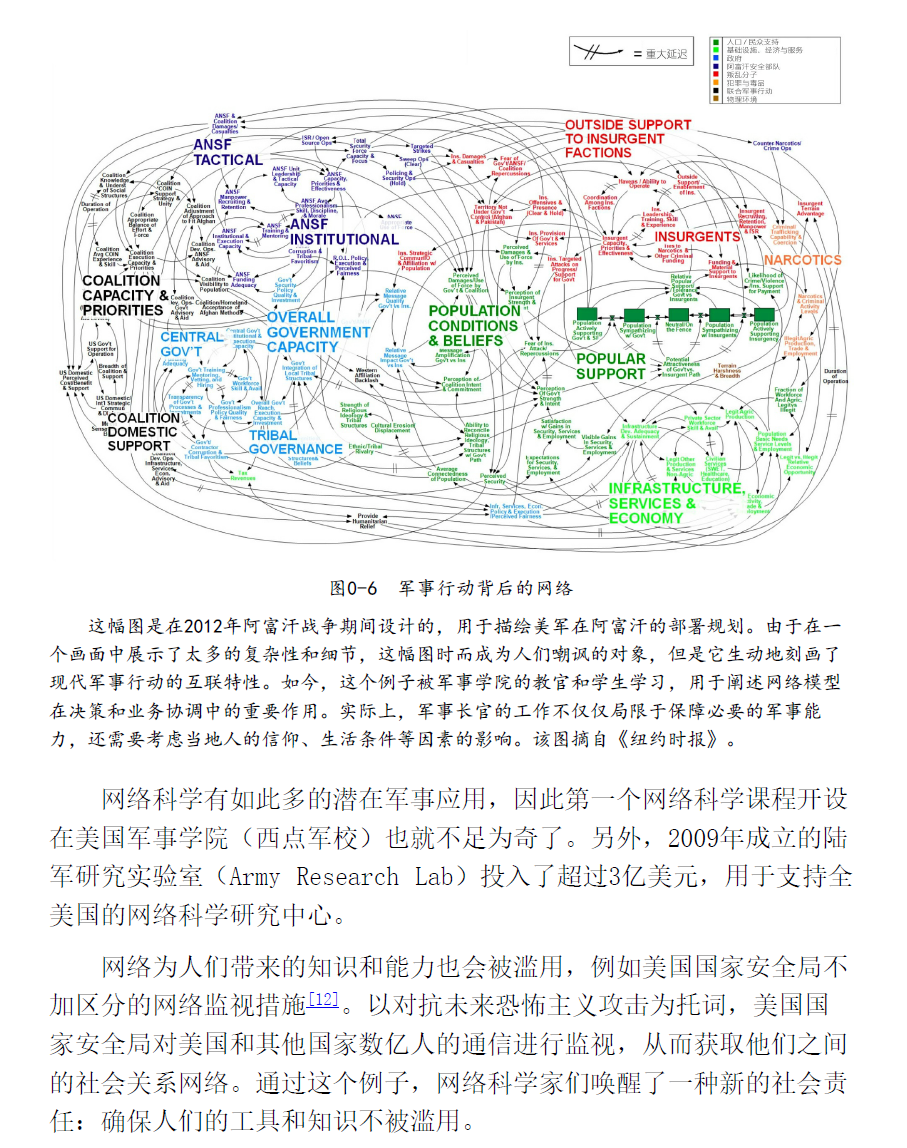



科学影响


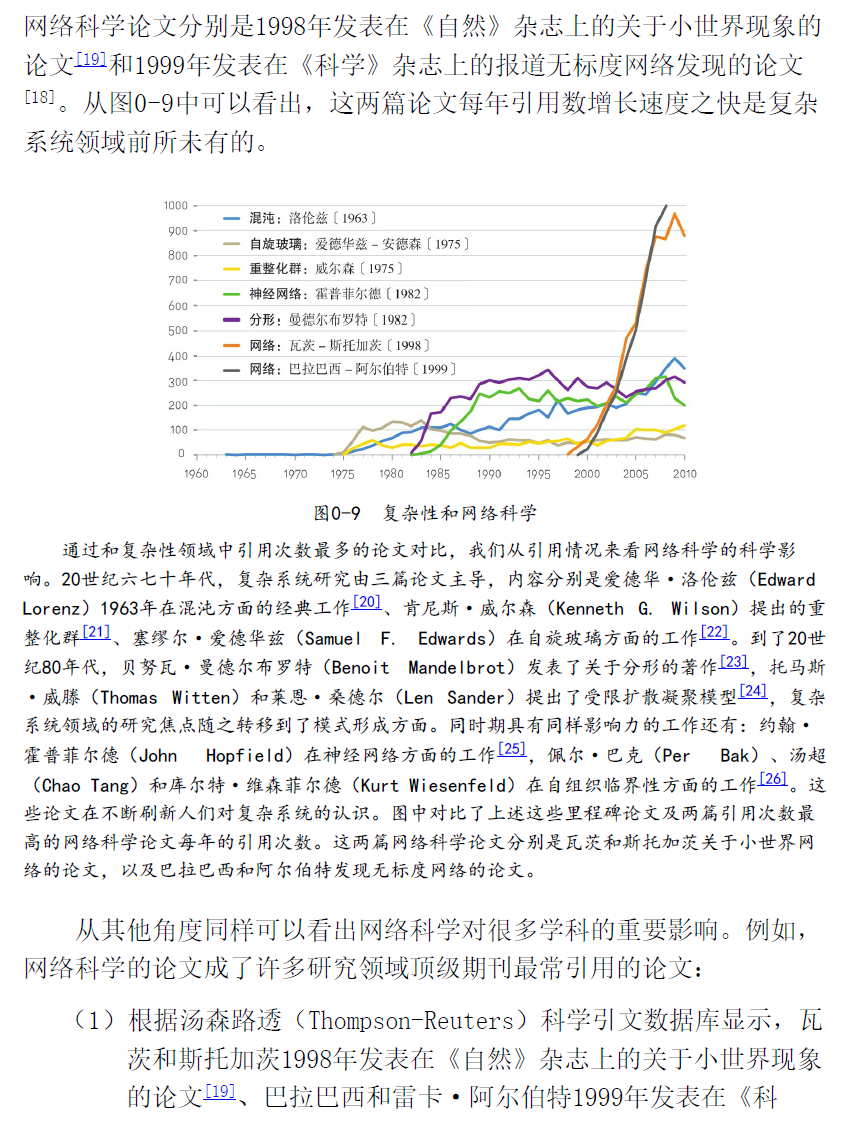




定义与符号
- 引入图论
Graph的知识加以应用,包括无向图undirected graph、有向图directed graph和加权图weighted graph。任何一种网络都是点和边构成,在形式上用无向图G=(N,L)表示,其中N不为空,表示所有节点集合,L表示所有边的集合,通过边连接的两个节点互称为最近邻邻居。 - 加权网络
G=(N,L,W)由三元组表示,W为权值集合。 - 大小为N的图,最少边为0,最多边为
N*(N-1)/2,也就是完全图。如果边数K<<N*N,则为稀疏图。
度与度分布
- 度:与该节点连接的其他节点数目。有向图中,其他节点指向该节点的度叫做入度,该节点指向其他节点叫做出度。
- 网络的平均度:网络中所有节点i和度$$k_i$$的平均值,即$$<k>= \frac{1}{N} \sum_{i=1}^N k_i $$
- 网络中节点度的分布情况可以用分布函数
P(k)来描述,P(k)表示在网络中随机选定一个节点,该节点恰好为K的概率,对于有向网络,需要分别计算连入到节点的入度分布$$P_{in}(K)$$和从节点连出的出度分布$$P_{out}(K)$$两种。 - 为了刻画一个网络中的连接度是如何在节点上进行分布的,一般具有两种方法,一是直接画出
P(K)的分布状态,二是计算度分布的矩(moment)。P(K)的n阶矩定义如下:$$<K^n>=\sum_k K^n P(k)$$,其中一阶矩$$<k>$$对应于网络的平均连接度,二阶矩$$<K^{2}>$$刻画节点连接度分布的波动大小。已有研究表明二阶矩$$<K^2>$$的发散与否将会根本性地影响到网络上发生的动力学过程。
平均路径长度
- 在无向、无权的网络中,两个节点i和j之间的路径长度$$d_{i,j}$$定义为连接这两个节点的最短路径上的边数。网络中任意两个节点之间的距离的最大值称为网络的直径
(diameter),记为D,即$$D=max_{i,j}(d_{i,j})$$ - 网络的平均路径长度
L是对网络中任意两个节点之间的距离求平均值,即为$$L=\frac{1}{N(N-1)\frac{1}{2}}\sum_{i\ge j}d_{i,j}$$ - 网络的平均路径长度也称为网络的特征路径长度
(characteristic path length) - 在大多实际网络中,尽管节点数量通常很大,但网络的平均路径长度却很小。如果给定网络节点平均度$$<K>$$,平均路径长度
L的增加速度至多与网络规模N的对数成正比,则称这个网络具有小世界(small-world)效应。
集聚系数
- 网络中的一个集团是指由一系列的点组合的一个集合,其中的任一个点和该集合中的其它点都连通。聚集系数是指网络集团化的程度,即考察连接在一起的集团各自的近邻之中由多少是共同的近邻。网络的集聚系数的定义为与网络中的任意一点相连的点也彼此相连的平均概率。
- 假设网络中某一个节点
i有$$k_i$$个最近邻,那么在这些最近邻中最多可能存在$$k_i(k_i-1)/2$$条连接。用$$E_i$$表示这些最近邻的点之间实际存在的连接数,则节点i的集群系数定义为:$$C_i=\frac{E_i}{k_i(k_i-1)/2}=\frac{2E_i}{k_i(k_i-1)}$$ - 整个网络的集聚系数
C就是所有节点i的聚集系数$$C_i$$的平均值,$$C=\frac{1}{N}\sum_{i=1}^NC_i$$,它描述了网络中节点与节点集结成团的趋势。 - 规则网络具有较大的集聚系数和较大的平均路径长度。

连通性

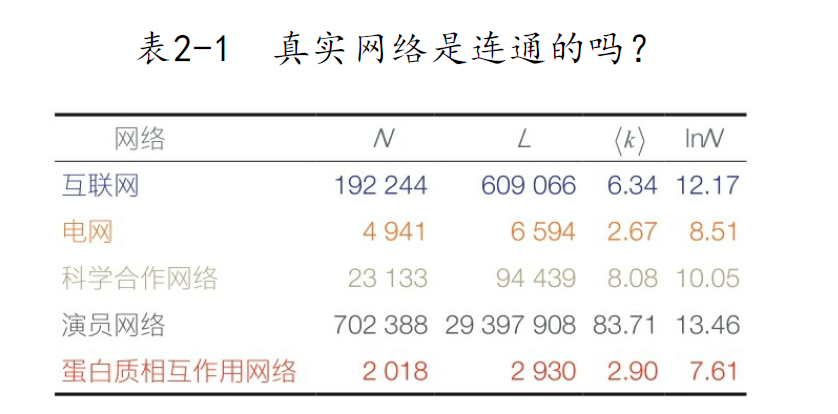
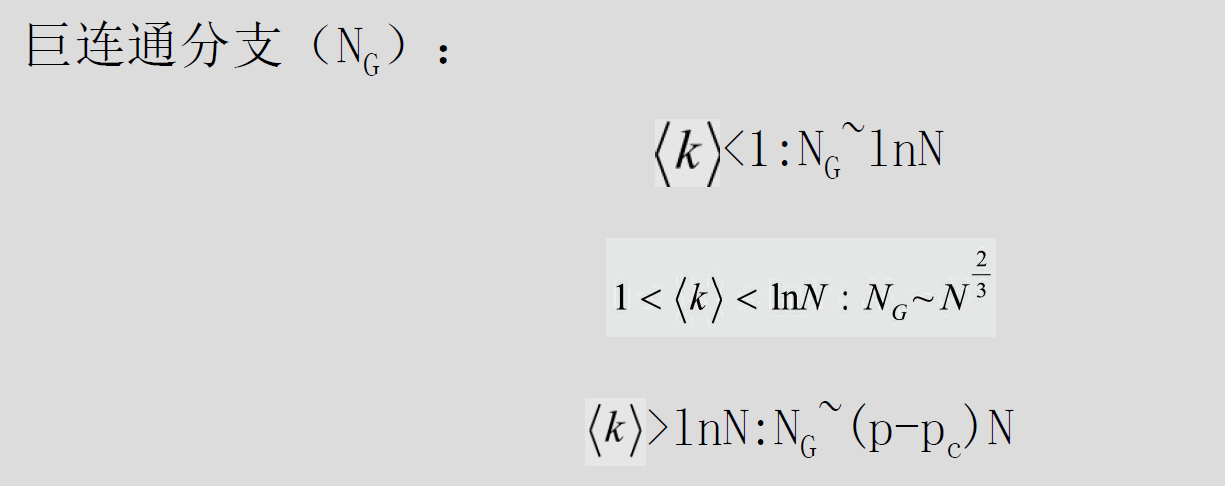
- 连通性:只要网络中每个节点都存在最短路径,即网络是连通的。
入门任务
链和环链
- 生成任意节点一维链
module network
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N)
implicit none
integer :: N
integer :: i,j,number
integer,allocatable :: chain_matrix(:,:)
allocate(chain_matrix(N,N))
!初始化网络矩阵
chain_matrix=0
!赋值节点关系
do i=1,N-1,1
chain_matrix(i,i+1)=1
chain_matrix(i+1,i)=1
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') chain_matrix(i,j)
end do
write(10,*)
end do
deallocate(chain_matrix)
end subroutine sub
end module network
program main
use network
implicit none
integer :: N !节点数量
open(fileid,file='chain.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
call sub(N)
stop
end program main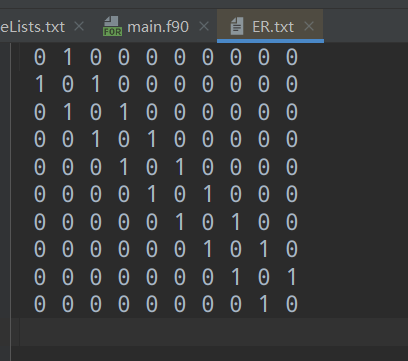
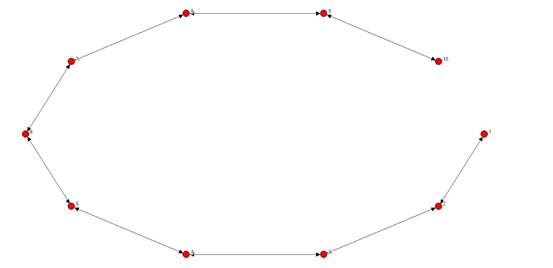
- 生成任意节点环链
module network
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N)
implicit none
integer :: N
integer :: i,j,number
integer,allocatable :: ring_matrix(:,:)
allocate(ring_matrix(N,N))
!初始化网络矩阵
ring_matrix=0
!赋值节点关系
do i=1,N-1,1
ring_matrix(i,i+1)=1
ring_matrix(i+1,i)=1
end do
!首位相连
ring_matrix(N,1)=1
ring_matrix(1,N)=1
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') ring_matrix(i,j)
end do
write(10,*)
end do
deallocate(ring_matrix)
end subroutine network
end module ER
program main
use network
implicit none
integer :: N !节点数量
open(fileid,file='ER.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
call sub(N)
stop
end program main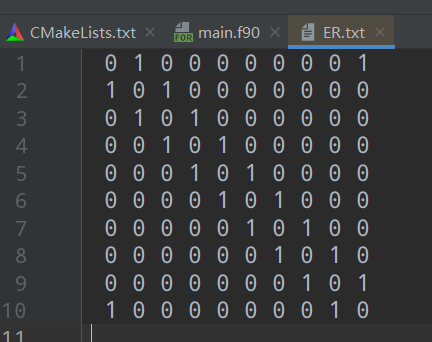
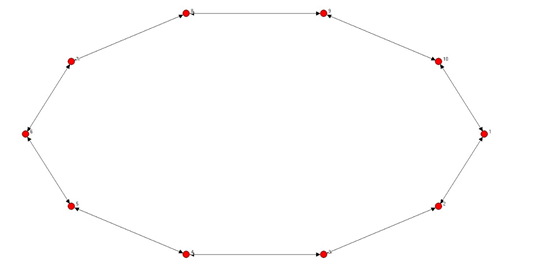
常见网络
完全连接网络
- 要求:节点与其他节点都有连接
module ER
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N)
implicit none
integer :: N
integer :: i,j,number
integer,allocatable :: ER_matrix(:,:)
allocate(ER_matrix(N,N))
!初始化网络矩阵
ER_matrix=0
!赋值节点关系,定义完全图矩阵
do i=1,N-1,1
do j=1,N-i,1
ER_matrix(j,j+i)=1
ER_matrix(j+i,j)=1
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') ER_matrix(i,j)
end do
write(10,*)
end do
deallocate(ER_matrix)
end subroutine sub
end module ER
program main
use ER
implicit none
integer :: N !节点数量
open(fileid,file='ER.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
call sub(N)
stop
end program main

最近邻居连接
- 一个节点与左右连,还与左右的左右连
module ER
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N)
implicit none
integer :: N
integer :: i,j,number
integer,allocatable :: ER_matrix(:,:)
allocate(ER_matrix(N,N))
!初始化网络矩阵
ER_matrix=0
!赋值节点关系,定义最近邻居图矩阵,先连环,再连邻居
do i=1,N-1,1
ER_matrix(i,i+1)=1
ER_matrix(i+1,i)=1
end do
do i=1,N-2,1
ER_matrix(i,i+2)=1
ER_matrix(i+2,i)=1
end do
ER_matrix(1,N-1)=1
ER_matrix(2,N)=1
ER_matrix(N-1,1)=1
ER_matrix(N,2)=1
!定义环
ER_matrix(1,N)=1
ER_matrix(N,1)=1
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') ER_matrix(i,j)
end do
write(10,*)
end do
deallocate(ER_matrix)
end subroutine sub
end module ER
program main
use ER
implicit none
integer :: N !节点数量
open(fileid,file='ER.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
call sub(N)
stop
end program main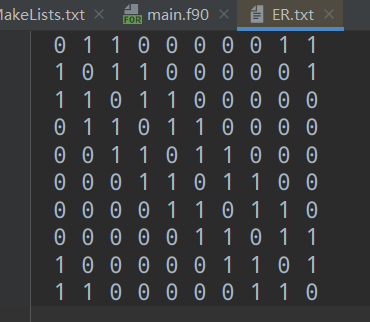

可变邻居链接
K为偶数
- 输入节点数和单节点邻居数
module ER
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N,K)
implicit none
integer :: N,K !单节点K个邻居
integer :: i,j,number
integer,allocatable :: neighbour_matrix(:,:)
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
!赋值节点关系
!方法一:定义最近邻居图矩阵,先连环,再连邻居
!连始点右邻居
! do j=1,K/2,1
! do i=1,N-j,1
! neighbour_matrix(i,i+j)=1
! neighbour_matrix(i+j,i)=1
! end do
! end do
! !连始点左邻居
! do j=1,K/2,1
! do i=N-K/2+j,N,1
! neighbour_matrix(j,i)=1
! neighbour_matrix(i,j)=1
! end do
! end do
!方法二:分析可知:邻边矩阵对应|i-j|>=N-K/2或者|i-j|<=K/2
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
deallocate(neighbour_matrix)
end subroutine sub
end module ER
program main
use ER
implicit none
integer :: N,K !N节点数量,K邻居数
open(fileid,file='matrix.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "请输入单节点邻居总数:"
read(*,*) K
call sub(N,K)
stop
end program main
- N=20,K=8
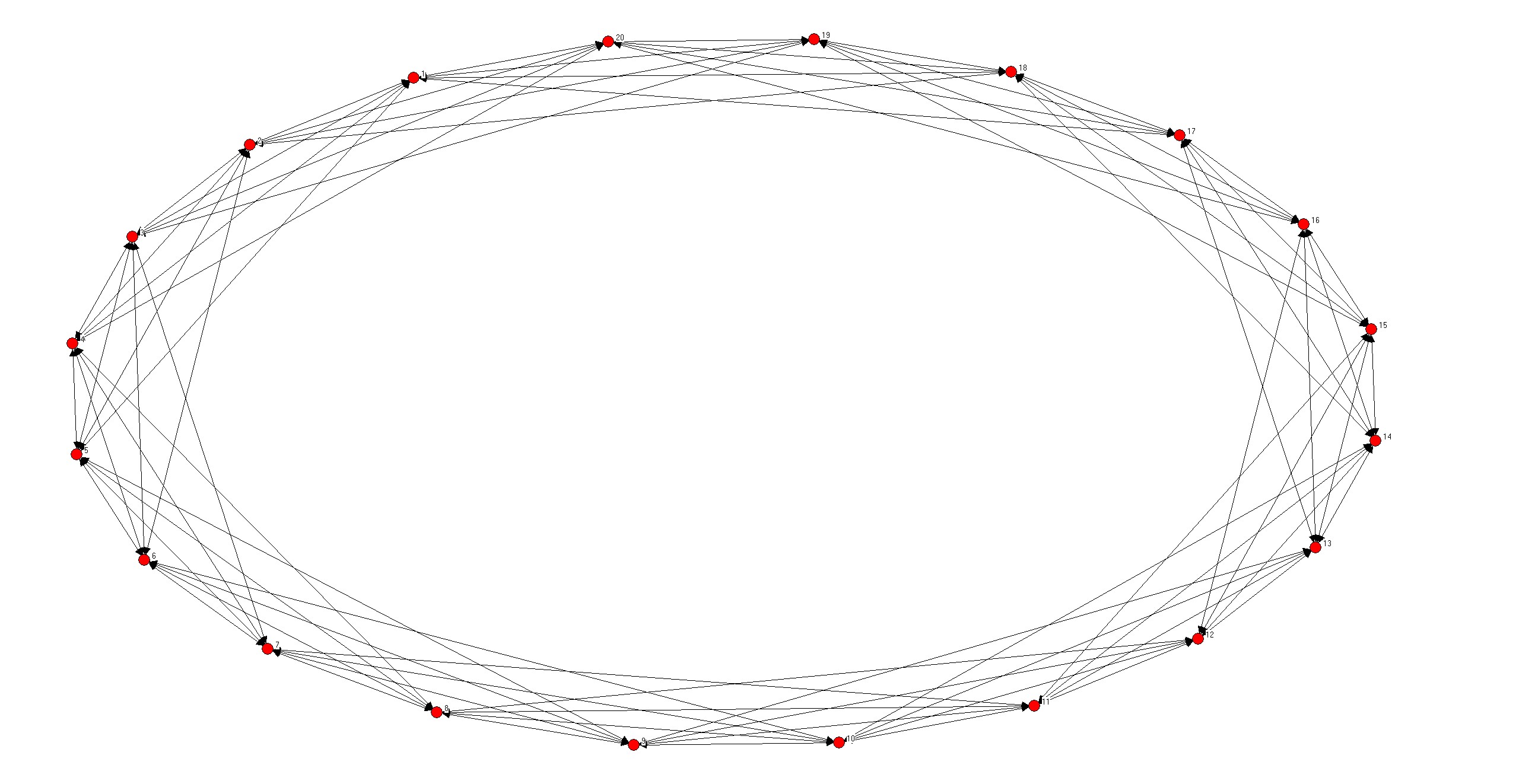
K为奇数
module ER
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N,K)
implicit none
integer :: N,K !单节点K个邻居
integer :: i,j,number
integer,allocatable :: neighbour_matrix(:,:)
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
if(mod(N,2)/=0) then
write(*,*) "节点为奇数,请输入偶数节点"
stop
end if
!赋值节点关系
!分析可知:邻边矩阵对应|i-j|>=N-K/2或者|i-j|<=K/2
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2.or.abs(i-j)==N/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
deallocate(neighbour_matrix)
end subroutine sub
end module ER
program main
use ER
implicit none
integer :: N,K !N节点数量,K邻居数
open(fileid,file='matrix.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "请输入单节点邻居总数:"
read(*,*) K
call sub(N,K)
stop
end program main

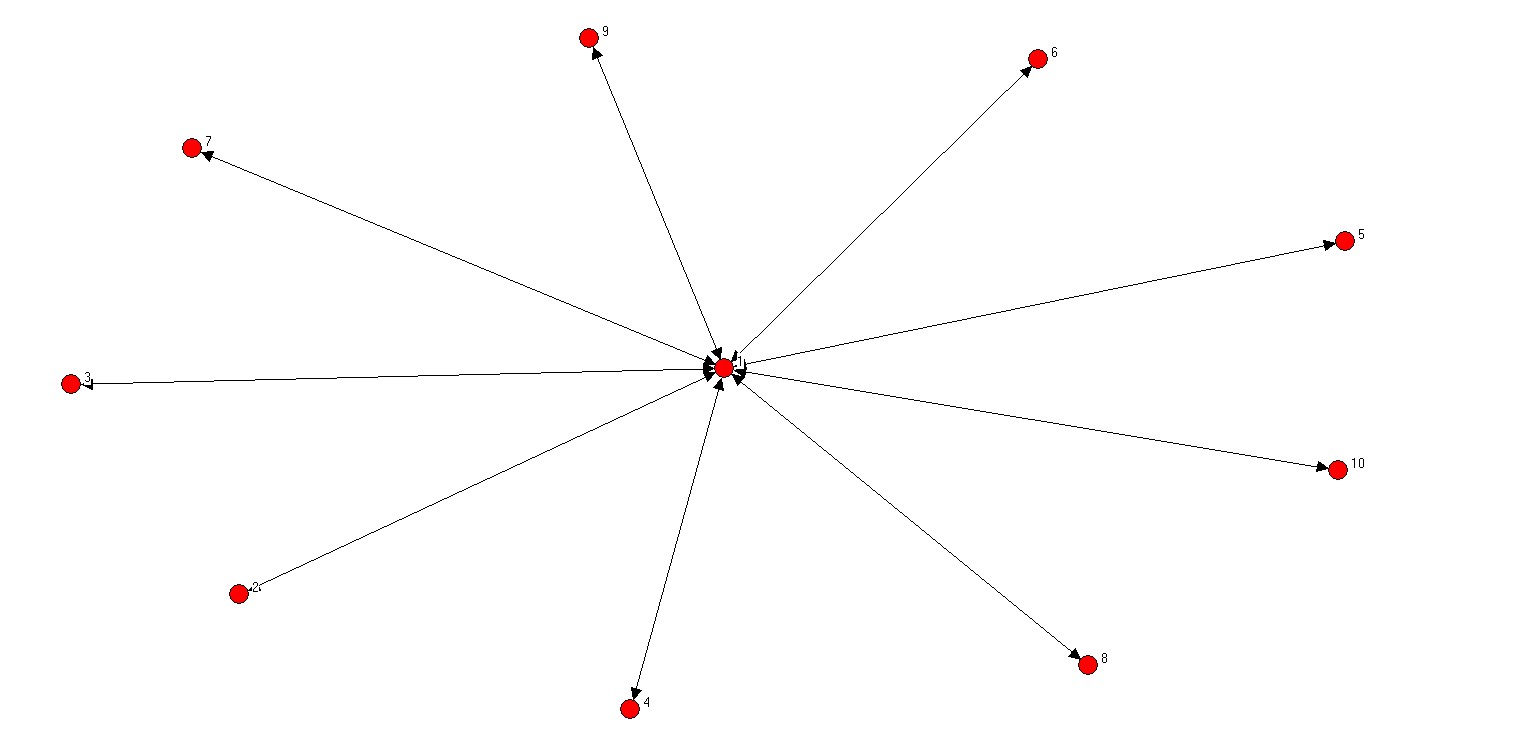
星形链接图
- 要求:一个节点与其它节点都相连
- 实现过程,只要每行及对应列除对角线上的节点为0,其它为1即可。
module ER
implicit none
integer,parameter :: fileid=10
contains
subroutine sub(N)
implicit none
integer :: N
integer :: i,j,number
integer,allocatable :: ER_matrix(:,:)
allocate(ER_matrix(N,N))
!初始化网络矩阵
ER_matrix=0
!赋值节点关系,定义星形连接矩阵
do i=2,N,1
ER_matrix(1,i)=1
ER_matrix(i,1)=1
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') ER_matrix(i,j)
end do
write(10,*)
end do
deallocate(ER_matrix)
end subroutine sub
end module ER
program main
use ER
implicit none
integer :: N !节点数量
open(fileid,file='ER.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
call sub(N)
stop
end program main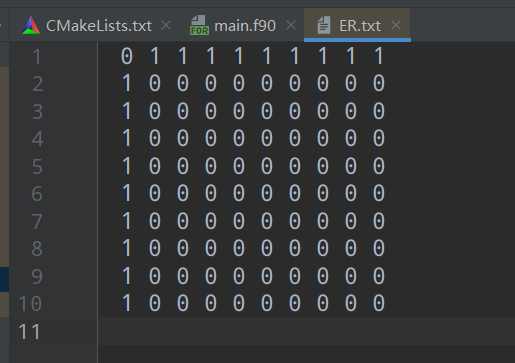
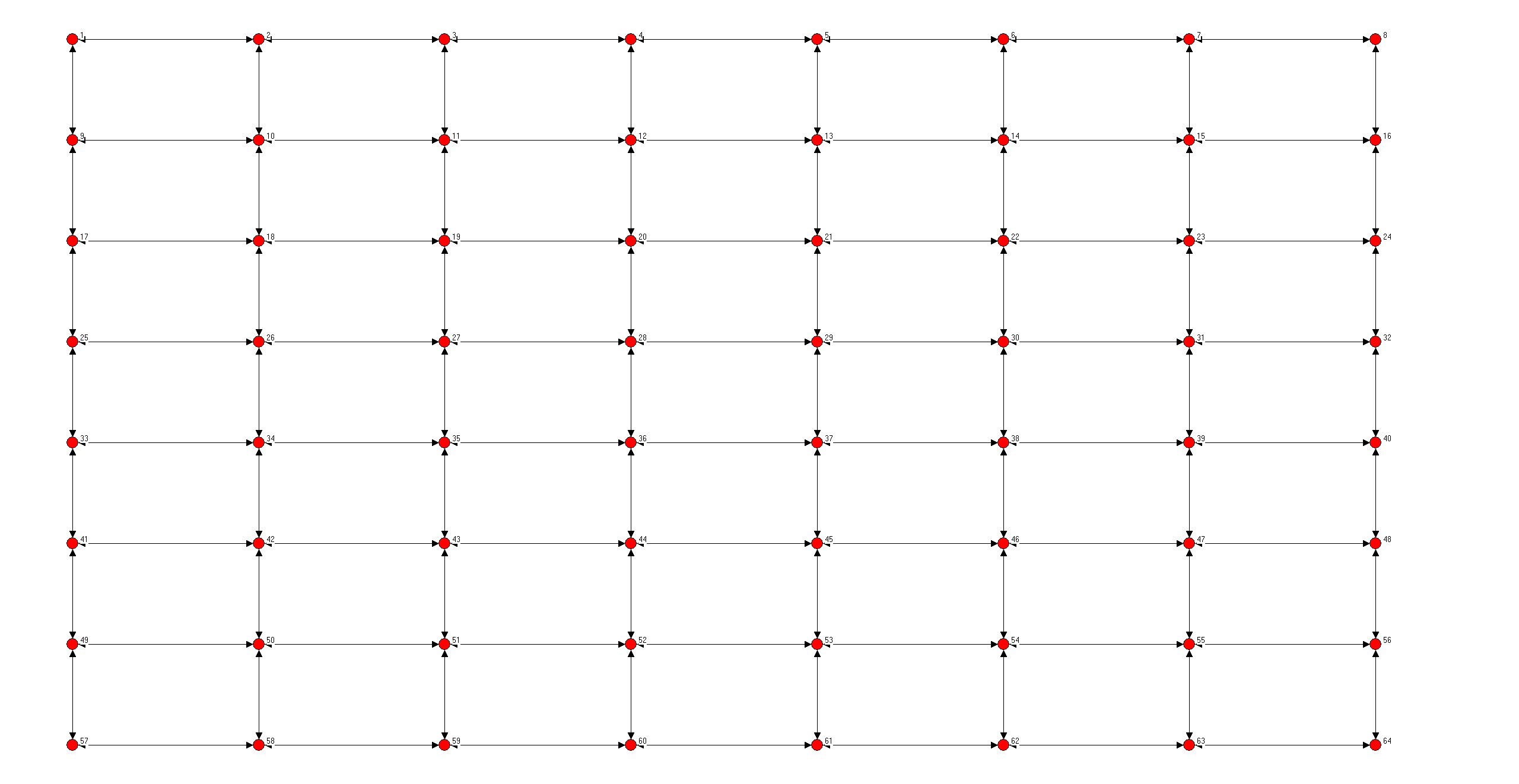
二维网格
- 要求:网格线排布
- 实现过程:根据列数断行,先连行,再连列。
module draw
implicit none
integer,parameter :: fileid = 10
contains
subroutine sub1(N,a,b)
implicit none
integer :: N
integer :: i,j,number
integer :: a,b !创建a行b列的网格
integer,allocatable :: grid_matrix(:,:)
allocate(grid_matrix(N,N))
!初始化网络矩阵
grid_matrix=0
!赋值节点关系
a = N/b !可要可不要,这里可以判断节点数量是否构成网格
do i=1,N-1,1
grid_matrix(i,i+1)=1
grid_matrix(i+1,i)=1
end do
do i=b,N-1,b !拆链成行
grid_matrix(i,i+1)=0
grid_matrix(i+1,i)=0
do j=1,N-b,1 !连行成列
grid_matrix(j,j+b)=1
grid_matrix(j+b,j)=1
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(10,"(I2)",advance='no') grid_matrix(i,j)
end do
write(10,*)
end do
deallocate(grid_matrix)
end subroutine sub1
end module draw
program drawGrid
use draw
implicit none
integer :: N
integer :: a,b
write(*,*) "请输入网络节点数:"
read(*,*) N
write(*,*) "请输入网格行、列数:"
read(*,*) a,b
open(unit=fileid,file="matrix.txt")
call sub1(N,a,b)
stop
end program
ER随机网络模型
Erdos-Renyi network(ER)实现:产生随机数,大于阈值则赋值为1,小于阈值则赋值为0
module ER
implicit none
integer,parameter :: fileid1=10,fileid2=20,fileid3=30,fileid4=40,fileid5=50,Infinity=10000!Infinity代替无穷大
integer,allocatable :: ER_matrix(:,:)
integer,allocatable :: degree(:),E(:)
real,allocatable :: C(:)
integer :: N
common N
contains
subroutine sub(N,P)
implicit none
integer :: N,i,j,a,b
real :: x,P
allocate(ER_matrix(N,N))
!初始化网络矩阵
ER_matrix=0
!赋值节点关系,随机判断
call random_seed()
do i=N,2,-1
do j=i-1,1,-1
!产生随机数
call random_number(x)
if(x<p) then
ER_matrix(j,i)=1
ER_matrix(i,j)=1
end if
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(fileid1,"(I2)",advance='no') ER_matrix(i,j)
end do
write(fileid1,*)
end do
close(fileid1)
end subroutine sub
!degree度
subroutine node_degree()
implicit none
integer :: i,j,number
allocate(degree(N))
do i=1,N,1
number=0
do j=1,N,1
if(ER_matrix(i,j)==1) then
number=number+1
end if
end do
degree(i)=number
write(fileid2,*) i,number
end do
close(fileid2)
end subroutine node_degree
!distribution,度分布
subroutine distribution()
implicit none
integer :: i,j,number1,max_degree=0,min_degree=10000000
!找到最大值、最小值
do i=1,N,1
if(max_degree<degree(i)) then
max_degree=degree(i)
end if
if(min_degree>degree(i)) then
min_degree=degree(i)
end if
end do
!统计度分布
if(min_degree==max_degree) then
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
else
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
end if
close(fileid3)
end subroutine distribution
!集聚系数Clustering coefficient
subroutine Concentration()
implicit none
real :: C_average=0.0
integer :: i,j,a,number2
allocate(E(N))
allocate(C(N))
!Ci=2*E(i)/[K(i)*(K(i)-1)]
E=0
do i=1,N,1
number2=0
do j=1,N,1
if(ER_matrix(i,j)==1) then
do a=1,N,1
if(i/=a) then
if(ER_matrix(a,j)==1.and.ER_matrix(i,a)==1) then
number2=number2+1
end if
end if
end do
end if
end do
E(i)=number2/2 !E(i)为节点邻居的所有连边数
end do
C=0.0
do i=1,N,1
if(degree(i)-1<=0.or.degree(i)==0) then
C(i)=0.0
else
C(i)=2.0*E(i)/(degree(i)*(degree(i)-1))
end if
write(fileid4,*) i,C(i)
C_average=C_average+C(i)
end do
C_average=C_average/N !聚集系数C
write(*,*) "C=",C_average
close(fileid4)
end subroutine Concentration
!最短路径长度
subroutine shortPath(node1,node2)
implicit none
integer :: node1,node2 !两个节点
integer :: i,j,a,b
real :: sum_path=0,L
logical :: status=.true. !true表示网络连通
integer,allocatable :: P(:,:),ER_matrix_path(:,:),sequence(:)
allocate(ER_matrix_path(N,N))
allocate(P(N,N))
allocate(sequence(N))
ER_matrix_path=ER_matrix
P=0
sequence=0
!生成节点路径大小矩阵
do i=1,N-1,1
do j=i+1,N,1
if(ER_matrix_path(i,j)==0) then
ER_matrix_path(i,j)=Infinity
ER_matrix_path(j,i)=Infinity
end if
end do
end do
if(node1<=N.and.node2<=N.and.node1/=node2) then
!广度优先遍历,使用Floyd算法
do a=1,N,1
do i=1,N-1,1
do j=i+1,N,1
if(ER_matrix_path(i,j)>ER_matrix_path(i,a)+ER_matrix_path(a,j)) then
ER_matrix_path(i,j)=ER_matrix_path(i,a)+ER_matrix_path(a,j)
ER_matrix_path(j,i)=ER_matrix_path(i,a)+ER_matrix_path(a,j)
P(i,j)=a
end if
end do
end do
end do
!输出节点路径大小矩阵,及最短路径矩阵
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') ER_matrix_path(i,j)
end do
write(fileid5,*)
end do
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') P(i,j)
end do
write(fileid5,*)
end do
if(ER_matrix_path(node1,node2)==Infinity) then
write(*,*) node1,node2,"不存在路径"
else
write(*,*) "节点",node1,"和节点",node2,"的最短路径为:",ER_matrix_path(node1,node2)
end if
else
write(*,*) "输入节点错误!"
end if
close(fileid5)
!平均路径长度,L=1/(N*(N-1))*累加(d(i,j))
do i=1,N-1,1
do j=i+1,N,1
if(ER_matrix_path(i,j)/=Infinity) then
sum_path=sum_path+ER_matrix_path(i,j)
else
status = .false.
end if
end do
end do
L=sum_path/(N*(N-1)/2)
write(*,*) "平均路径长度为:",L
if(status.eqv..true.) then
write(*,*) "网络连通!"
else
write(*,*) "网络不连通!"
end if
deallocate(P)
end subroutine shortPath
end module ER
program main
use ER
implicit none
real :: P !链接概率0~1
integer :: node1,node2 !两个节点
open(fileid1,file='ER.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "请输入节点对链接概率:"
read(*,*) P
call sub(N,P)
open(fileid2,file='degree.txt')
call node_degree()
write(*,*) "节点__度 数据生成完毕"
open(fileid3,file='distribution.txt')
call distribution()
write(*,*) "度__数量 数据生成完毕"
open(fileid4,file='Concentration.txt')
write(*,*) "集聚系数:"
call Concentration()
open(fileid5,file='shortPath.txt')
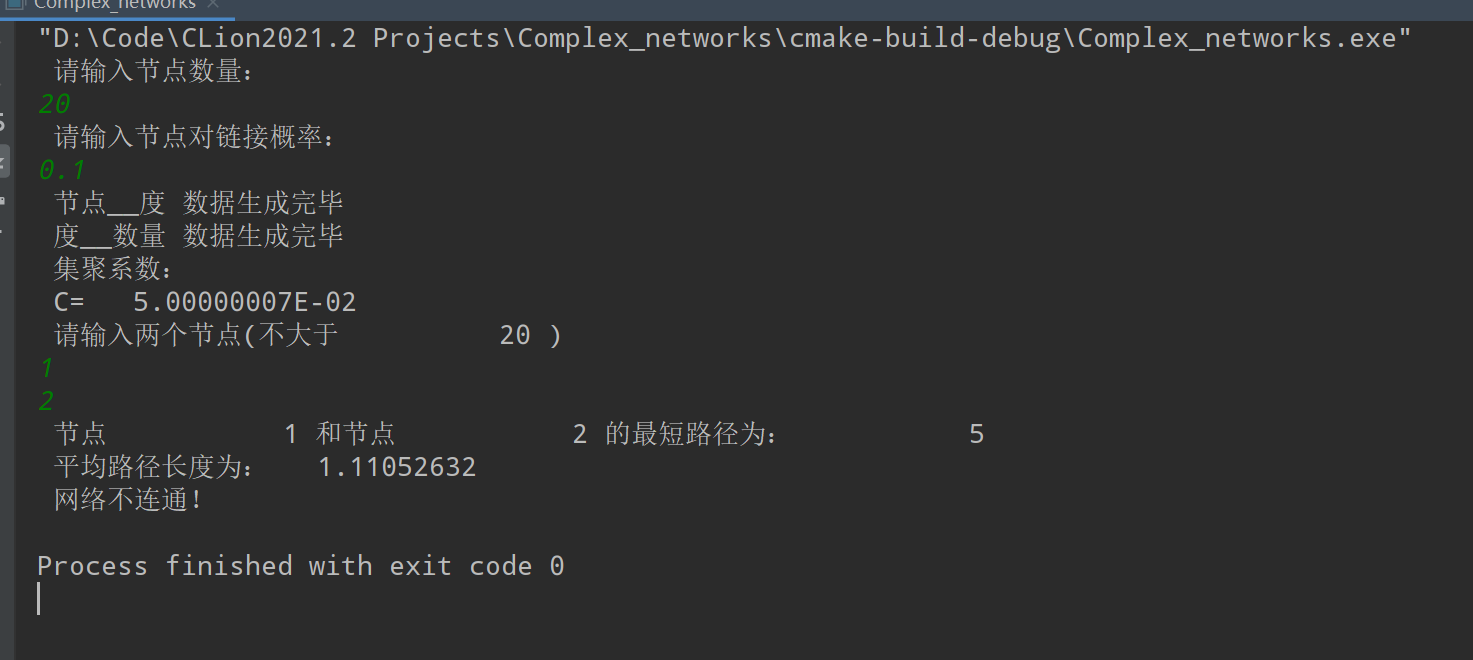
write(*,*) "请输入两个节点(不大于",N,")"
read(*,*) node1,node2
call shortPath(node1,node2)
deallocate(ER_matrix)
deallocate(degree)
deallocate(E)
deallocate(C)
stop
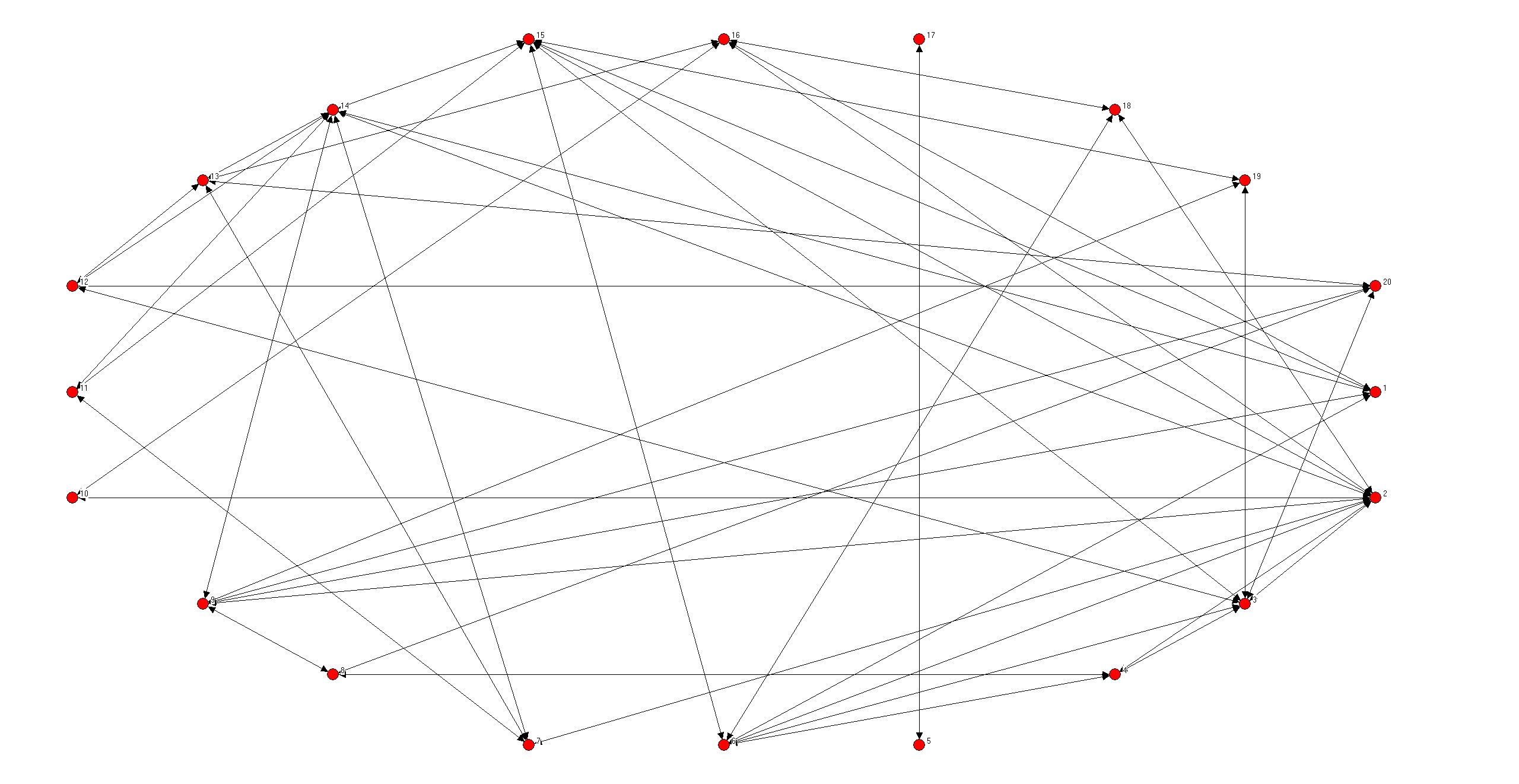
end program main- N=20;P=0.1



- N=20;P=0.3
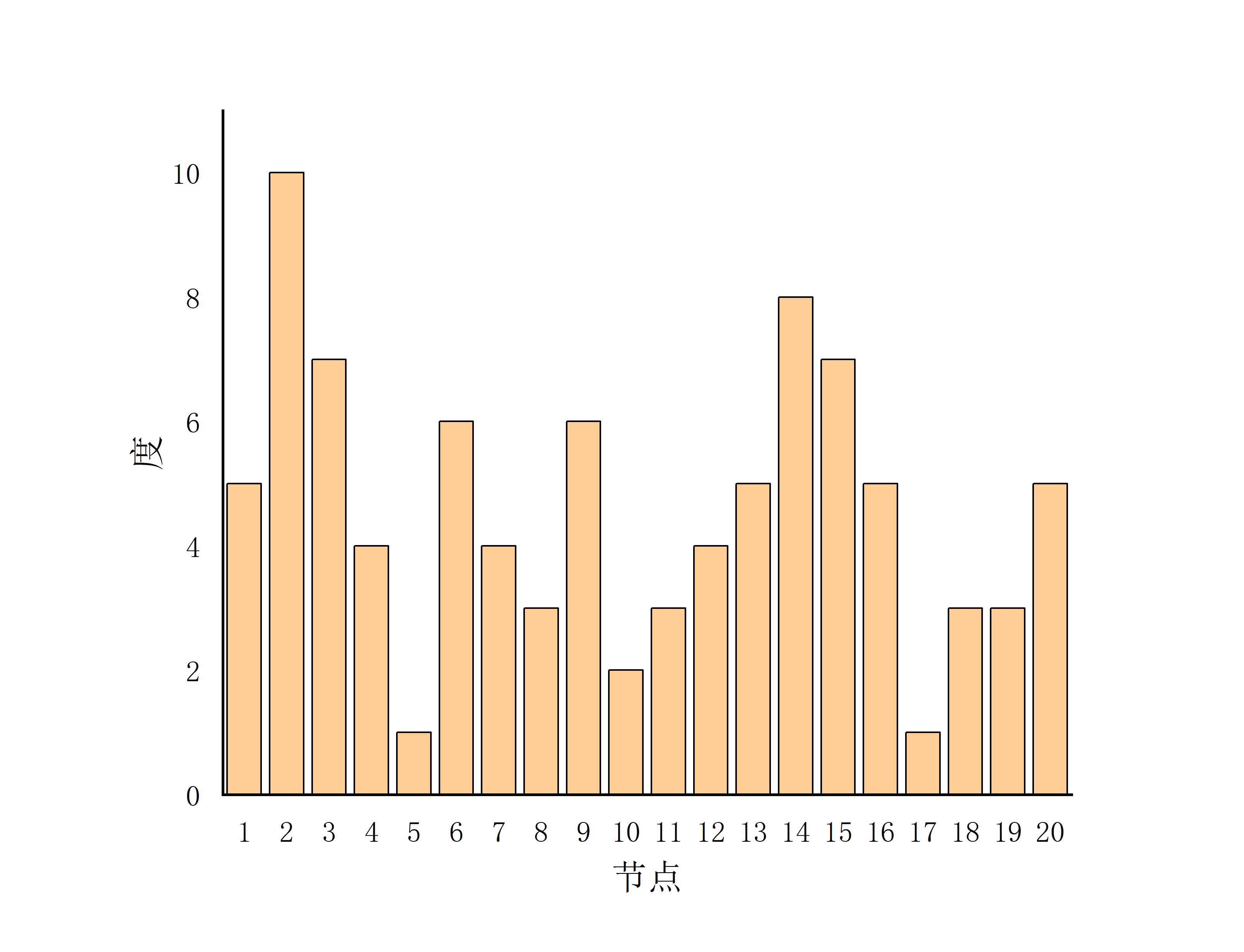


- N=20;P=0.5
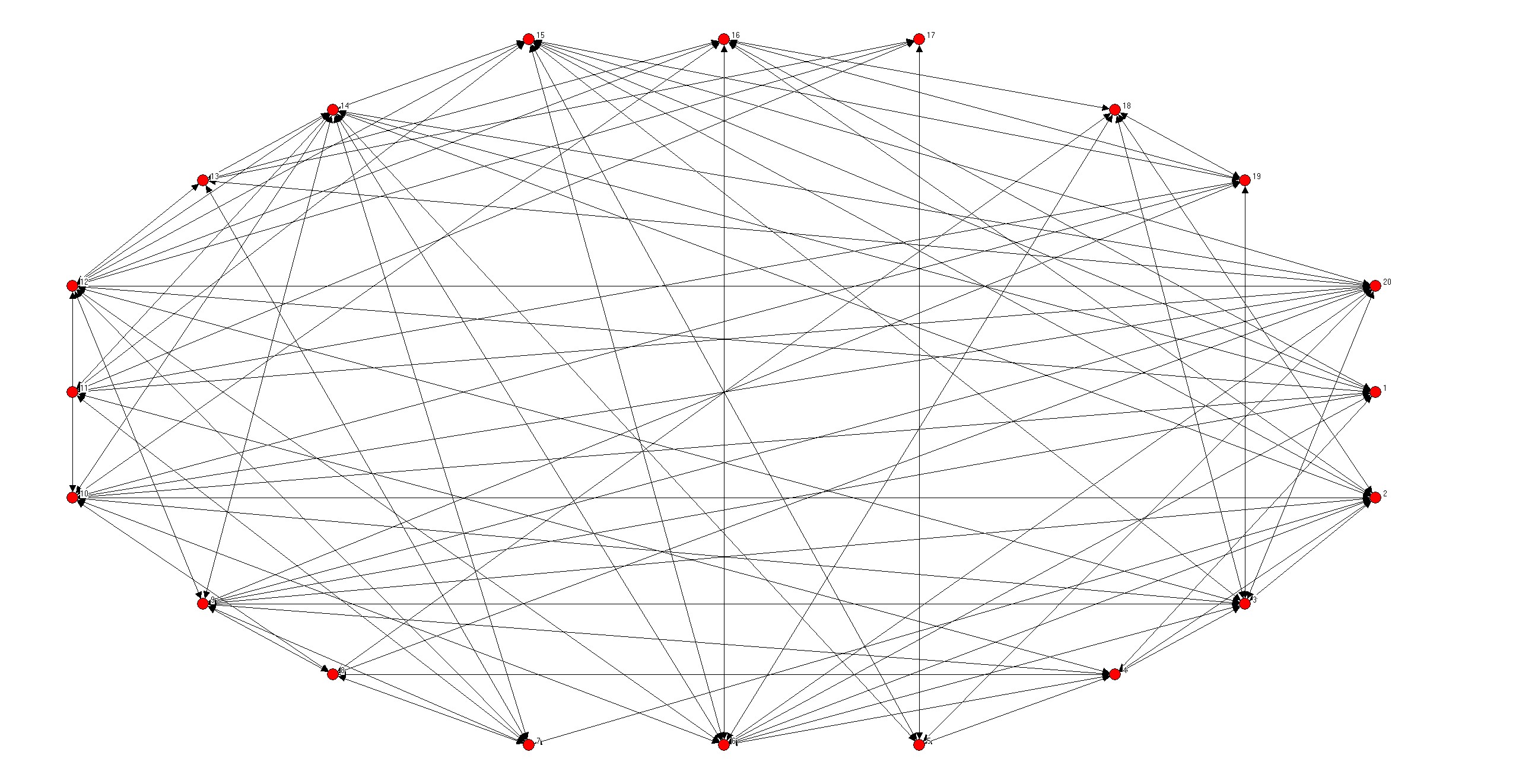
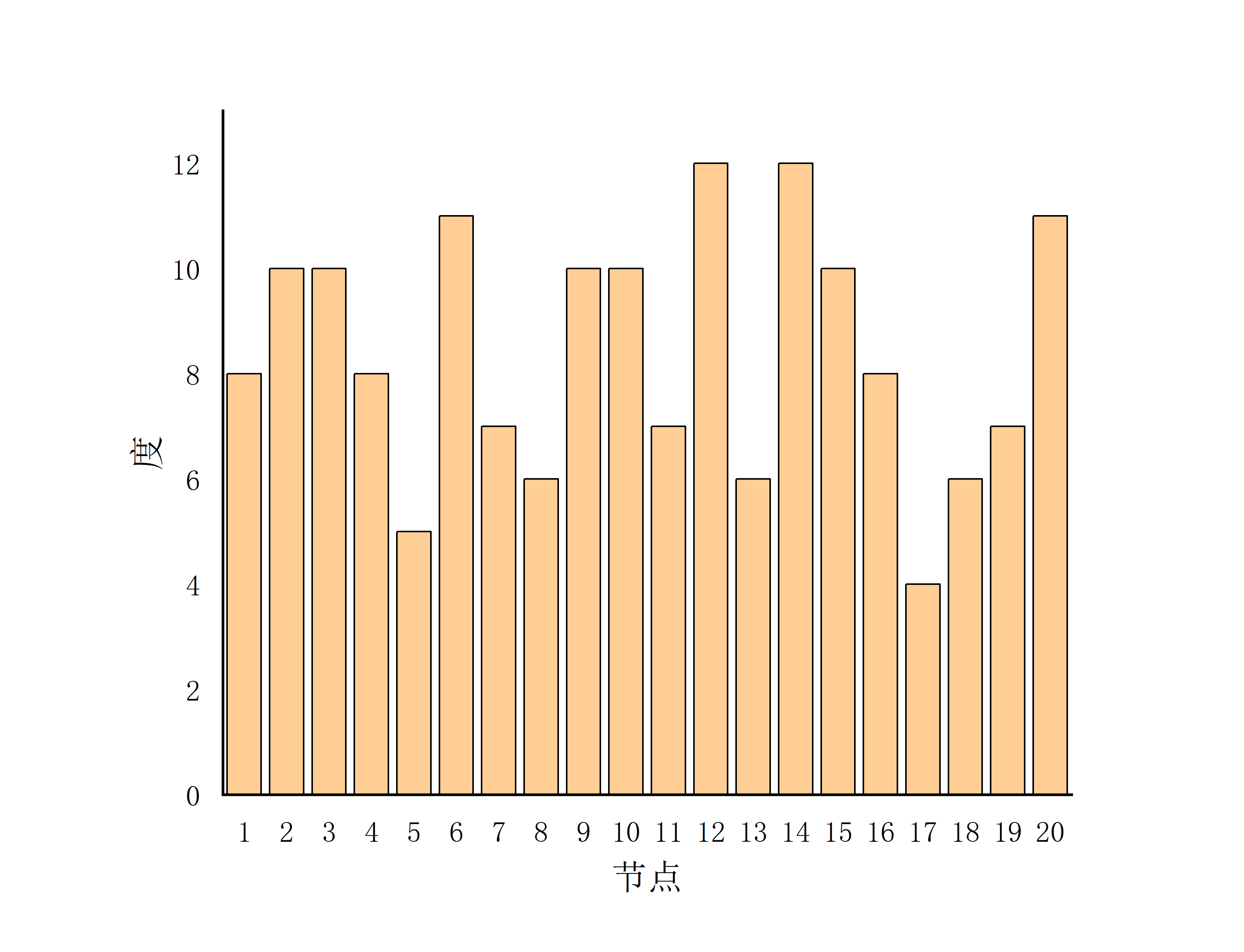


- N=20;P=0.7

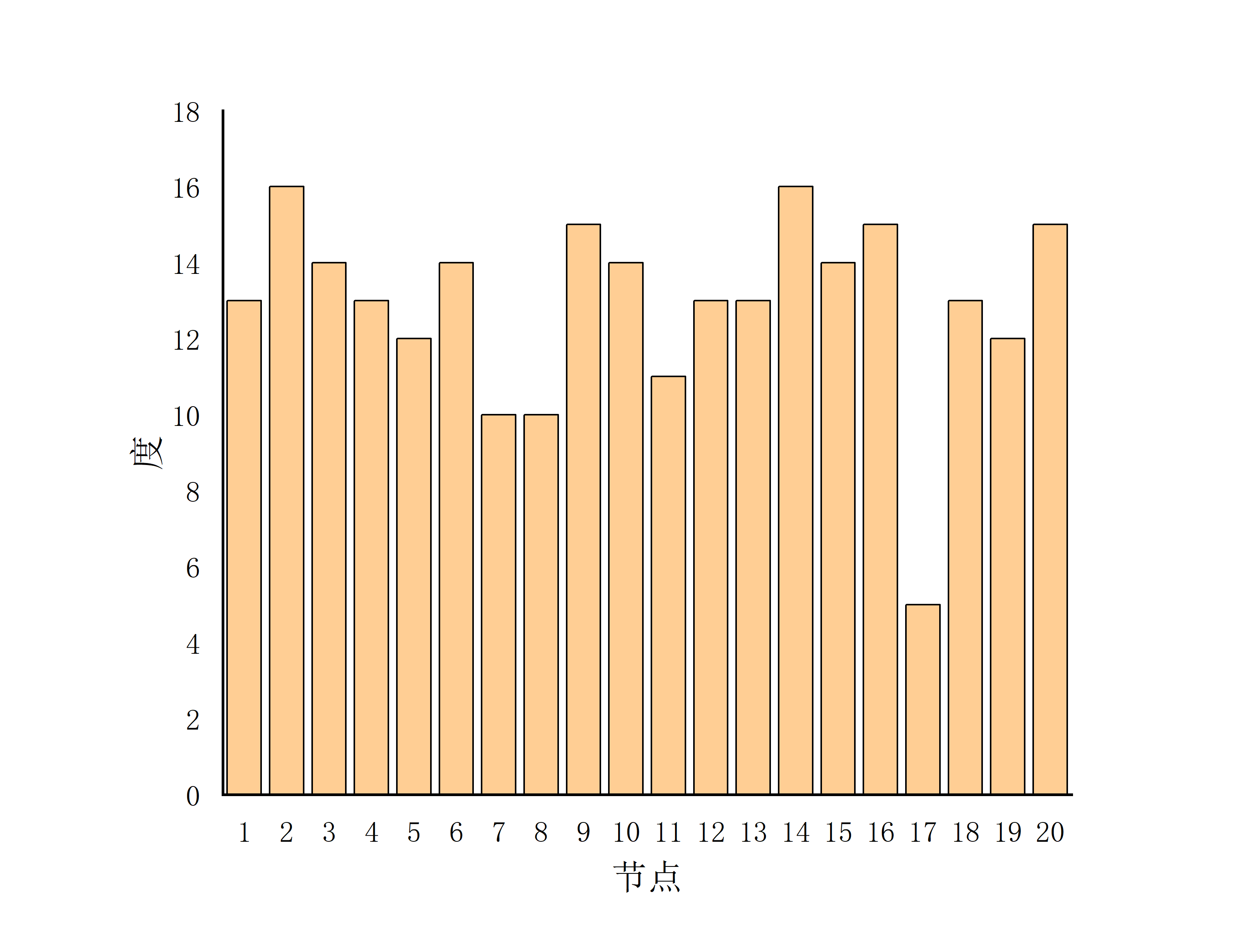
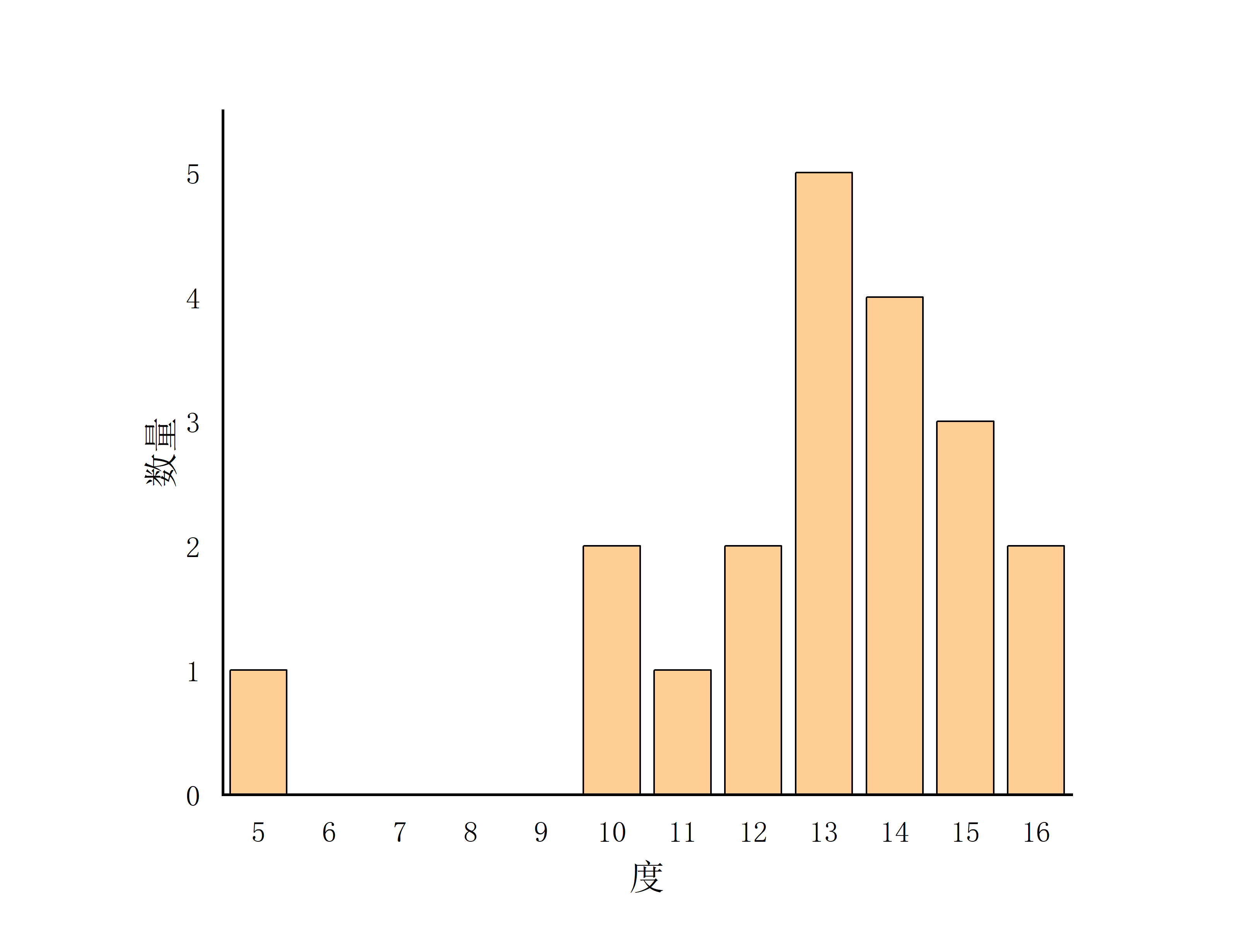
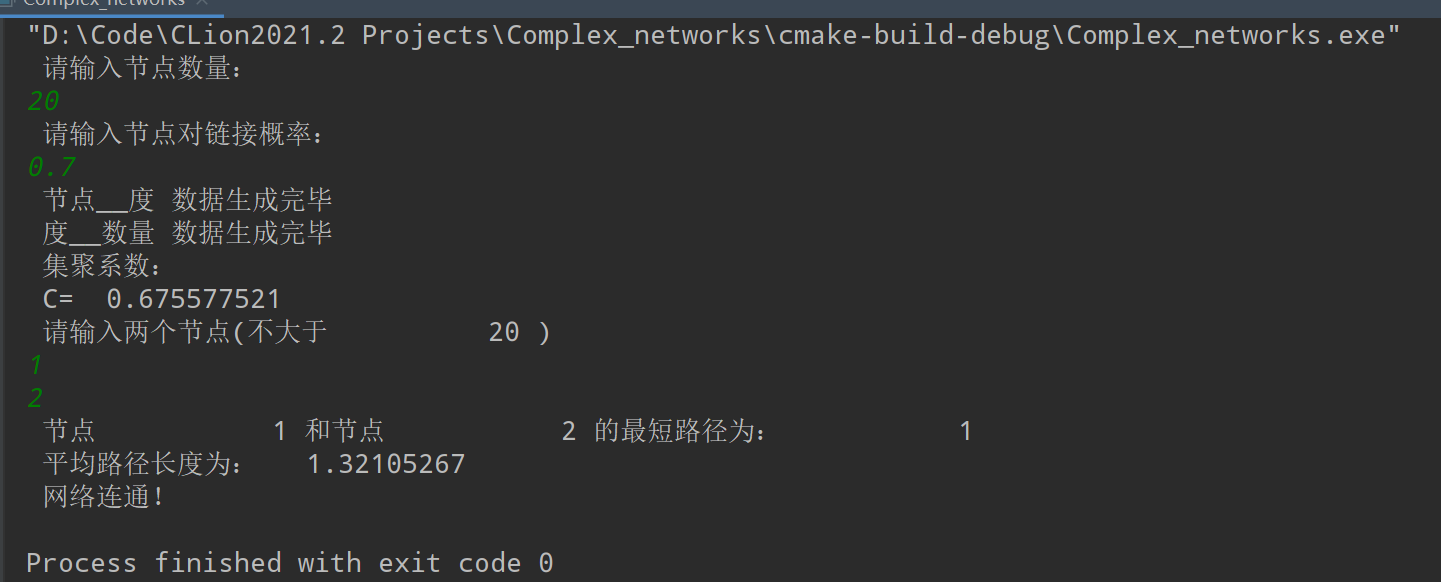
- N=20;P=1
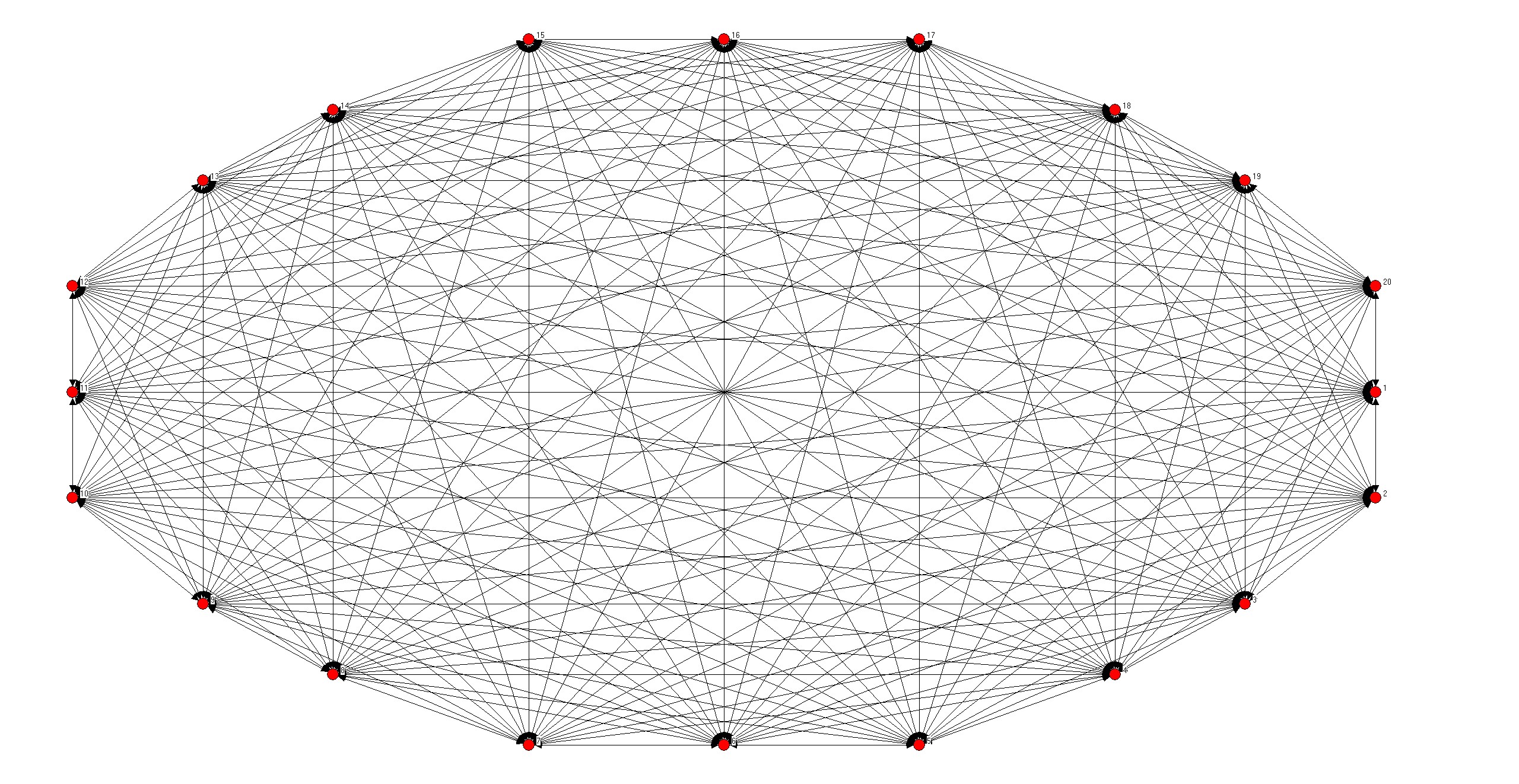
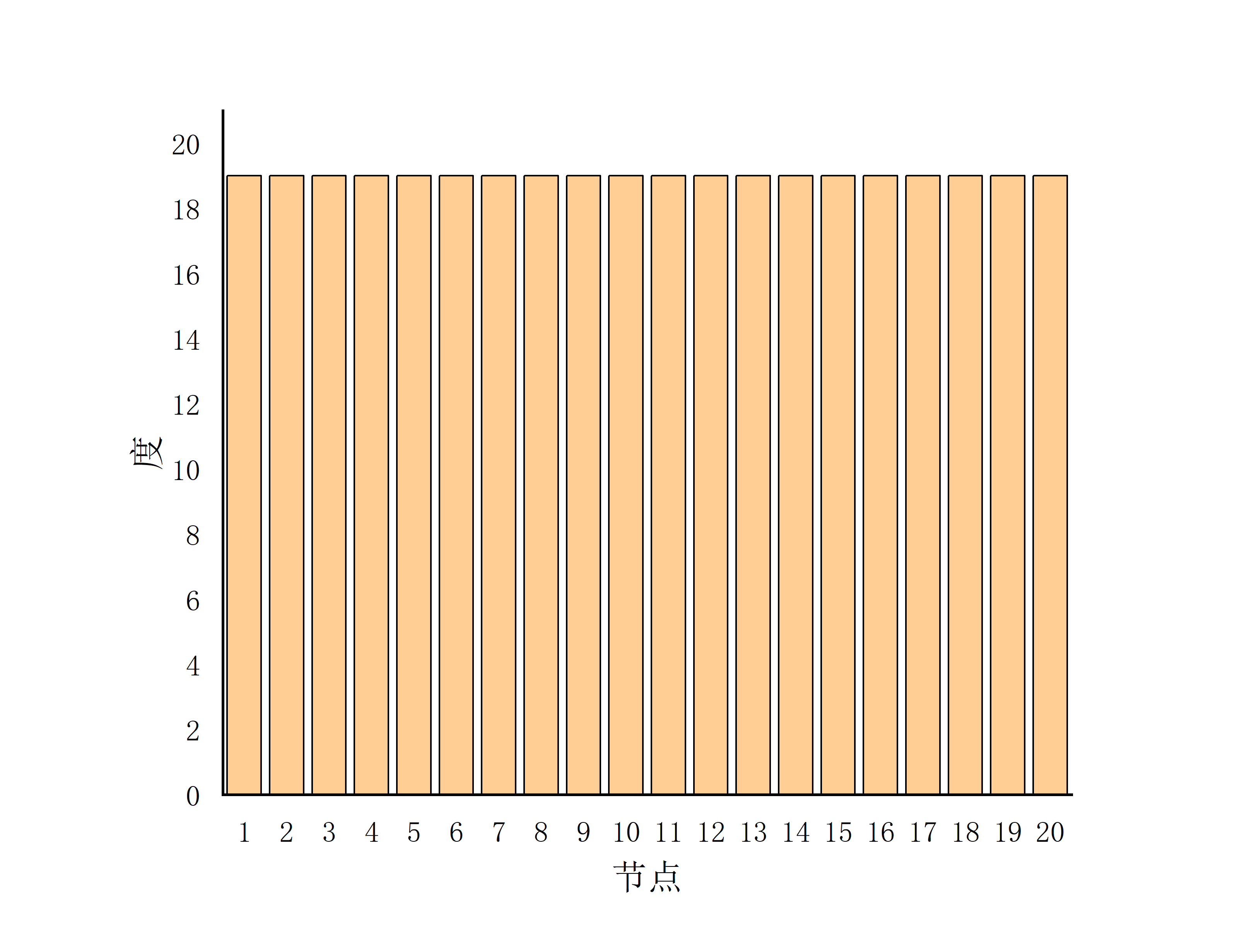



- 基本服从泊松分布(N越大,越接近泊松分布)
均匀随机网络模型
- 均匀随机网络,将度确定的规则网路随机化,保持度不变。
- 需要考虑两种情况,K为奇数时,N必须是偶数,K为偶数时,N不限制奇、偶性

module neighbour
implicit none
integer,parameter :: fileid1=10,fileid2=20,fileid3=30,fileid4=40,fileid5=50,Infinity=10000!Infinity代替无穷大
integer,allocatable :: neighbour_matrix(:,:),degree(:),E(:)
real,allocatable :: C(:)
integer :: N
common N
contains
subroutine sub(N,K)
implicit none
integer :: N,K !单节点K个邻居
integer :: i,j,a,b
real :: x1,x2
integer :: y1,y2
integer,allocatable :: up_matrix(:,:)
allocate(neighbour_matrix(N,N))
allocate(up_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
!赋值节点关系
!分析可知:邻边矩阵对应|i-j|>=N-K/2或者|i-j|<=K/2
if(mod(K,2)==0) then
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
else
if(mod(N,2)/=0) then
write(*,*) "输入K为奇数,请修改N值,使其为偶数"
stop
end if
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2.or.abs(i-j)==N/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
end if
!均匀随机化
!创建随机选择边的范围矩阵
do a=1,N-1,1
do b=a+1,N,1
up_matrix(a,b)=1
end do
end do
call random_seed()
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix(i,j)==1) then
100 call random_number(x1)
y1=nint((x1-0.51/N)*N+1)!取N的概率比其它少0.02
call random_number(x2)
y2=nint((x2-0.51/N)*N+1)!取N的概率比其它少0.02
if(neighbour_matrix(j,y1)==0.and.neighbour_matrix(i,y2)==0.and.j/=y1.and.i/=y2&
&.and.neighbour_matrix(y1,y2)==1.and.up_matrix(y1,y2)==1) then !判断两边断开后,是否可以正确重连
!断边
neighbour_matrix(i,j)=0
neighbour_matrix(j,i)=0
neighbour_matrix(y1,y2)=0
neighbour_matrix(y2,y1)=0
!重连
neighbour_matrix(i,y2)=1
neighbour_matrix(y2,i)=1
neighbour_matrix(j,y1)=1
neighbour_matrix(y1,j)=1
else
goto 100
end if
end if
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(fileid1,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(fileid1,*)
end do
deallocate(up_matrix)
end subroutine sub
!degree度
subroutine node_degree()
implicit none
integer :: i,j,number
allocate(degree(N))
do i=1,N,1
number=0
do j=1,N,1
if(neighbour_matrix(i,j)==1) then
number=number+1
end if
end do
degree(i)=number
write(fileid2,*) i,number
end do
close(fileid2)
end subroutine node_degree
!distribution,度分布
subroutine distribution()
implicit none
integer :: i,j,number1,max_degree=0,min_degree=10000000
!找到最大值、最小值
do i=1,N,1
if(max_degree<degree(i)) then
max_degree=degree(i)
end if
if(min_degree>degree(i)) then
min_degree=degree(i)
end if
end do
!统计度分布
if(min_degree==max_degree) then
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
else
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
end if
close(fileid3)
end subroutine distribution
!集聚系数Clustering coefficient
subroutine Concentration()
implicit none
real :: C_average=0.0
integer :: i,j,a,number2
allocate(E(N))
allocate(C(N))
!Ci=2*E(i)/[K(i)*(K(i)-1)]
E=0
do i=1,N,1
number2=0
do j=1,N,1
if(neighbour_matrix(i,j)==1) then
do a=1,N,1
if(i/=a) then
if(neighbour_matrix(a,j)==1.and.neighbour_matrix(i,a)==1) then
number2=number2+1
end if
end if
end do
end if
end do
E(i)=number2/2 !E(i)为节点邻居的所有连边数
end do
C=0.0
do i=1,N,1
if(degree(i)-1<=0.or.degree(i)==0) then
C(i)=0.0
else
C(i)=2.0*E(i)/(degree(i)*(degree(i)-1))
end if
write(fileid4,*) i,C(i)
C_average=C_average+C(i)
end do
C_average=C_average/N !聚集系数C
write(*,*) "C=",C_average
close(fileid4)
end subroutine Concentration
!最短路径长度
subroutine shortPath(node1,node2)
implicit none
integer :: node1,node2 !两个节点
integer :: i,j,a,b
real :: sum_path=0,L
logical :: status=.true. !true表示网络连通
integer,allocatable :: P(:,:),neighbour_matrix_path(:,:),sequence(:)
allocate(neighbour_matrix_path(N,N))
allocate(P(N,N))
allocate(sequence(N))
neighbour_matrix_path=neighbour_matrix
P=0
sequence=0
!生成节点路径大小矩阵
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)==0) then
neighbour_matrix_path(i,j)=Infinity
neighbour_matrix_path(j,i)=Infinity
end if
end do
end do
if(node1<=N.and.node2<=N.and.node1/=node2) then
!广度优先遍历,使用Floyd算法
do a=1,N,1
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)>neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)) then
neighbour_matrix_path(i,j)=neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)
neighbour_matrix_path(j,i)=neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)
P(i,j)=a
end if
end do
end do
end do
!输出节点路径大小矩阵,及最短路径矩阵
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') neighbour_matrix_path(i,j)
end do
write(fileid5,*)
end do
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') P(i,j)
end do
write(fileid5,*)
end do
if(neighbour_matrix_path(node1,node2)==Infinity) then
write(*,*) node1,node2,"不存在路径"
else
write(*,*) "节点",node1,"和节点",node2,"的最短路径为:",neighbour_matrix_path(node1,node2)
end if
else
write(*,*) "输入节点错误!"
end if
close(fileid5)
!平均路径长度,L=1/(N*(N-1))*累加(d(i,j))
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)/=Infinity) then
sum_path=sum_path+neighbour_matrix_path(i,j)
else
status=.false.
end if
end do
end do
L=sum_path/(N*(N-1)/2)
write(*,*) "平均路径长度L=",L
if(status.eqv..true.) then
write(*,*) "网络连通!"
else
write(*,*) "网络不连通!"
end if
deallocate(neighbour_matrix_path)
deallocate(P)
deallocate(sequence)
end subroutine shortPath
end module neighbour
program main
use neighbour
implicit none
integer :: K !N节点数量,K邻居数
integer :: node1,node2 !两个节点
open(fileid1,file='matrix.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "请输入单节点邻居总数:"
read(*,*) K
call sub(N,K)
write(*,*) "均匀随机网络生成完毕!"
open(fileid2,file='degree.txt')
call node_degree()
write(*,*) "节点__度 数据生成完毕"
open(fileid3,file='distribution.txt')
call distribution()
write(*,*) "度__数量 数据生成完毕"
open(fileid4,file='Concentration.txt')
write(*,*) "集聚系数:"
call Concentration()
open(fileid5,file='shortPath.txt')
write(*,*) "请输入两个节点(不大于",N,")"
read(*,*) node1,node2
call shortPath(node1,node2)
deallocate(neighbour_matrix)
deallocate(degree)
deallocate(E)
deallocate(C)
stop
end program main

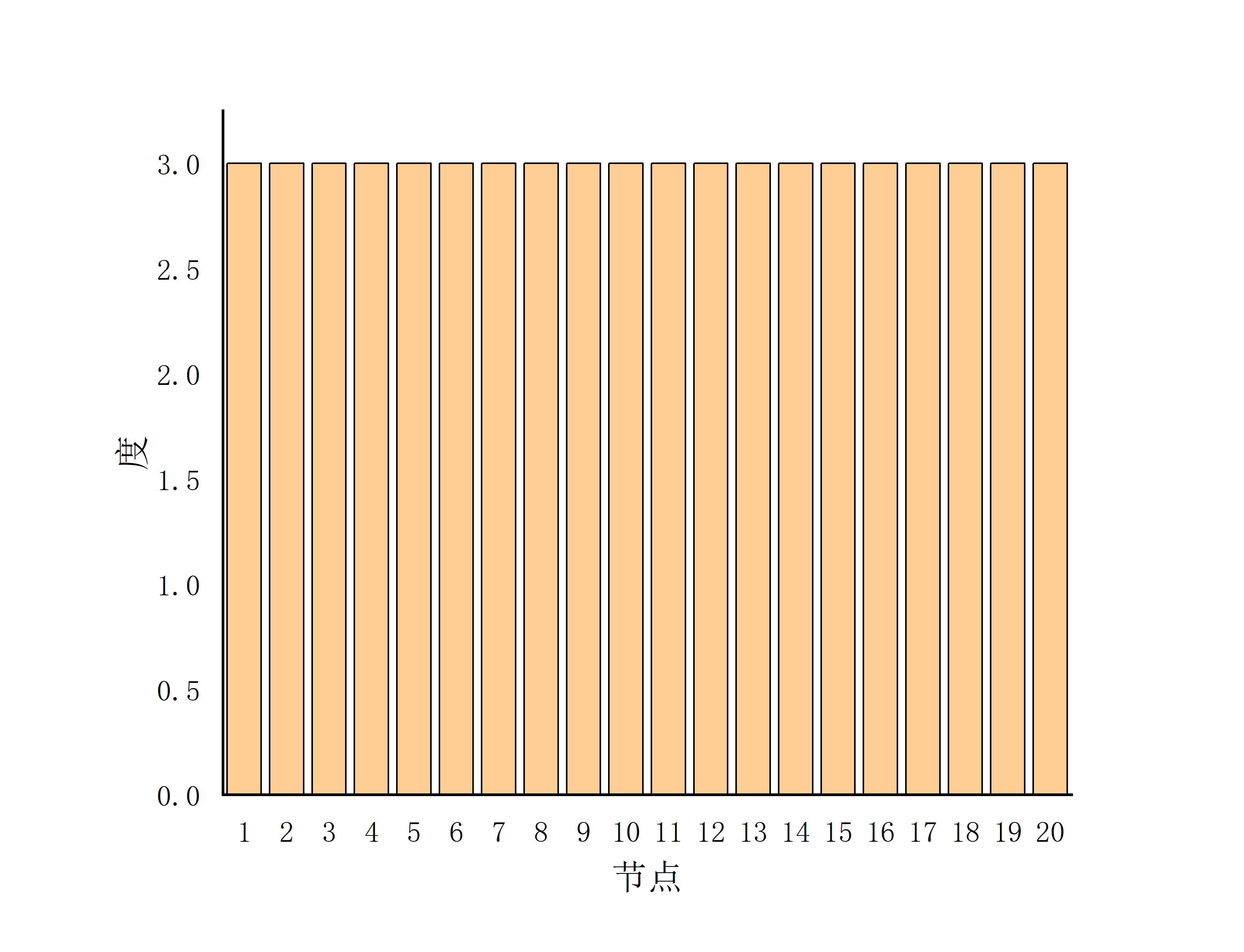





小世界模型
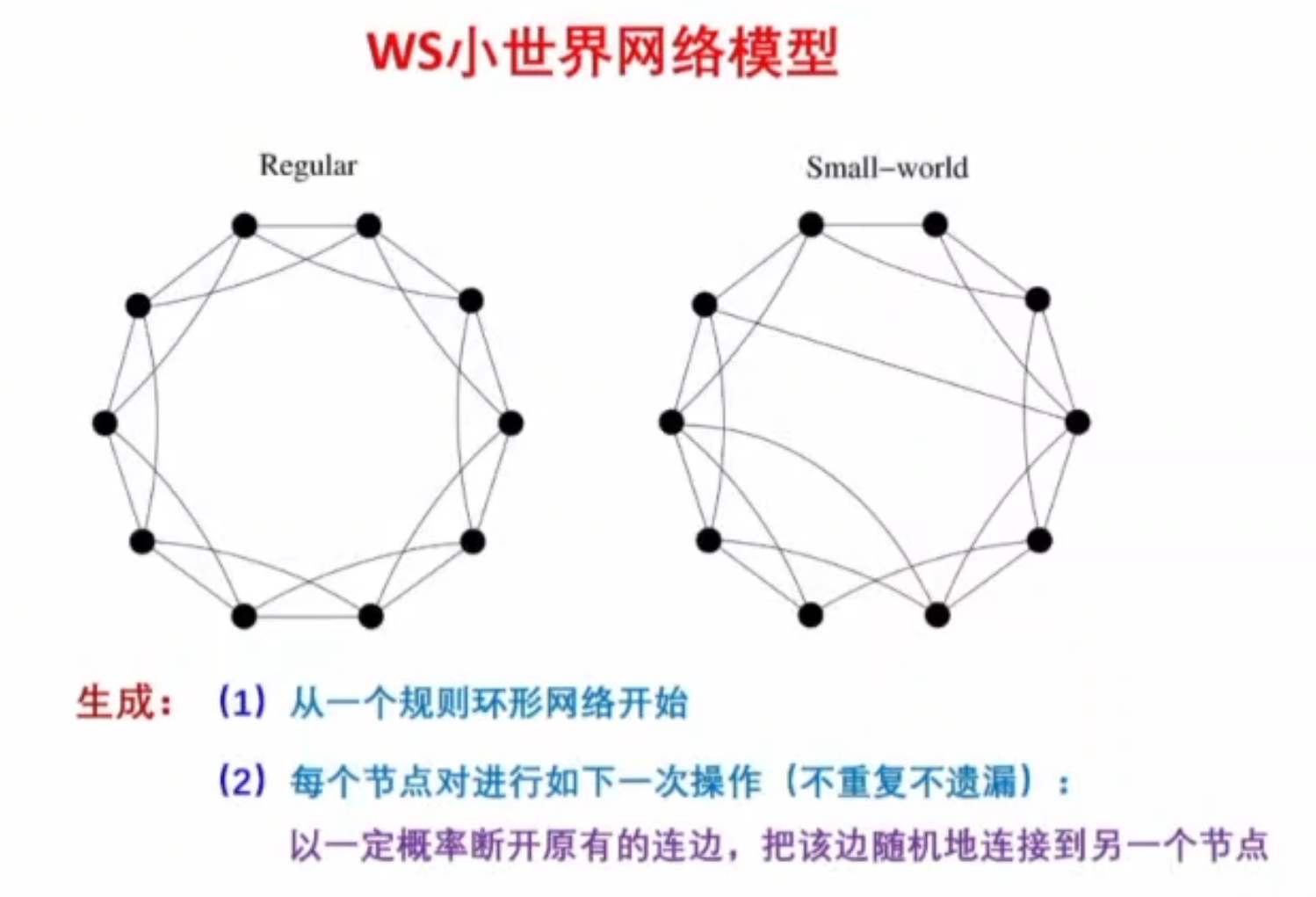
WS
- 由
Watts和Strogatz提出,在生成网络过程中保证网络连通性需要很大的算法代价。 - 断边重连,节点和边都不变
module neighbour
implicit none
integer,parameter :: fileid1=10,fileid2=20,fileid3=30,fileid4=40,fileid5=50,Infinity=10000!Infinity代替无穷大
integer,allocatable :: neighbour_matrix(:,:),degree(:),E(:)
real,allocatable :: C(:)
integer :: N,K
real :: C_average=0.0,L
common N,K,C_average,L
contains
subroutine sub(N,K,P_break)
implicit none
integer :: N,K !单节点K个邻居
integer :: i,j,y
real :: x,p_half,P,P_break
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
!赋值节点关系
!分析可知:邻边矩阵对应|i-j|>=N-K/2或者|i-j|<=K/2
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
!断边重连
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
call random_number(P)
if(P<P_break) then
100 call random_number(p_half) !判断选择边的左节点与另一个节点相连,还是右节点
call random_number(x) !随机选择另一个节点nint(x*N+1)-1
y=nint((x-0.51/N)*N+1)!取N的概率比其它少0.02
if(p_half<0.5) then !左节点连另一个节点
if(neighbour_matrix(i,y)==0.and.i/=y) then
neighbour_matrix(i,j)=0
neighbour_matrix(j,i)=0
neighbour_matrix(i,y)=1
neighbour_matrix(y,i)=1
else
goto 100
end if
else !右节点连另一个节点
if(neighbour_matrix(j,y)==0&
.and.j/=y) then
neighbour_matrix(i,j)=0
neighbour_matrix(j,i)=0
neighbour_matrix(j,y)=1
neighbour_matrix(y,j)=1
else
goto 100
end if
end if
end if
end if
end do
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(fileid1,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(fileid1,*)
end do
close(fileid1)
end subroutine sub
!degree度
subroutine node_degree()
implicit none
integer :: i,j,number
allocate(degree(N))
do i=1,N,1
number=0
do j=1,N,1
if(neighbour_matrix(i,j)==1) then
number=number+1
end if
end do
degree(i)=number
write(fileid2,*) i,number
end do
close(fileid2)
end subroutine node_degree
!distribution,度分布
subroutine distribution()
implicit none
integer :: i,j,number1,max_degree=0,min_degree=10000000
!找到最大值、最小值
do i=1,N,1
if(max_degree<degree(i)) then
max_degree=degree(i)
end if
if(min_degree>degree(i)) then
min_degree=degree(i)
end if
end do
!统计度分布
if(min_degree==max_degree) then
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
else
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
end if
close(fileid3)
end subroutine distribution
!集聚系数Clustering coefficient
subroutine Concentration()
implicit none
integer :: i,j,a,number2
real :: C_sum=0.0
allocate(E(N))
allocate(C(N))
!Ci=2*E(i)/[K(i)*(K(i)-1)]
E=0
do i=1,N,1
number2=0
do j=1,N,1
if(neighbour_matrix(i,j)==1) then
do a=1,N,1
if(i/=a) then
if(neighbour_matrix(a,j)==1.and.neighbour_matrix(i,a)==1) then
number2=number2+1
end if
end if
end do
end if
end do
E(i)=number2/2 !E(i)为节点邻居的所有连边数
end do
C=0.0
do i=1,N,1
if(degree(i)-1<=0.or.degree(i)==0) then
C(i)=0.0
else
C(i)=2.0*E(i)/(degree(i)*(degree(i)-1))
end if
write(fileid4,*) i,C(i)
C_sum=C_sum+C(i)
end do
C_average=C_sum/N !聚集系数C
C_sum=0.0
write(*,*) "C=",C_average
close(fileid4)
end subroutine Concentration
!最短路径长度
subroutine shortPath(node1,node2)
implicit none
integer :: node1,node2 !两个节点
integer :: i,j,a,b
real :: sum_path
logical :: status=.true. !true表示网络连通
integer,allocatable :: P(:,:),neighbour_matrix_path(:,:),sequence(:)
allocate(neighbour_matrix_path(N,N))
allocate(P(N,N))
allocate(sequence(N))
neighbour_matrix_path=neighbour_matrix
P=0
sequence=0
!生成节点路径大小矩阵
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)==0) then
neighbour_matrix_path(i,j)=Infinity
neighbour_matrix_path(j,i)=Infinity
end if
end do
end do
if(node1<=N.and.node2<=N.and.node1/=node2) then
!广度优先遍历,使用Floyd算法
do a=1,N,1
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)>neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)) then
neighbour_matrix_path(i,j)=neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)
neighbour_matrix_path(j,i)=neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)
P(i,j)=a
end if
end do
end do
end do
!输出节点路径大小矩阵,及最短路径矩阵
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') neighbour_matrix_path(i,j)
end do
write(fileid5,*)
end do
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') P(i,j)
end do
write(fileid5,*)
end do
if(neighbour_matrix_path(node1,node2)==Infinity) then
write(*,*) node1,node2,"不存在路径"
else
write(*,*) "节点",node1,"和节点",node2,"的最短路径为:",neighbour_matrix_path(node1,node2) !这里因为权重为1,所以处理了上三角矩阵,便于查看原矩阵情况
end if
else
write(*,*) "输入节点错误!"
end if
close(fileid5)
!平均路径长度,L=1/(N*(N-1))*累加(d(i,j))
sum_path=0.0
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)/=Infinity) then
sum_path=sum_path+neighbour_matrix_path(i,j)
else
status=.false.
end if
end do
end do
L=sum_path/(N*(N-1)/2)
write(*,*) "平均路径长度L=",L
if(status.eqv..true.) then
write(*,*) "网络连通!"
else
write(*,*) "网络不连通!"
end if
deallocate(neighbour_matrix_path)
deallocate(P)
deallocate(sequence)
end subroutine shortPath
end module neighbour
program main
use neighbour
implicit none
real :: i=0.0,j=0.0,C_0,C_P,L_0,L_P
integer :: node1,node2 !两个节点
real :: P_break
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "请输入单节点邻居总数:"
read(*,*) K
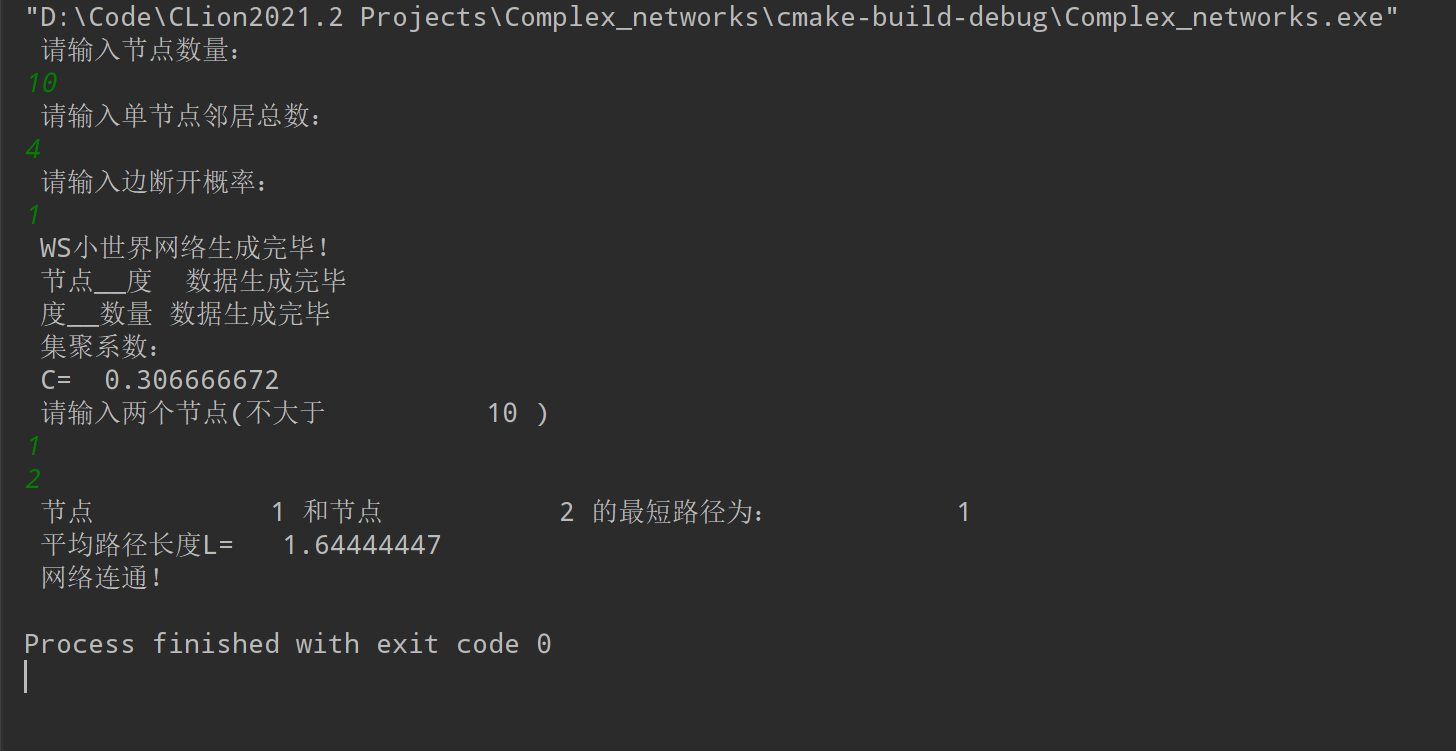
write(*,*) "请输入边断开概率:"
read(*,*) P_break
call random_seed()
open(fileid1,file='matrix.txt')
call sub(N,K,P_break)
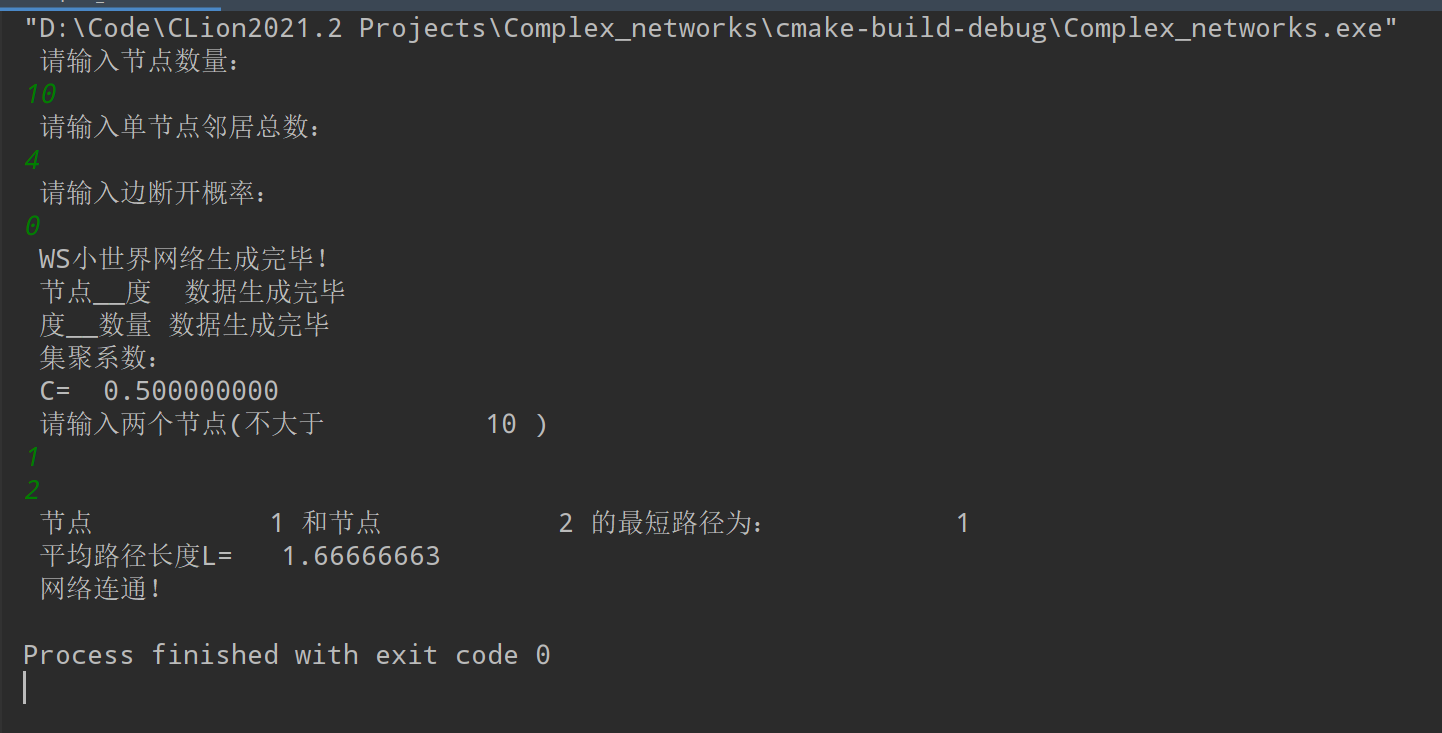
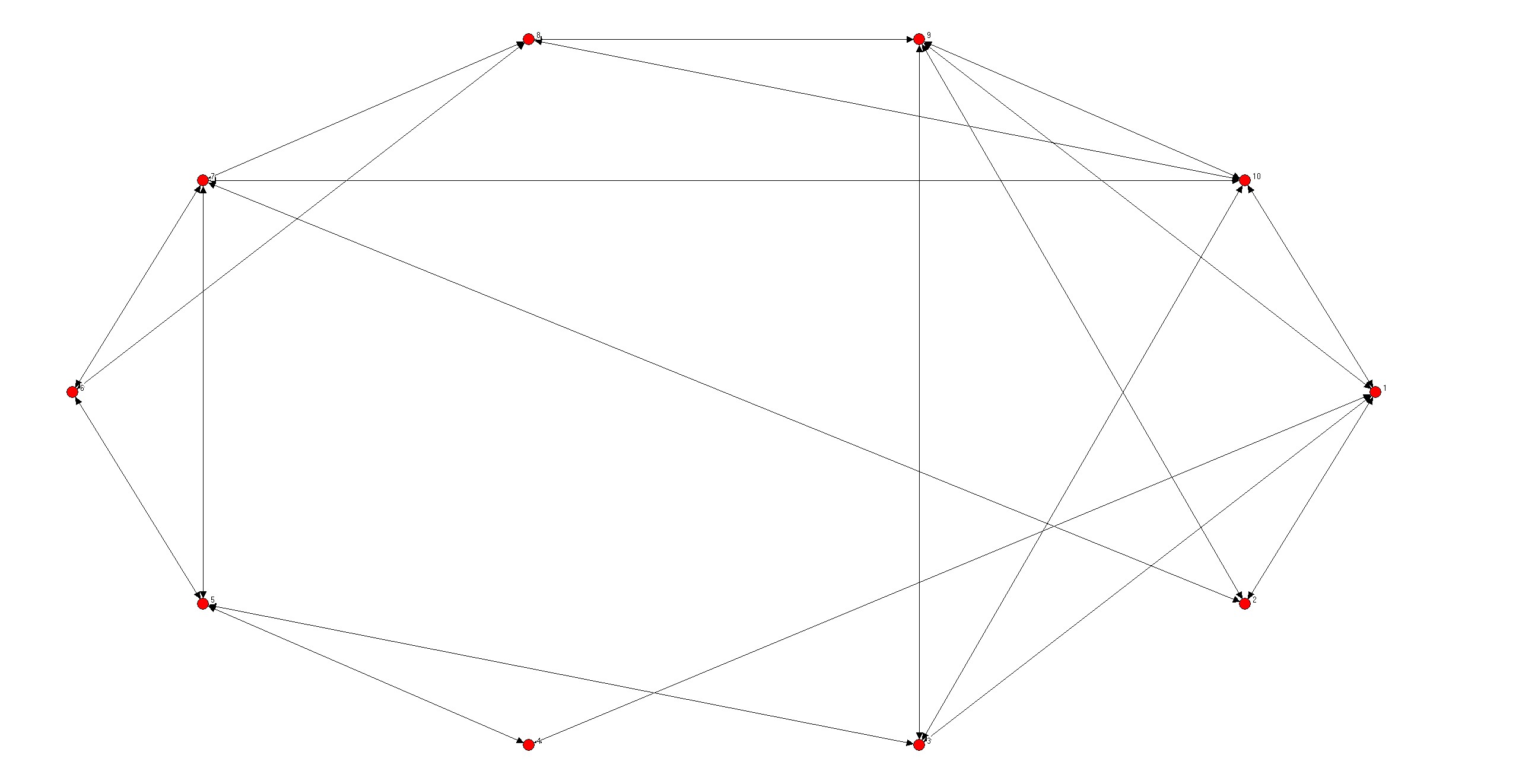
write(*,*) "WS小世界网络生成完毕!"
open(fileid2,file='degree.txt')
call node_degree()
write(*,*) "节点__度 数据生成完毕"
open(fileid3,file='distribution.txt')
call distribution()
write(*,*) "度__数量 数据生成完毕"
open(fileid4,file='Concentration.txt')
write(*,*) "集聚系数:"
call Concentration()
open(fileid5,file='shortPath.txt')
write(*,*) "请输入两个节点(不大于",N,")"
read(*,*) node1,node2
call shortPath(node1,node2)
deallocate(neighbour_matrix)
deallocate(degree)
deallocate(E)
deallocate(C)
stop
end program main




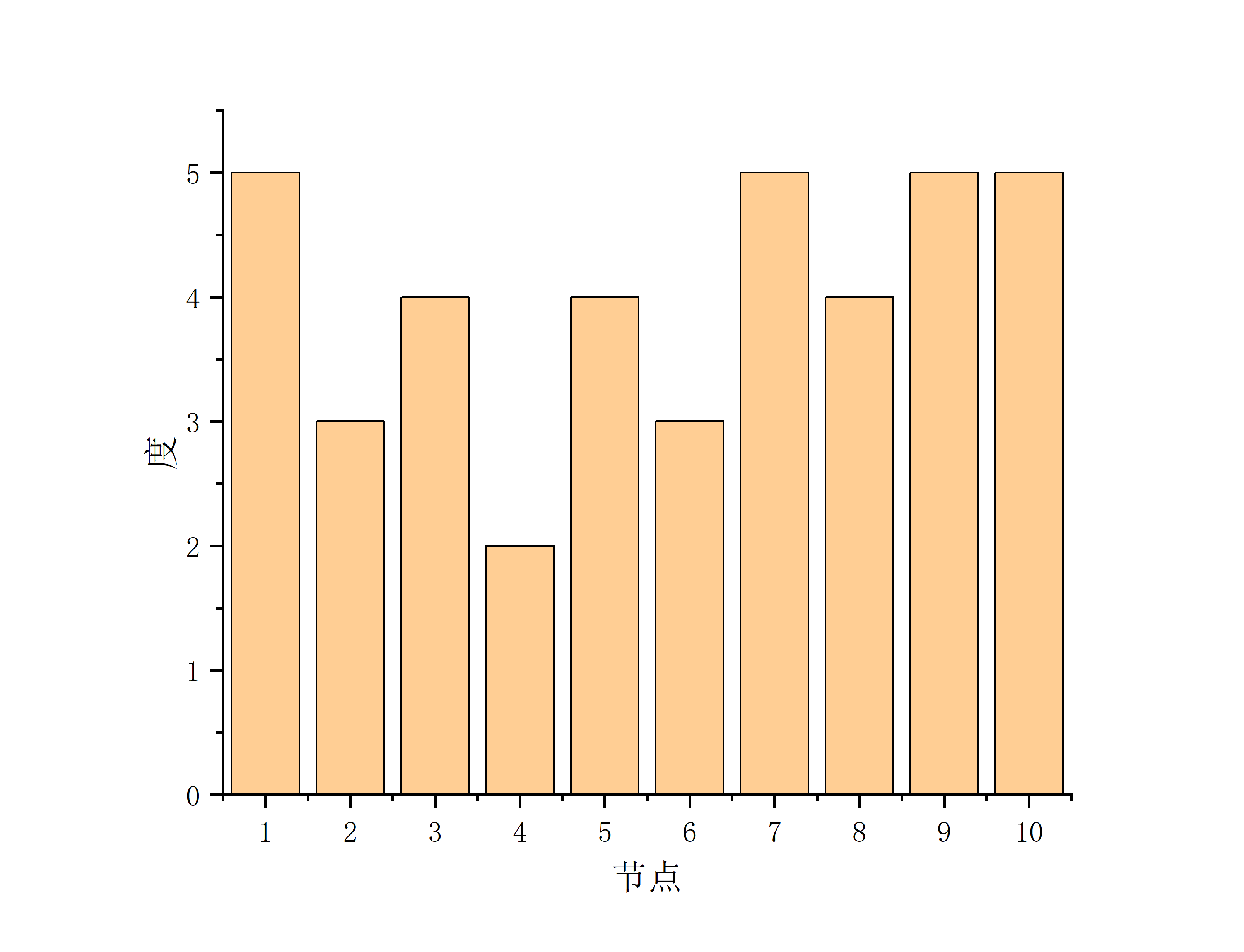









NW
- 由
Newman和Watts提出的,非常容易保证网络的连通性,大多数具有小世界性质的网络通过NW来构建。 - 加边重连,节点不变

module neighbour
implicit none
integer,parameter :: fileid1=10,fileid2=20,fileid3=30,fileid4=40,fileid5=50,Infinity=10000!Infinity代替无穷大
integer,allocatable :: neighbour_matrix(:,:),degree(:),E(:)
real,allocatable :: C(:)
integer :: N
common N
contains
subroutine sub(N,K,P_con)
implicit none
integer :: N,K !单节点K个邻居
integer :: i,j,a,b,number
real :: x,P,P_con
integer :: y
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
!赋值节点关系
!分析可知:邻边矩阵对应|i-j|>=N-K/2或者|i-j|<=K/2
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
!均匀随机化
call random_seed()
do i=1,N,1
call random_number(P)
if(P<=P_con) then
100 call random_number(x)
y=nint((x-0.51/N)*N+1)!取N的概率比其它少0.02
number=0
do a=1,N,1
if(neighbour_matrix(i,a)==1) then
number=number+1
end if
end do
if(number<N-1) then !判断该节点是否可以加边,可以就加,不行就遍历下一个节点
if(neighbour_matrix(i,y)==0.and.i/=y) then
neighbour_matrix(i,y)=1
neighbour_matrix(y,i)=1
else
goto 100
end if
else
cycle
end if
end if
end do
!输出矩阵
do i=1,N,1
do j=1,N,1
write(fileid1,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(fileid1,*)
end do
end subroutine sub
!degree度
subroutine node_degree()
implicit none
integer :: i,j,number
allocate(degree(N))
do i=1,N,1
number=0
do j=1,N,1
if(neighbour_matrix(i,j)==1) then
number=number+1
end if
end do
degree(i)=number
write(fileid2,*) i,number
end do
close(fileid2)
end subroutine node_degree
!distribution,度分布
subroutine distribution()
implicit none
integer :: i,j,number1,max_degree=0,min_degree=10000000
!找到最大值、最小值
do i=1,N,1
if(max_degree<degree(i)) then
max_degree=degree(i)
end if
if(min_degree>degree(i)) then
min_degree=degree(i)
end if
end do
!统计度分布
if(min_degree==max_degree) then
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
else
do i=min_degree,max_degree,1
number1=0
do j=1,N,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
end if
close(fileid3)
end subroutine distribution
!集聚系数Clustering coefficient
subroutine Concentration()
implicit none
real :: C_average=0.0
integer :: i,j,a,number2
allocate(E(N))
allocate(C(N))
!Ci=2*E(i)/[K(i)*(K(i)-1)]
E=0
do i=1,N,1
number2=0
do j=1,N,1
if(neighbour_matrix(i,j)==1) then
do a=1,N,1
if(i/=a) then
if(neighbour_matrix(a,j)==1.and.neighbour_matrix(i,a)==1) then
number2=number2+1
end if
end if
end do
end if
end do
E(i)=number2/2 !E(i)为节点邻居的所有连边数
end do
C=0.0
do i=1,N,1
if(degree(i)-1<=0.or.degree(i)==0) then
C(i)=0.0
else
C(i)=2.0*E(i)/(degree(i)*(degree(i)-1))
end if
write(fileid4,*) i,C(i)
C_average=C_average+C(i)
end do
C_average=C_average/N !聚集系数C
write(*,*) "C=",C_average
close(fileid4)
end subroutine Concentration
!最短路径长度
subroutine shortPath(node1,node2)
implicit none
integer :: node1,node2 !两个节点
integer :: i,j,a,b
real :: sum_path=0,L
logical :: status=.true. !true表示网络连通
integer,allocatable :: P(:,:),neighbour_matrix_path(:,:),sequence(:)
allocate(neighbour_matrix_path(N,N))
allocate(P(N,N))
allocate(sequence(N))
neighbour_matrix_path=neighbour_matrix
P=0
sequence=0
!生成节点路径大小矩阵
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)==0) then
neighbour_matrix_path(i,j)=Infinity
neighbour_matrix_path(j,i)=Infinity
end if
end do
end do
if(node1<=N.and.node2<=N.and.node1/=node2) then
!广度优先遍历,使用Floyd算法
do a=1,N,1
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)>neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)) then
neighbour_matrix_path(i,j)=neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)
neighbour_matrix_path(j,i)=neighbour_matrix_path(i,a)+neighbour_matrix_path(a,j)
P(i,j)=a
end if
end do
end do
end do
!输出节点路径大小矩阵,及最短路径矩阵
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') neighbour_matrix_path(i,j)
end do
write(fileid5,*)
end do
do i=1,N,1
do j=1,N,1
write(fileid5,"(I10)",advance='no') P(i,j)
end do
write(fileid5,*)
end do
if(neighbour_matrix_path(node1,node2)==Infinity) then
write(*,*) node1,node2,"不存在路径"
else
write(*,*) "节点",node1,"和节点",node2,"的最短路径为:",neighbour_matrix_path(node1,node2) !这里因为权重为1,所以处理了上三角矩阵,便于查看原矩阵情况
end if
else
write(*,*) "输入节点错误!"
end if
close(fileid5)
!平均路径长度,L=1/(N*(N-1))*累加(d(i,j))
do i=1,N-1,1
do j=i+1,N,1
if(neighbour_matrix_path(i,j)/=Infinity) then
sum_path=sum_path+neighbour_matrix_path(i,j)
else
status=.false.
end if
end do
end do
L=sum_path/(N*(N-1)/2)
write(*,*) "平均路径长度L=",L
if(status.eqv..true.) then
write(*,*) "网络连通!"
else
write(*,*) "网络不连通!"
end if
deallocate(neighbour_matrix_path)
deallocate(P)
deallocate(sequence)
end subroutine shortPath
end module neighbour
program main
use neighbour
implicit none
integer :: K !N节点数量,K邻居数
real :: P_con
integer :: node1,node2 !两个节点
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "请输入单节点邻居总数:"
read(*,*) K
write(*,*) "请输入节点加边概率:"
read(*,*) P_con
call random_seed()
open(fileid1,file='matrix.txt')
call sub(N,K,P_con)
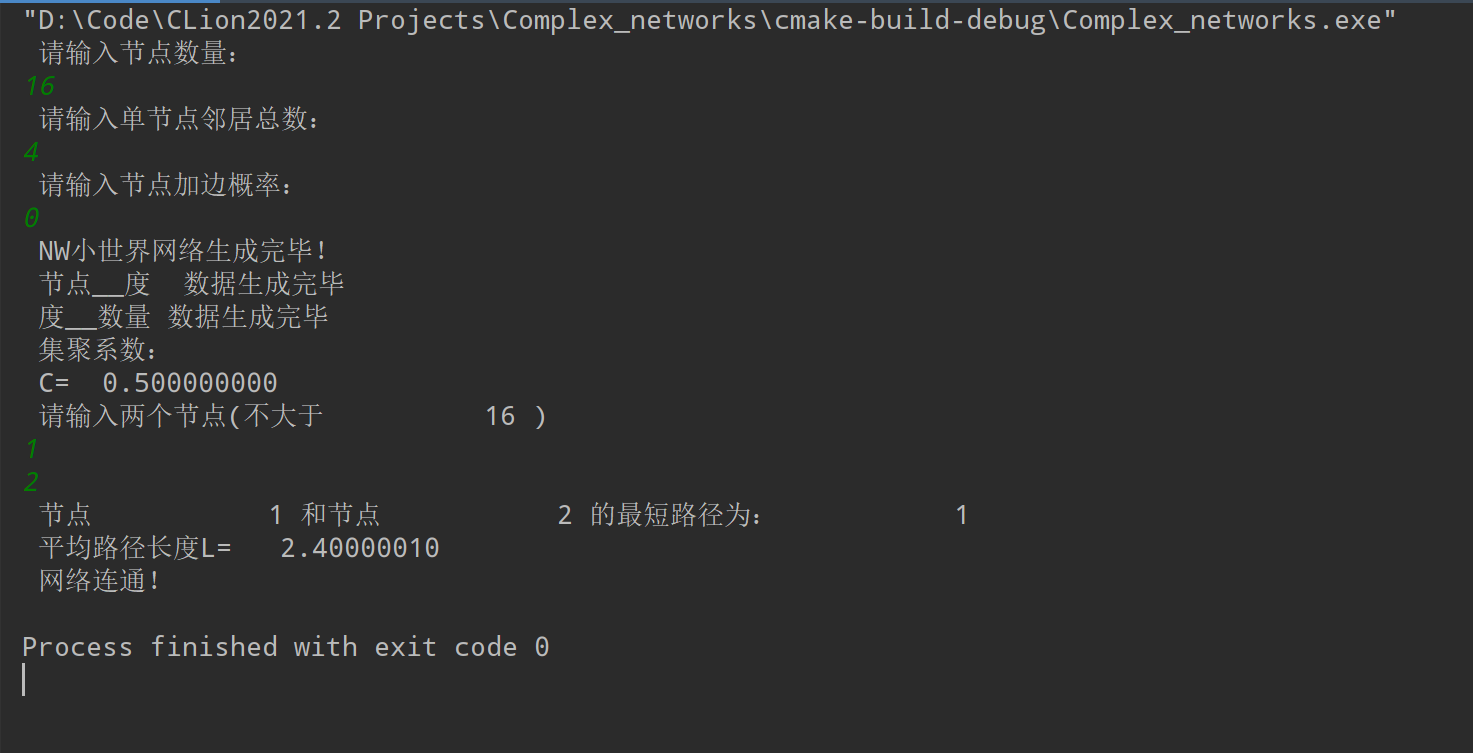
write(*,*) "NW小世界网络生成完毕!"
open(fileid2,file='degree.txt')
call node_degree()
write(*,*) "节点__度 数据生成完毕"
open(fileid3,file='distribution.txt')
call distribution()
write(*,*) "度__数量 数据生成完毕"
open(fileid4,file='Concentration.txt')
write(*,*) "集聚系数:"
call Concentration()
open(fileid5,file='shortPath.txt')
write(*,*) "请输入两个节点(不大于",N,")"
read(*,*) node1,node2
call shortPath(node1,node2)
deallocate(neighbour_matrix)
deallocate(degree)
deallocate(E)
deallocate(C)
stop
end program main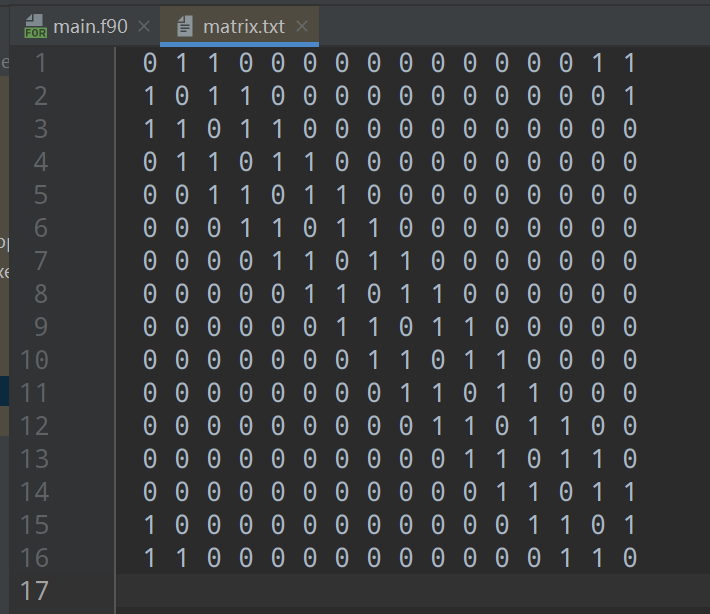
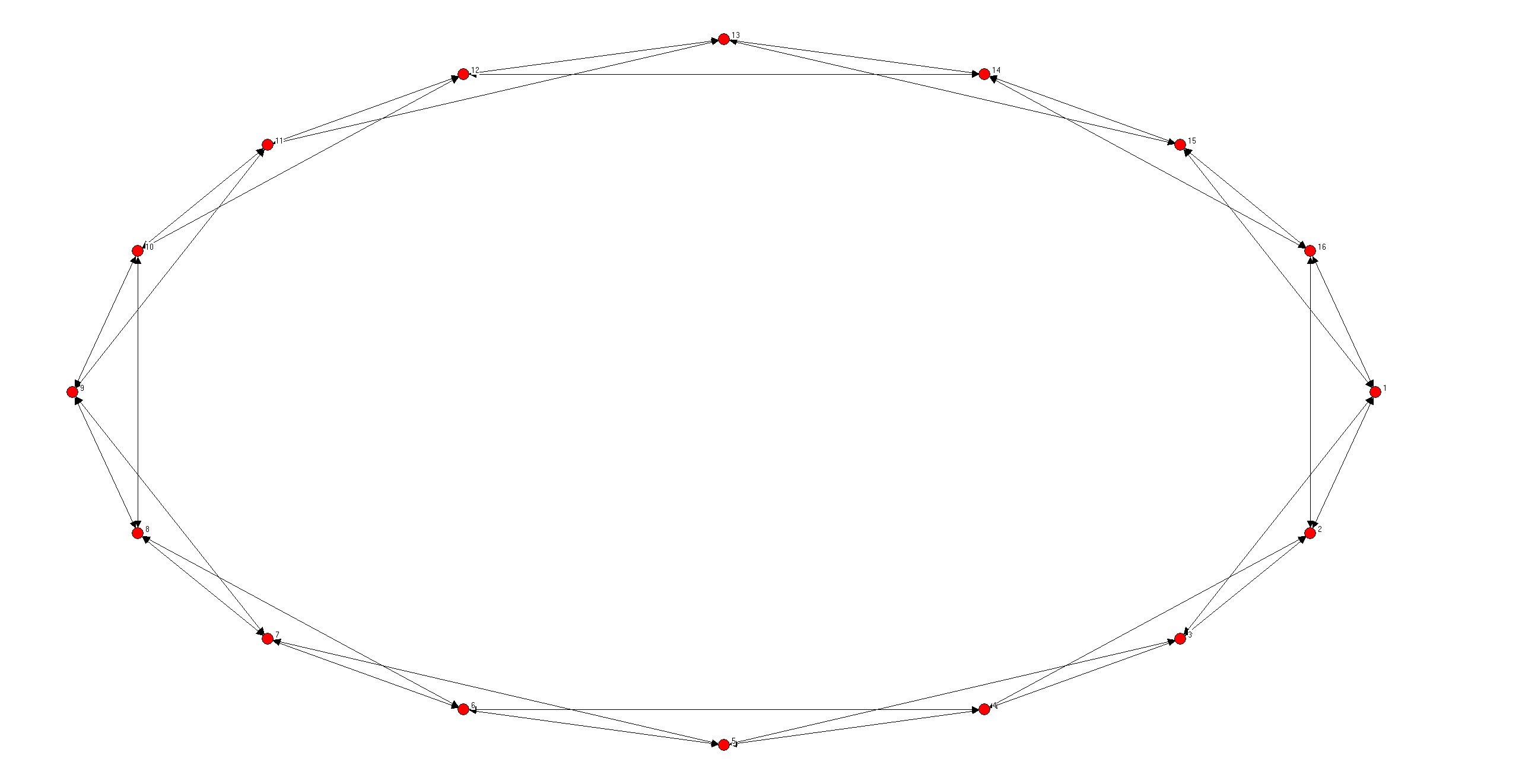





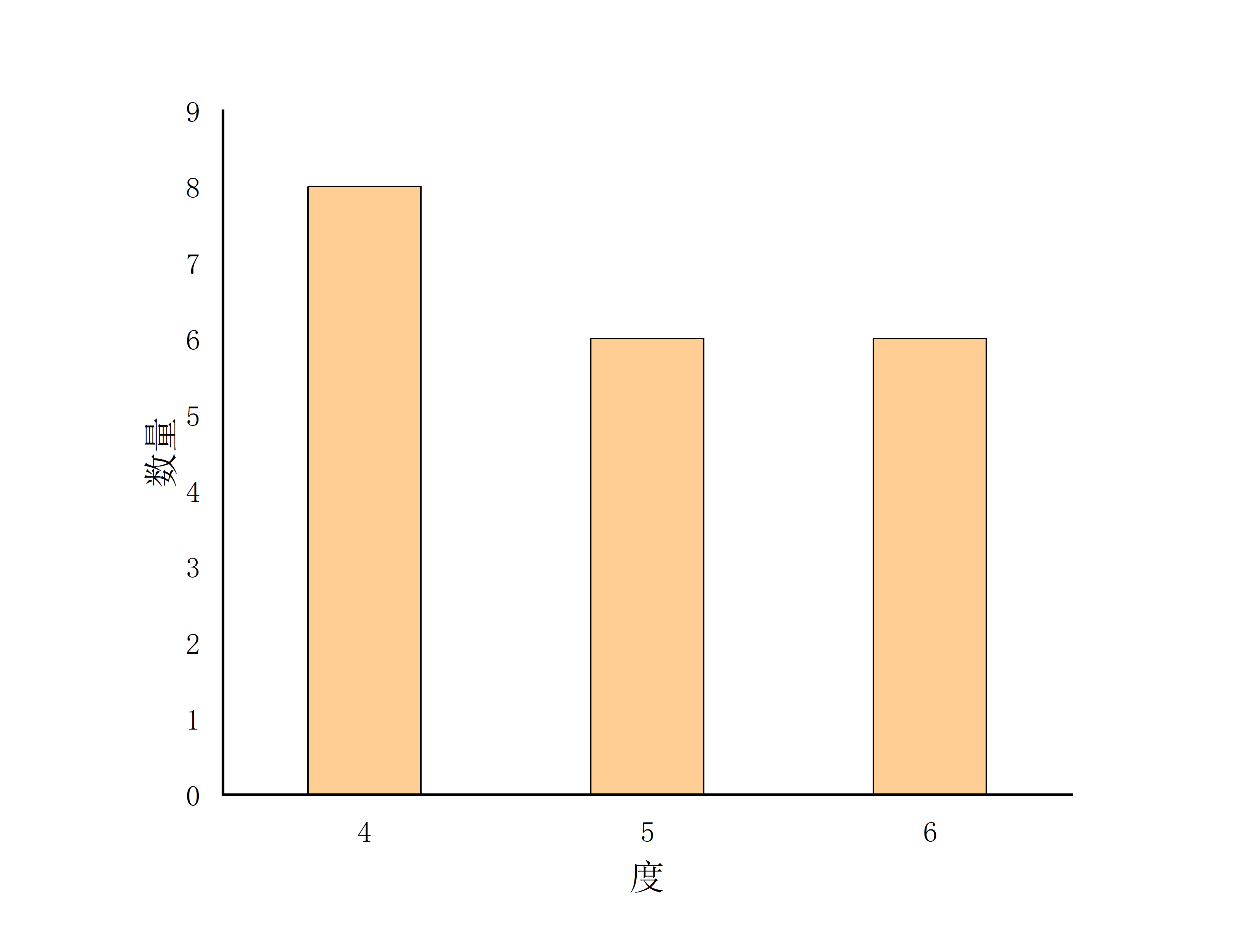


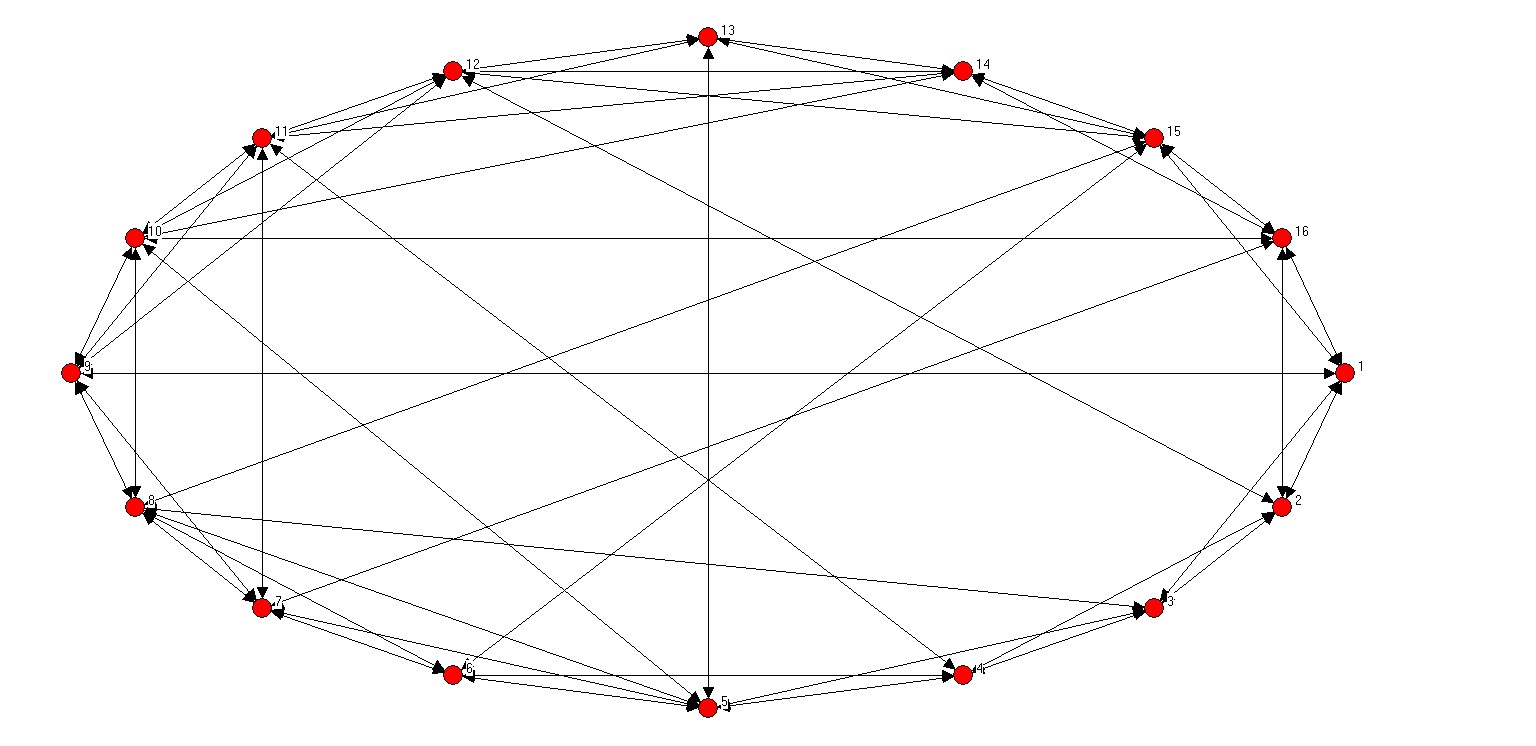

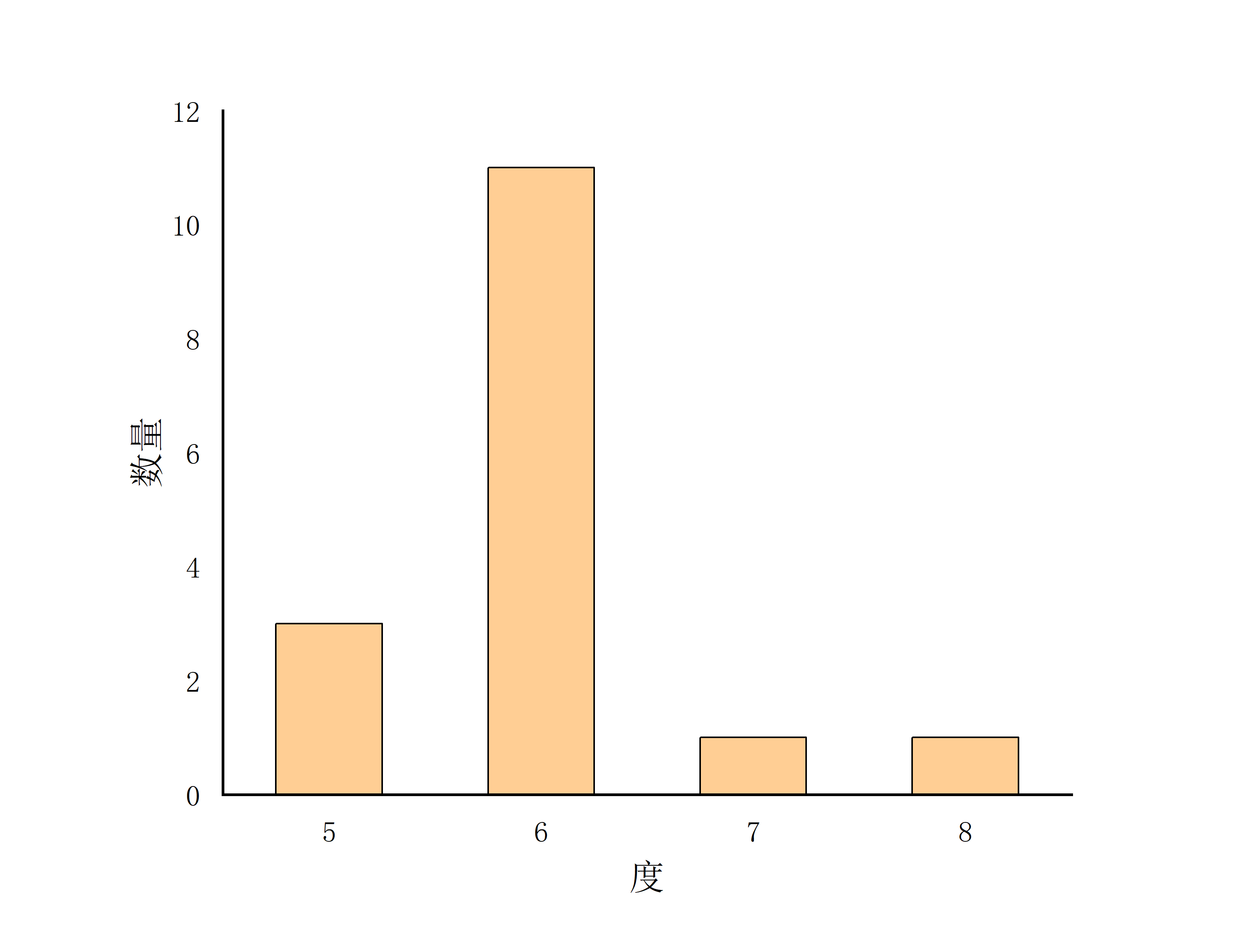
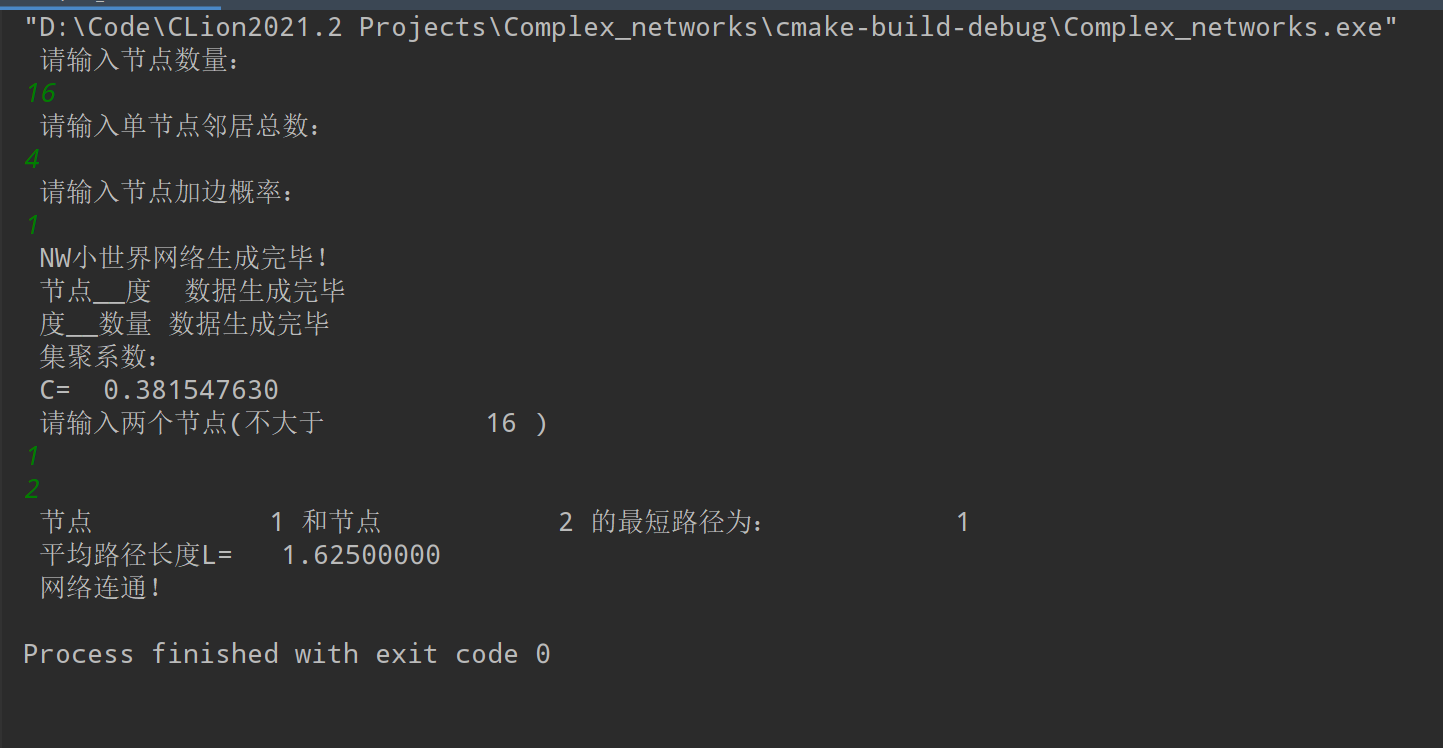
无标度网络
BA
- 由
Barabasi和Albert提出的标准模型,生成的网络的度分布是幂律指数为3的幂律形式。
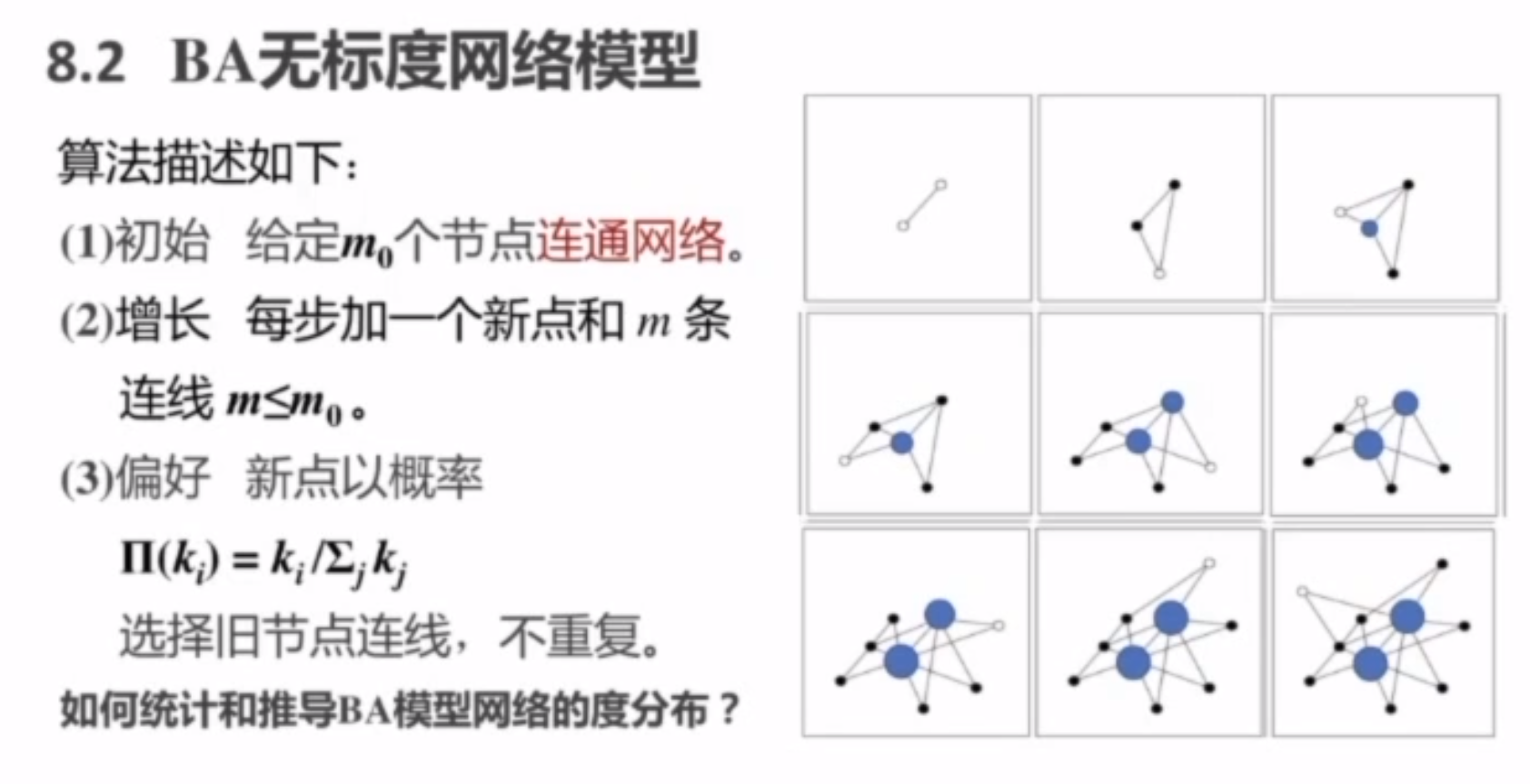
module noStandard
implicit none
integer,parameter :: fileid1=10,fileid2=20,fileid3=30,fileid4=40,fileid5=50,Infinity=10000!Infinity代替无穷大
integer,allocatable :: er_matrix(:,:),degree(:),E(:)
real,allocatable :: C(:)
integer :: N,M
common N,M
contains
subroutine sub(N,P_ER,M,K)
implicit none
integer :: N,K,M !K新节点度
integer :: i,j,a,b
real :: sum1,sum2,sum3
real,allocatable :: sequence_1(:)
real :: x,P_ER,P
allocate(er_matrix(N+M,N+M))
allocate(sequence_1(N+M-1))
!初始化网络矩阵
er_matrix=0
!赋值节点关系
!建立ER随机网络
do i=N,2,-1
do j=i-1,1,-1
!产生随机数
call random_number(x)
if(x<P_ER) then
er_matrix(i,j)=1
er_matrix(j,i)=1
end if
end do
end do
!依次加节点,连边
do i=1,M,1
!添加节点
er_matrix(:,N+i)=0
er_matrix(N+i,:)=0
!连边
!sum1旧节点总度数
sum1=0.0
sum1=sum(er_matrix(:,:))
!sum2旧节点每个节点度数,sequence旧节点的比例情况
sequence_1=0.0
do a=1,N+i-1,1
sum2=0.0
do b=1,N+i-1,1
if(er_matrix(a,b)==1) then
sum2=sum2+1
end if
end do
sequence_1(a)=sum2/sum1
end do
do j=1,K,1
100 call random_number(P) !与旧节点连接概率
!每个节点度比例
sum3=0.0 !判断随机数P所在位置
do a=1,N+M-1,1
sum3=sum3+sequence_1(a)
if(P<=sum3) then
if(er_matrix(a,N+i)==0) then
er_matrix(a,N+i)=1
er_matrix(N+i,a)=1
exit
else
goto 100
end if
end if
end do
end do
end do
!输出矩阵
do i=1,N+M,1
do j=1,N+M,1
write(fileid1,"(I2)",advance='no') er_matrix(i,j)
end do
write(fileid1,*)
end do
close(fileid1)
deallocate(sequence_1)
end subroutine sub
!degree度
subroutine node_degree()
implicit none
integer :: i,j,number
allocate(degree(N+M))
do i=1,N+M,1
number=0
do j=1,N+M,1
if(er_matrix(i,j)==1) then
number=number+1
end if
end do
degree(i)=number
write(fileid2,*) i,number
end do
close(fileid2)
end subroutine node_degree
!distribution,度分布
subroutine distribution()
implicit none
integer :: i,j,number1,max_degree=0,min_degree=10000000
!找到最大值、最小值
do i=1,N+M,1
if(max_degree<degree(i)) then
max_degree=degree(i)
end if
if(min_degree>degree(i)) then
min_degree=degree(i)
end if
end do
!统计度分布
if(min_degree==max_degree) then
do i=min_degree,max_degree,1
number1=0
do j=1,N+M,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
else
do i=min_degree,max_degree,1
number1=0
do j=1,N+M,1
if(degree(j)==i) then
number1=number1+1
end if
end do
write(fileid3,*) i,number1
end do
end if
close(fileid3)
end subroutine distribution
!集聚系数Clustering coefficient
subroutine Concentration()
implicit none
real :: C_average=0.0
integer :: i,j,a,number2
allocate(E(N+M))
allocate(C(N+M))
!Ci=2*E(i)/[K(i)*(K(i)-1)]
E=0
do i=1,N+M,1
number2=0
do j=1,N+M,1
if(er_matrix(i,j)==1) then
do a=1,N+M,1
if(i/=a) then
if(er_matrix(a,j)==1.and.er_matrix(i,a)==1) then
number2=number2+1
end if
end if
end do
end if
end do
E(i)=number2/2 !E(i)为节点邻居的所有连边数
end do
C=0.0
do i=1,N+M,1
if(degree(i)-1<=0.or.degree(i)==0) then
C(i)=0.0
else
C(i)=2.0*E(i)/(degree(i)*(degree(i)-1))
end if
write(fileid4,*) i,C(i)
C_average=C_average+C(i)
end do
C_average=C_average/N !聚集系数C
write(*,*) "C=",C_average
close(fileid4)
end subroutine Concentration
!最短路径长度
subroutine shortPath(node1,node2)
implicit none
integer :: node1,node2 !两个节点
integer :: i,j,a,b
real :: sum_path=0,L
logical :: status=.true. !true表示网络连通
integer,allocatable :: P(:,:),er_matrix_path(:,:),sequence(:)
allocate(er_matrix_path(N+M,N+M))
allocate(P(N+M,N+M))
allocate(sequence(N+M))
er_matrix_path=er_matrix
P=0
sequence=0
!生成节点路径大小矩阵
do i=1,N+M-1,1
do j=i+1,N+M,1
if(er_matrix_path(i,j)==0) then
er_matrix_path(i,j)=Infinity
er_matrix_path(j,i)=Infinity
end if
end do
end do
if(node1<=N+M.and.node2<=N+M.and.node1/=node2) then
!广度优先遍历,使用Floyd算法
do a=1,N+M,1
do i=1,N+M-1,1
do j=i+1,N+M,1
if(er_matrix_path(i,j)>er_matrix_path(i,a)+er_matrix_path(a,j)) then
er_matrix_path(i,j)=er_matrix_path(i,a)+er_matrix_path(a,j)
er_matrix_path(j,i)=er_matrix_path(i,a)+er_matrix_path(a,j)
P(i,j)=a
end if
end do
end do
end do
!输出节点路径大小矩阵,及最短路径矩阵
do i=1,N+M,1
do j=1,N+M,1
write(fileid5,"(I10)",advance='no') er_matrix_path(i,j)
end do
write(fileid5,*)
end do
do i=1,N+M,1
do j=1,N+M,1
write(fileid5,"(I10)",advance='no') P(i,j)
end do
write(fileid5,*)
end do
if(er_matrix_path(node1,node2)==Infinity) then
write(*,*) node1,node2,"不存在路径"
else
write(*,*) "节点",node1,"和节点",node2,"的最短路径为:",er_matrix_path(node1,node2)
end if
else
write(*,*) "输入节点错误!"
end if
close(fileid5)
!平均路径长度,L=1/(N*(N-1))*累加(d(i,j))
do i=1,N+M-1,1
do j=i+1,N+M,1
if(er_matrix_path(i,j)/=Infinity) then
sum_path=sum_path+er_matrix_path(i,j)
else
status=.false.
end if
end do
end do
L=sum_path/((N+M)*(N+M-1)/2)
write(*,*) "平均路径长度L=",L
if(status.eqv..true.) then
write(*,*) "网络连通!"
else
write(*,*) "网络不连通!"
end if
deallocate(er_matrix_path)
deallocate(P)
deallocate(sequence)
end subroutine shortPath
end module noStandard
program main
use noStandard
implicit none
integer :: K !K新节点度
real :: P_ER !随机网络生成概率
integer :: node1,node2 !两个节点
open(fileid1,file='matrix.txt')
write(*,*) "请输入节点数量:"
read(*,*) N
write(*,*) "生成ER随机网络概率:"
read(*,*) P_ER
write(*,*) "请输入添加节点总数:"
read(*,*) M
write(*,*) "请输入新节点的度:"
read(*,*) K
call random_seed()
call sub(N,P_ER,M,K)
write(*,*) "BA无标度网络生成完毕!"
open(fileid2,file='degree.txt')
call node_degree()
write(*,*) "节点__度 数据生成完毕"
open(fileid3,file='distribution.txt')
call distribution()
write(*,*) "度__数量 数据生成完毕"
open(fileid4,file='Concentration.txt')
write(*,*) "集聚系数:"
call Concentration()
open(fileid5,file='shortPath.txt')
write(*,*) "请输入两个节点(不大于",N+M,")"
read(*,*) node1,node2
call shortPath(node1,node2)
deallocate(er_matrix)
deallocate(degree)
deallocate(E)
deallocate(C)
stop
end program main
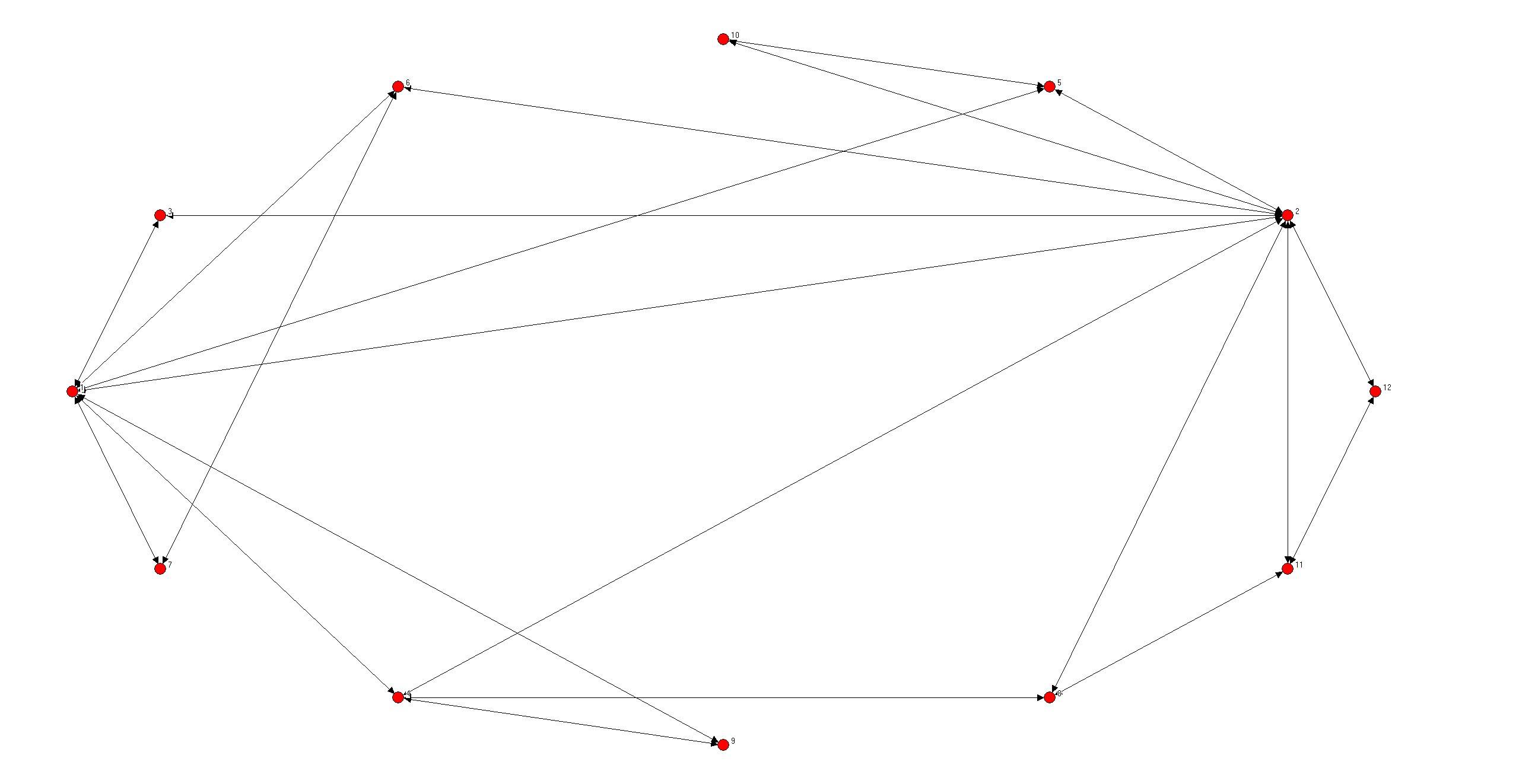







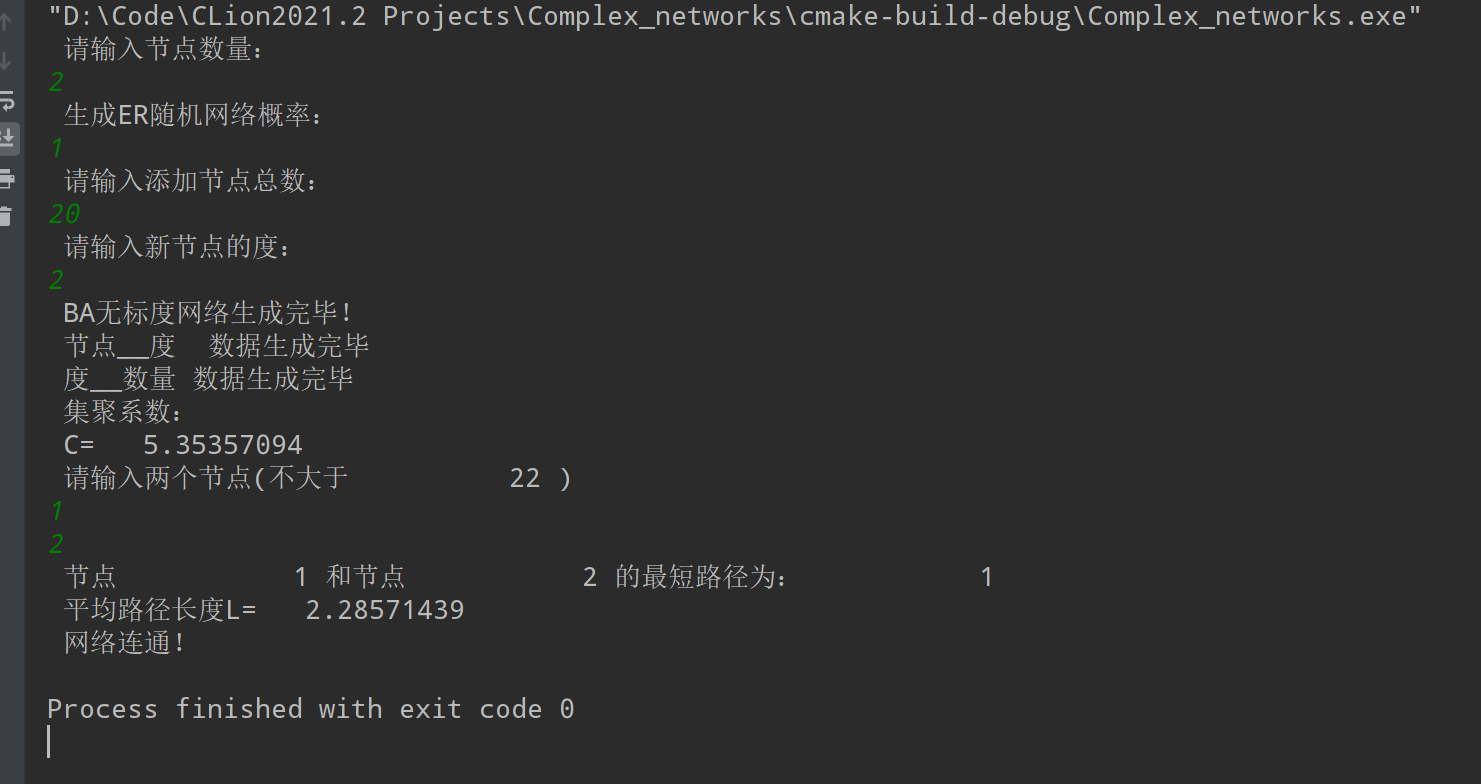

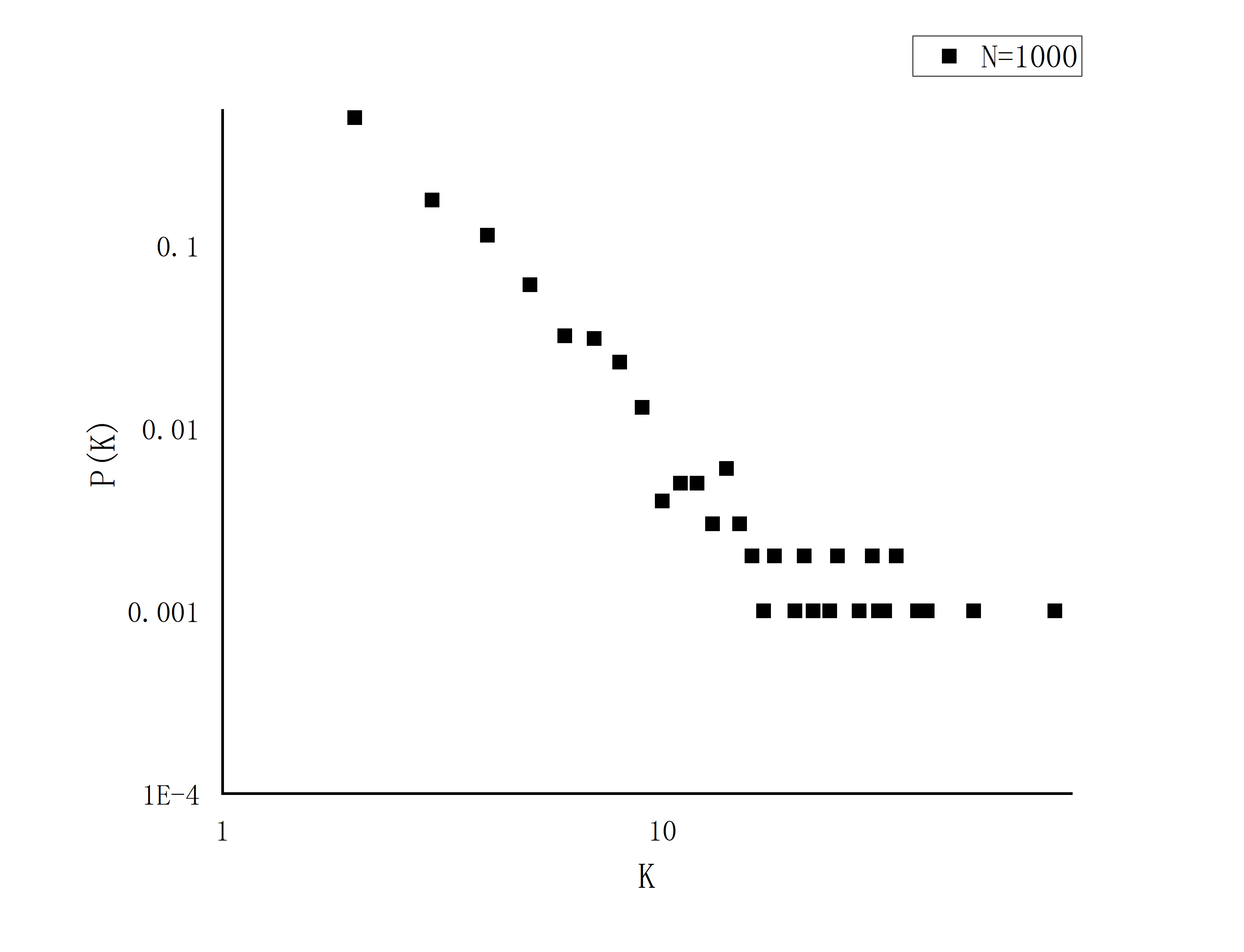
- 基本服从幂律分布









Price有向无标度网络模型
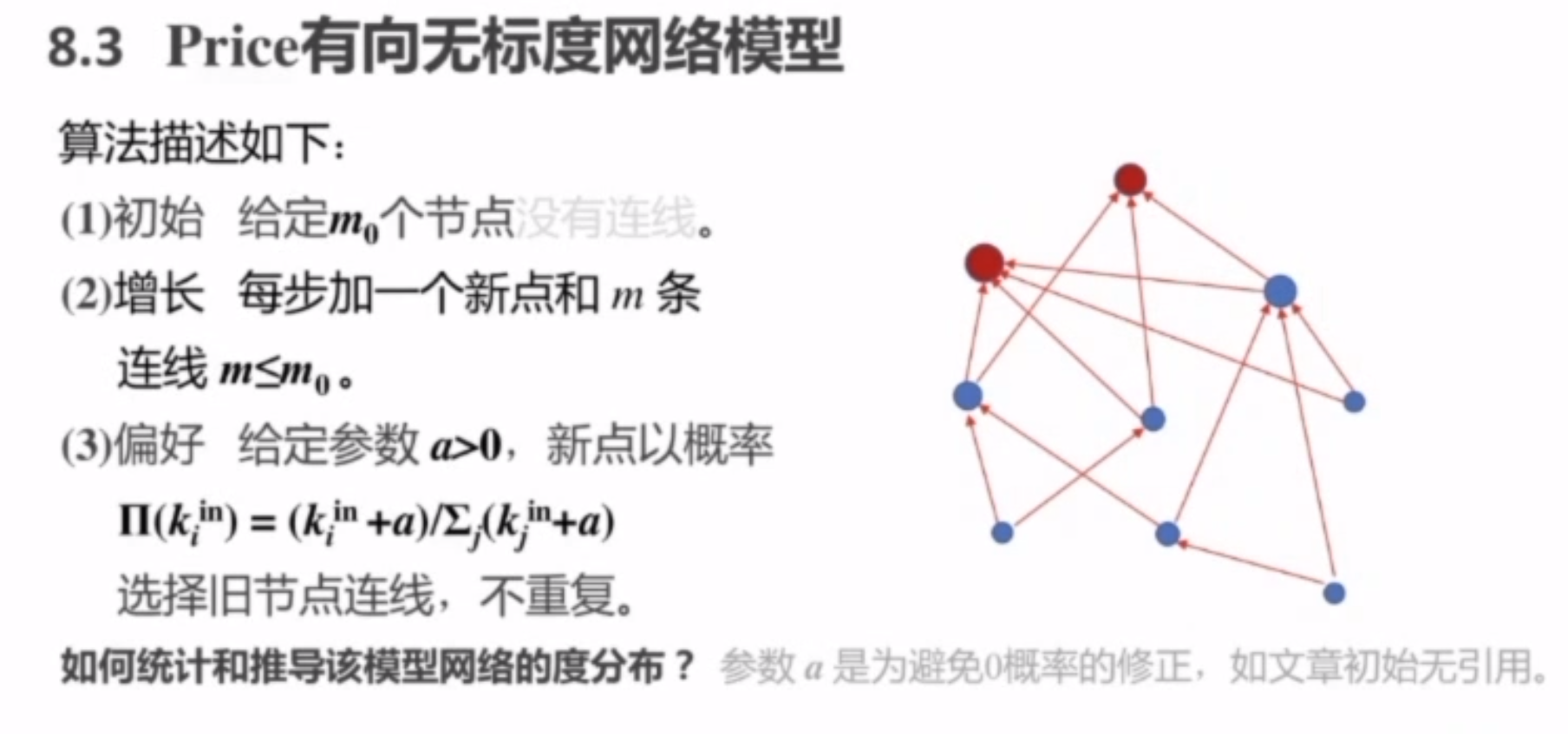




体现偏好连接的节点复制模型


BB适应度网络模型

局域世界演化网络模型


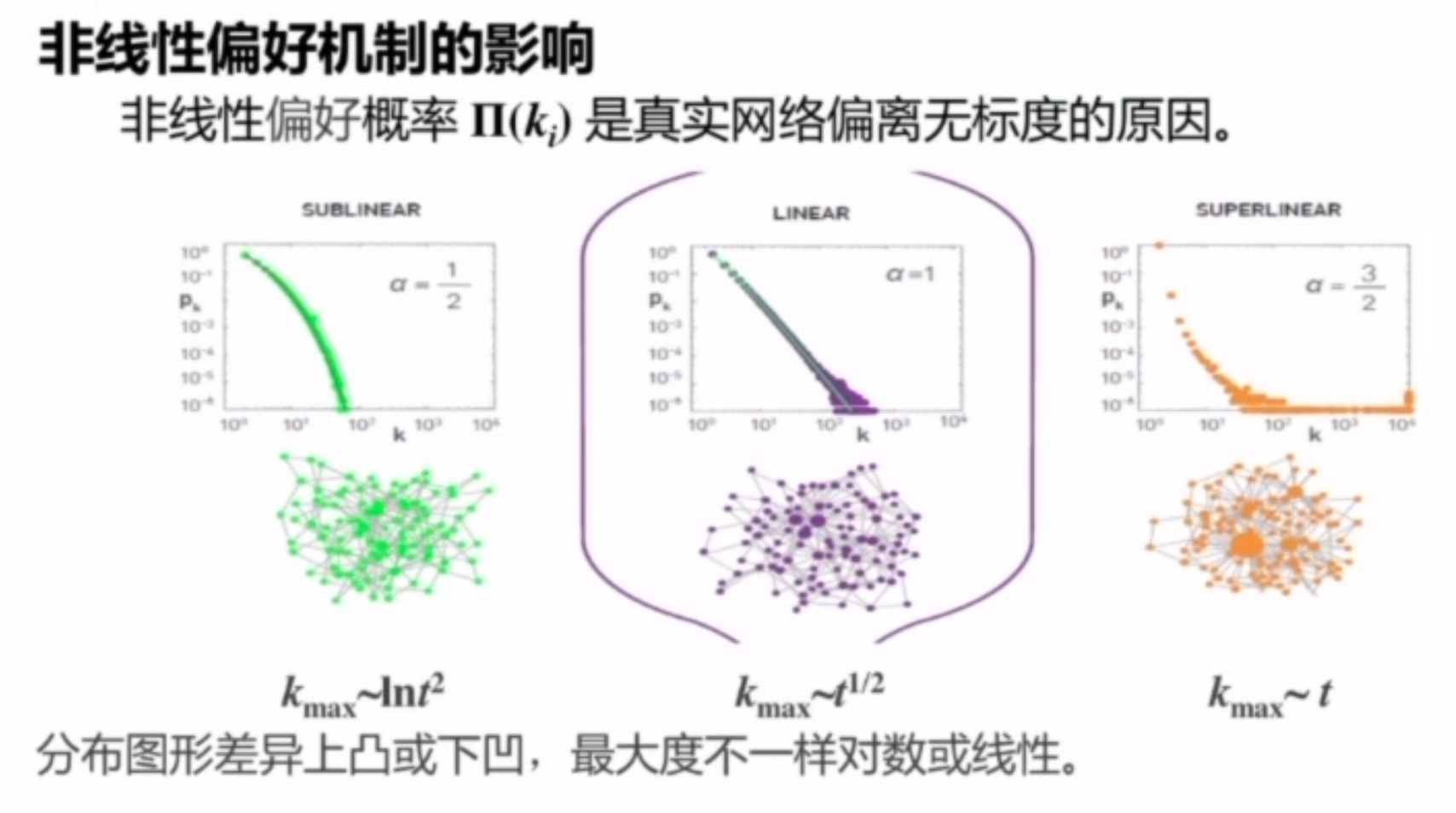
AB
- 由
Barabasi和Albert提出的标准模型,可以生成任意幂律指数的无标度网络。
小结


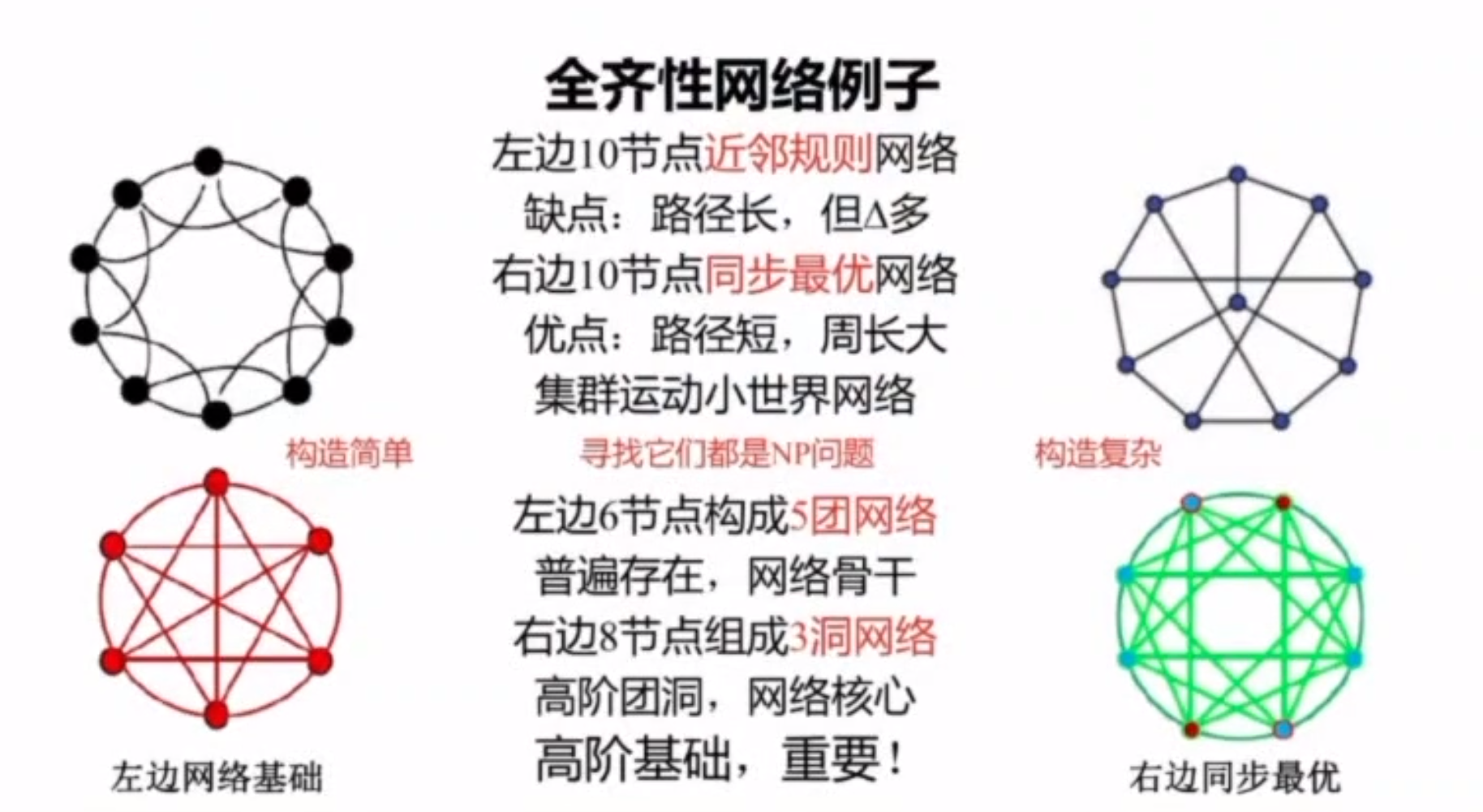

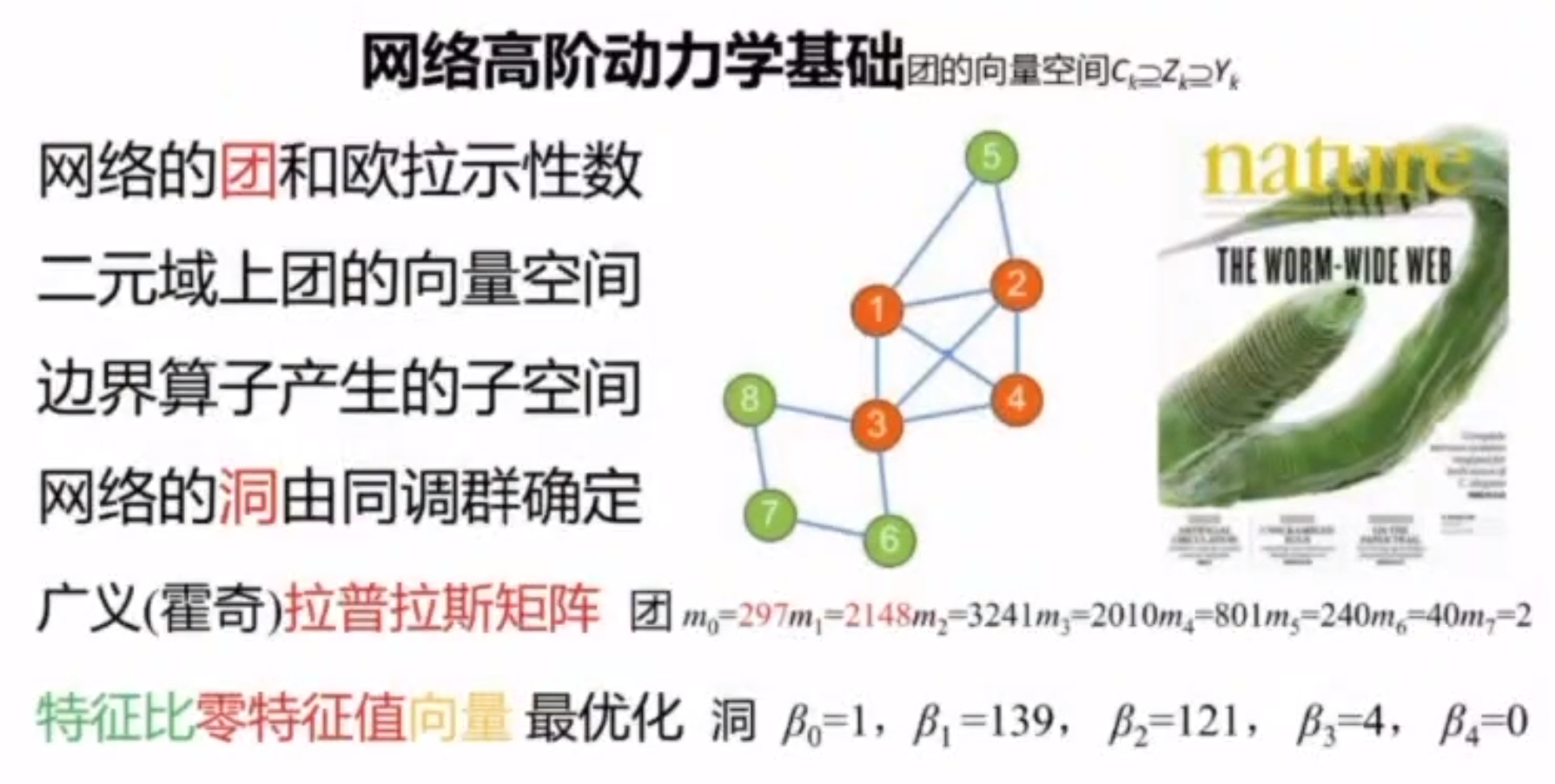

指数随机图模型
exponential random graph models社会网络学者常用的刻画网络结构时变的复杂社会网络模型。
自适应网络
Adaptive Network
空间网络
Spatial Networks
网络的网络
Networks of Networks
时效网络
Temporal Networks
图论

哥尼斯堡的桥
- 难题:不重复走过每座桥

- 启发:不重复经历每条边,就需要起点和终点的度为奇数
网络和图
在科技文献中,网络和图一般不区分地交替使用
网络由节点数N和链接数L来刻画
度、平均度和度分布








k表示度数,Pk是度为k的概率,可以看到,度越大,其该度出现的概率越小。- 度分布通常画在双对数坐标下,也可以直接绘制
lnPk关于lnk的函数。
邻接矩阵



真实网络是稀疏的



加权网络



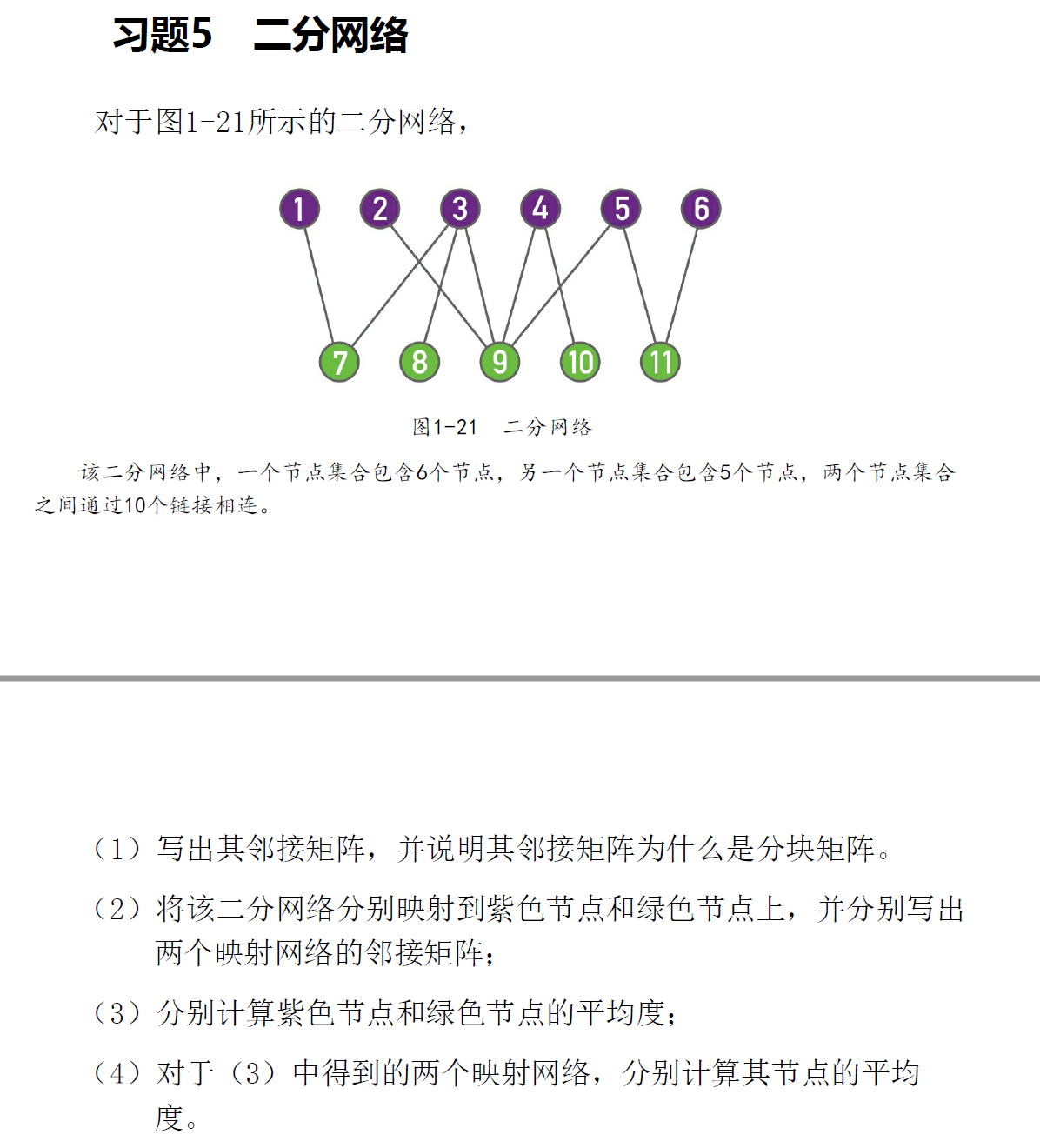
二分网络



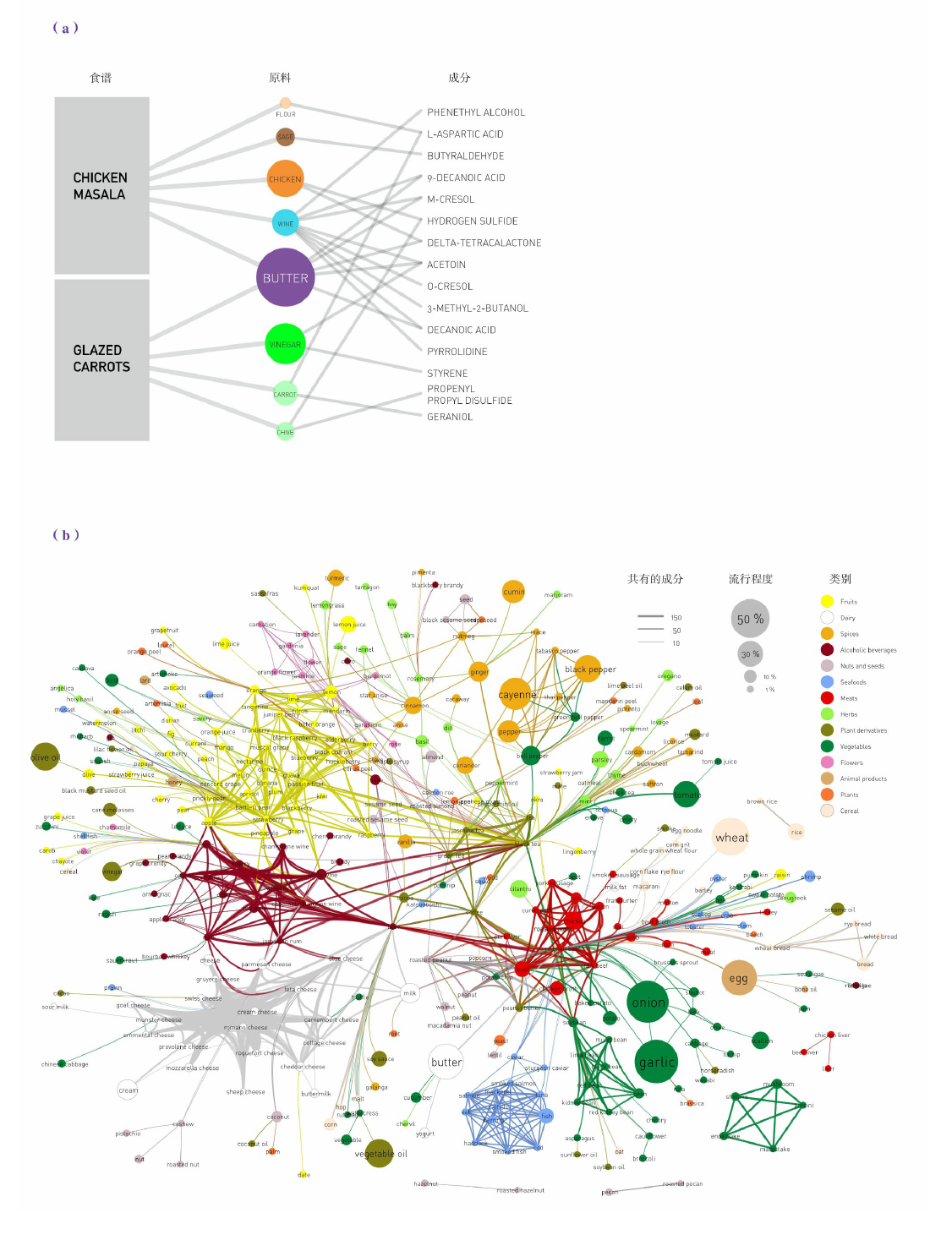

路径和距离

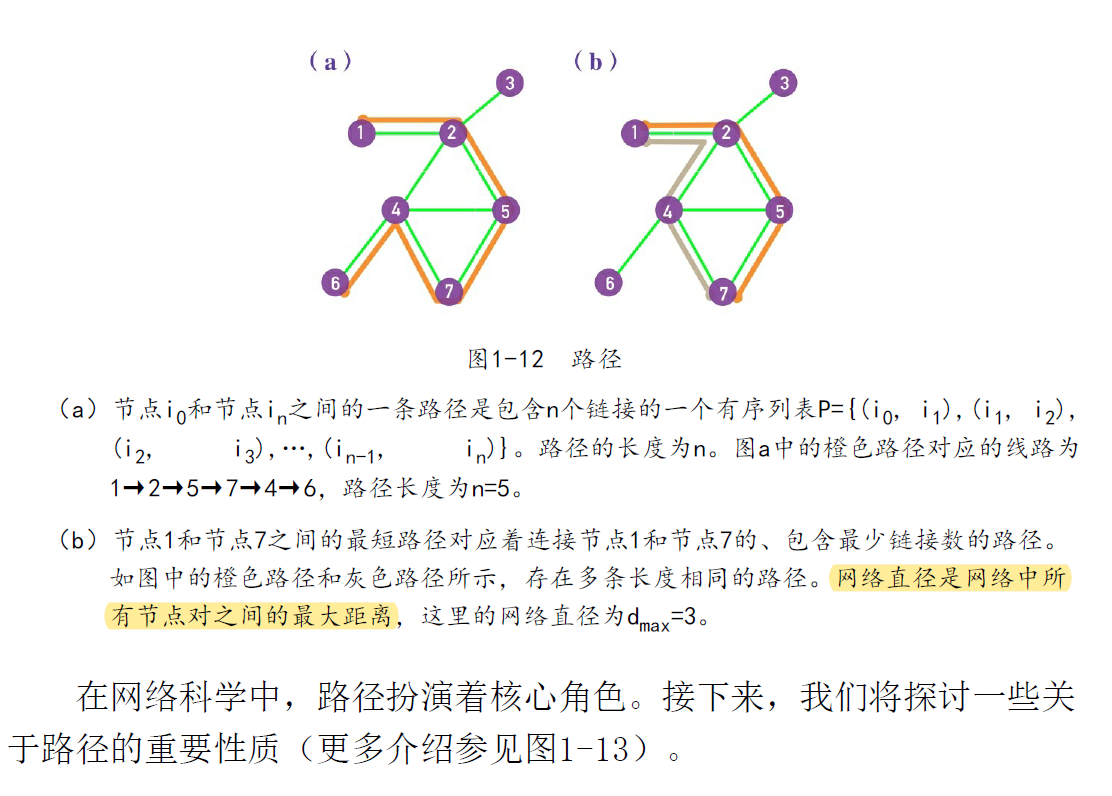
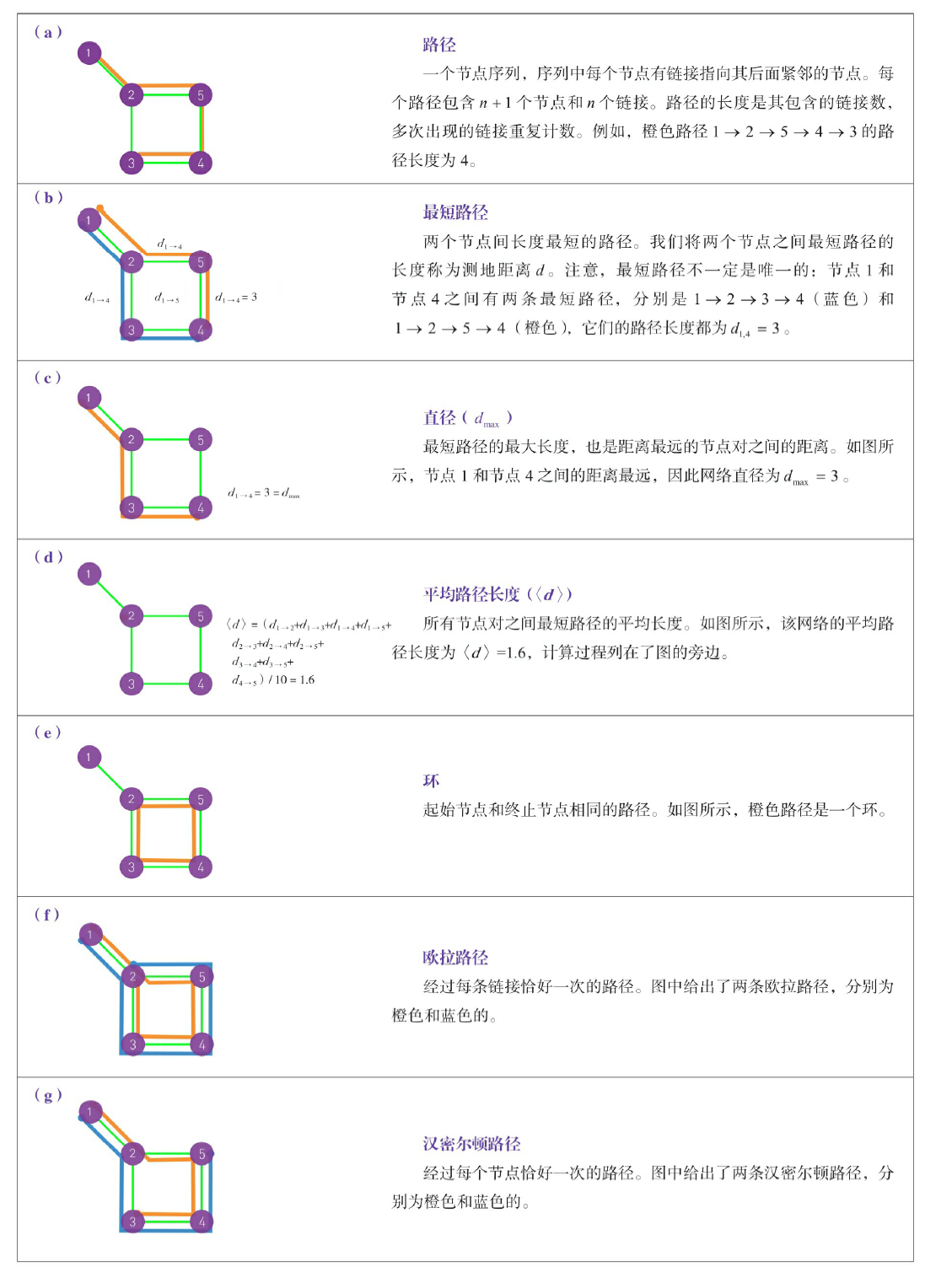








连通性

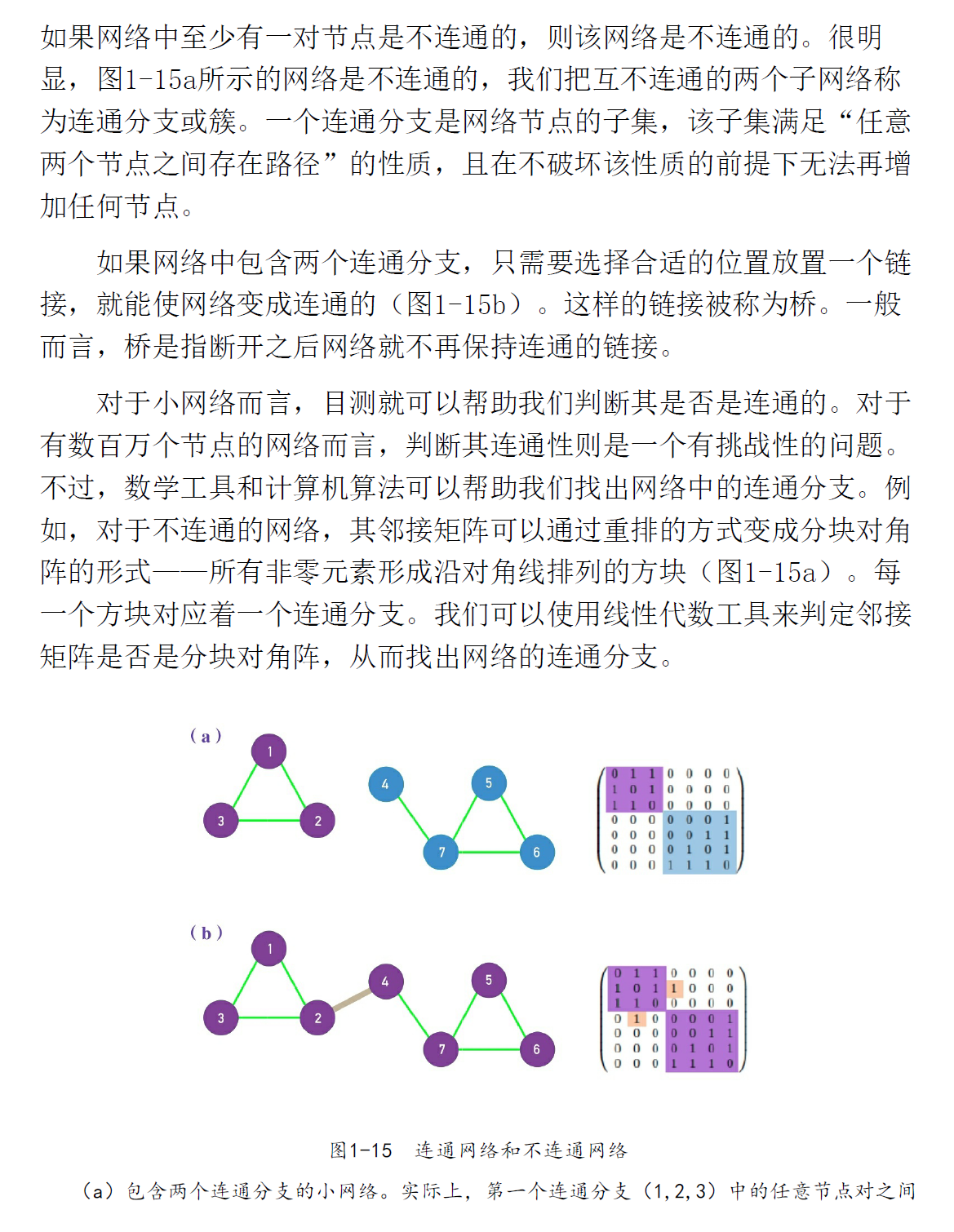


集聚系数

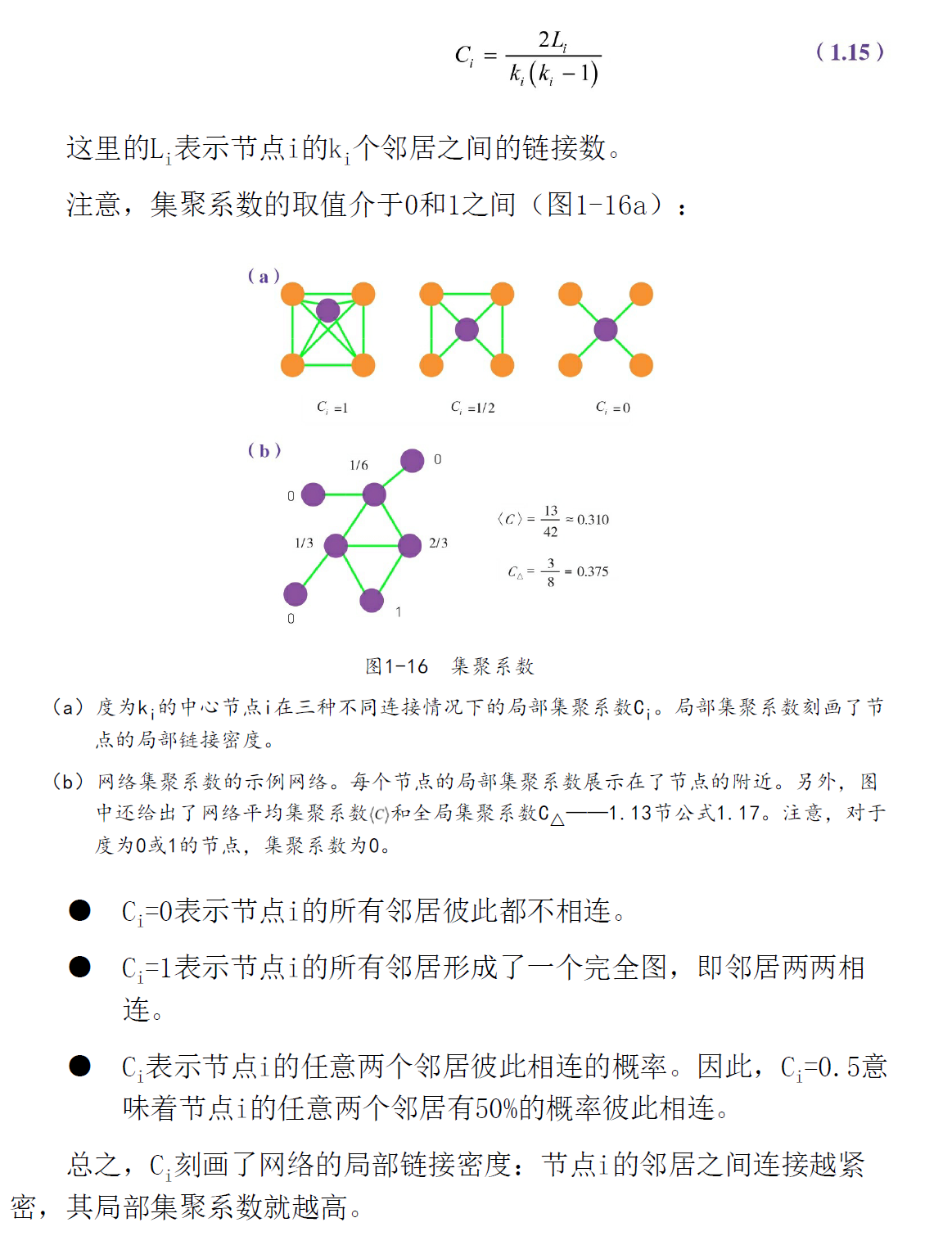

(a)的Ki的节点i的度为4,完全图时,节点i的邻居节点都相连,即Li为6
小结

课后习题
习题一

- 解答:
a图可以直接一笔画出,开始节点与终止节点的度必为奇数
习题二

- 解答:
- 矩阵的迹是指一个n×n矩阵
A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)
module networks
implicit none
integer,parameter :: fileid = 10
integer,parameter :: number = 10
contains
subroutine sub1()
implicit none
integer :: i,j,k,m
integer :: matrix_A(number,number)
integer :: det_I(1,number),det_I_Transpose(number,1)
integer :: limit_K(number,1),Knn(number),knnn(number),Knn_Transpose(number,1)
integer :: L(1,1),n=0,ans(1,number),answer(1,1)=0,ans1(1,number),answer1(1,1)=0
real :: x
matrix_A = 0
det_I=1
Knn_Transpose=1
!创建一个无向无权无自环网络的邻接矩阵
call random_seed()
do i=number,2,-1
do j=i-1,1,-1
!产生随机数
call random_number(x)
if(x>0.5) then
matrix_A(j,i)=1
matrix_A(i,j)=1
end if
end do
end do
!转置行向量为列向量
det_I_Transpose=transpose(det_I) !转置transpose(A)
!各元素的度K
limit_K=matmul(matrix_A,det_I_Transpose) !矩阵相乘matmul(A,B)
!网络中链接总数L
L=matmul(det_I,limit_K)
!网络中三角形个数T
do i=1,number-1,1
do j=number,i+1,-1
do n=1,number-i-1,1
if(j-n<3) continue
if(matrix_A(i,j)==1.and.matrix_A(i,j-n)==1.and.matrix_A(j,j-n)==1) then
if(i<j.and.i<j-n) then
write(*,*) i,j,j-n
end if
end if
end do
end do
end do
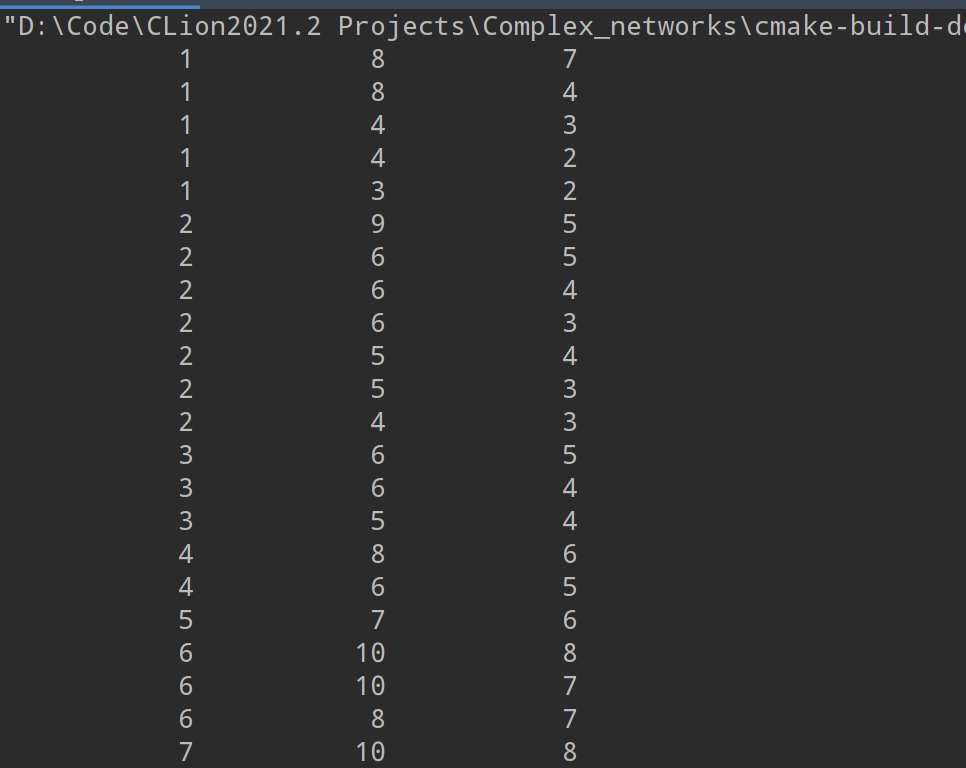
!向量Knn:第i个元素为节点i的邻居节点的度之和
do i=1,number,1
do j=1,number,1
if(matrix_A(i,j)==1) then
do k=1,number,1
ans(1,k) = matrix_A(j,k)
end do
answer=answer+matmul(ans,Knn_Transpose)
end if
end do
Knn(i)=answer(1,1)
answer(1,1)=0
end do
!向量Knnn:第i个元素为节点i的二阶邻居节点的度之和
do i=1,number,1
do j=1,number,1
if(matrix_A(i,j)==1) then
do k=1,number,1
if(matrix_A(j,k)==1) then
do m=1,number,1
ans1(1,m) = matrix_A(k,m)
end do
answer1=answer1+matmul(ans1,Knn_Transpose)
end if
end do
end if
end do
Knnn(i)=answer1(1,1)
answer1(1,1)=0
end do
open(unit=fileid,file="matrix_A.txt")
!输出矩阵
do i=1,number,1
do j=1,number,1
write(fileid,"(I2)",advance='no') matrix_A(i,j)
end do
write(fileid,*)
end do
write(*,*) matrix_A
write(*,*) limit_K
write(*,*) L
write(*,*) Knn
write(*,*) Knnn
return
end subroutine sub1
end module networks
program Complex_networks
use networks
implicit none
call sub1
stop
end program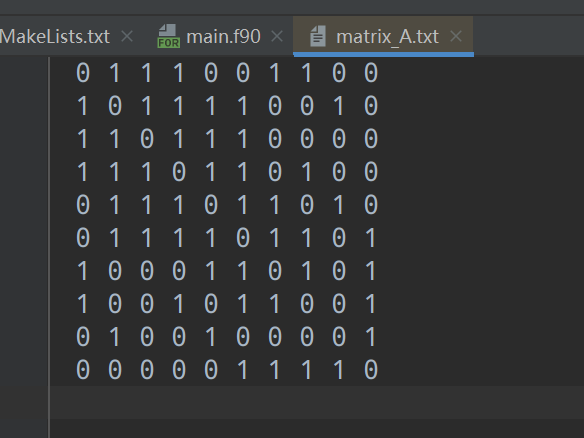
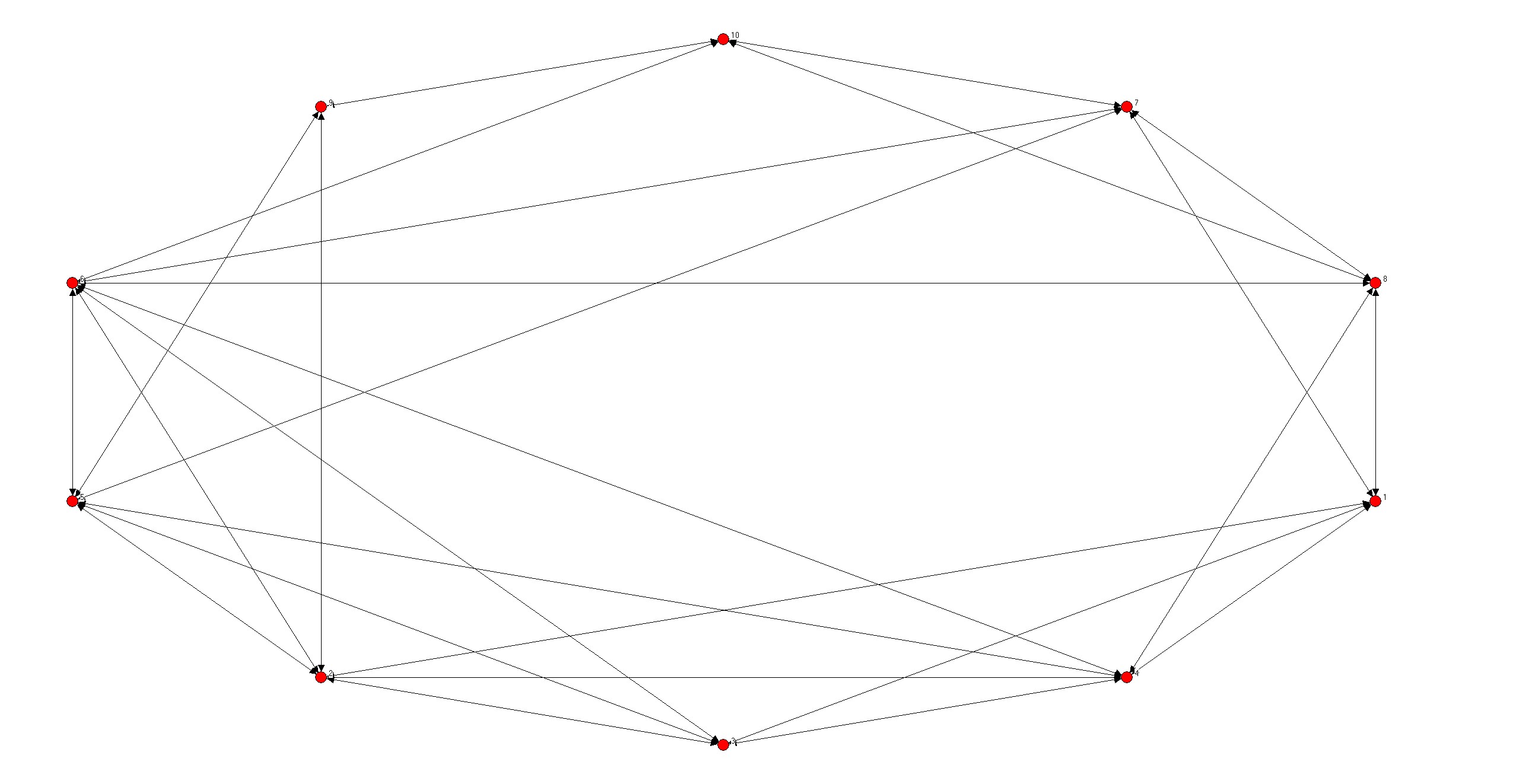

- 第四问,不知道如何求矩阵的迹,使用循环判断的方法。
习题三


习题四

习题五
习题六

随机网络
随机网络模型
- 定义


- 构建随机网络的步骤如下

N个节点的无向图有N(N-1)/2条链边,即(N-1)+(N-2)...+1
链接数





度分布








随机网络的演化









真实网络是超临界的



小世界










聚集系数





小结:真实网络不是随机的




课后习题
习题一 埃尔德什——雷尼网络

习题二 生成埃尔德什——雷尼网络

习题三 环形网络


习题四 凯莱树

习题五 “势利”网络

习题六 “势利”社交网络




