Robustness of chimera states for coupled FitzHugh-Nagumo oscillators
阅读
- 下载地址:https://chinazhang-my.sharepoint.com/:b:/g/personal/rep_rebirth_zh_zhangwenhao_icu/Eablmt92oDpEhswILBf7BZcBz8AJK1Hu6jgV5M3hYlgg8w?e=bFBgaA
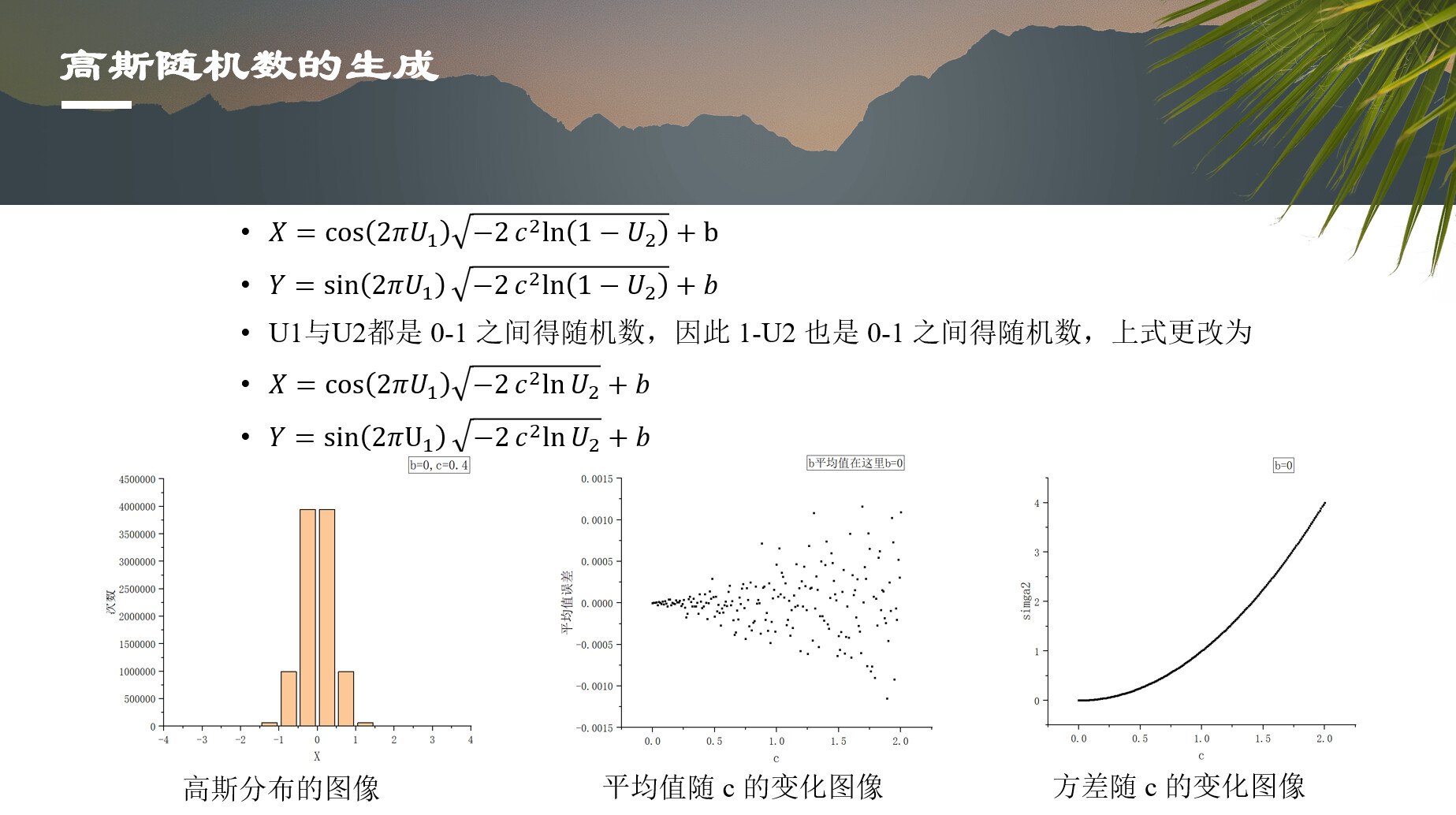
- 高斯分布(正态分布)随机数生成
复现
figure 1
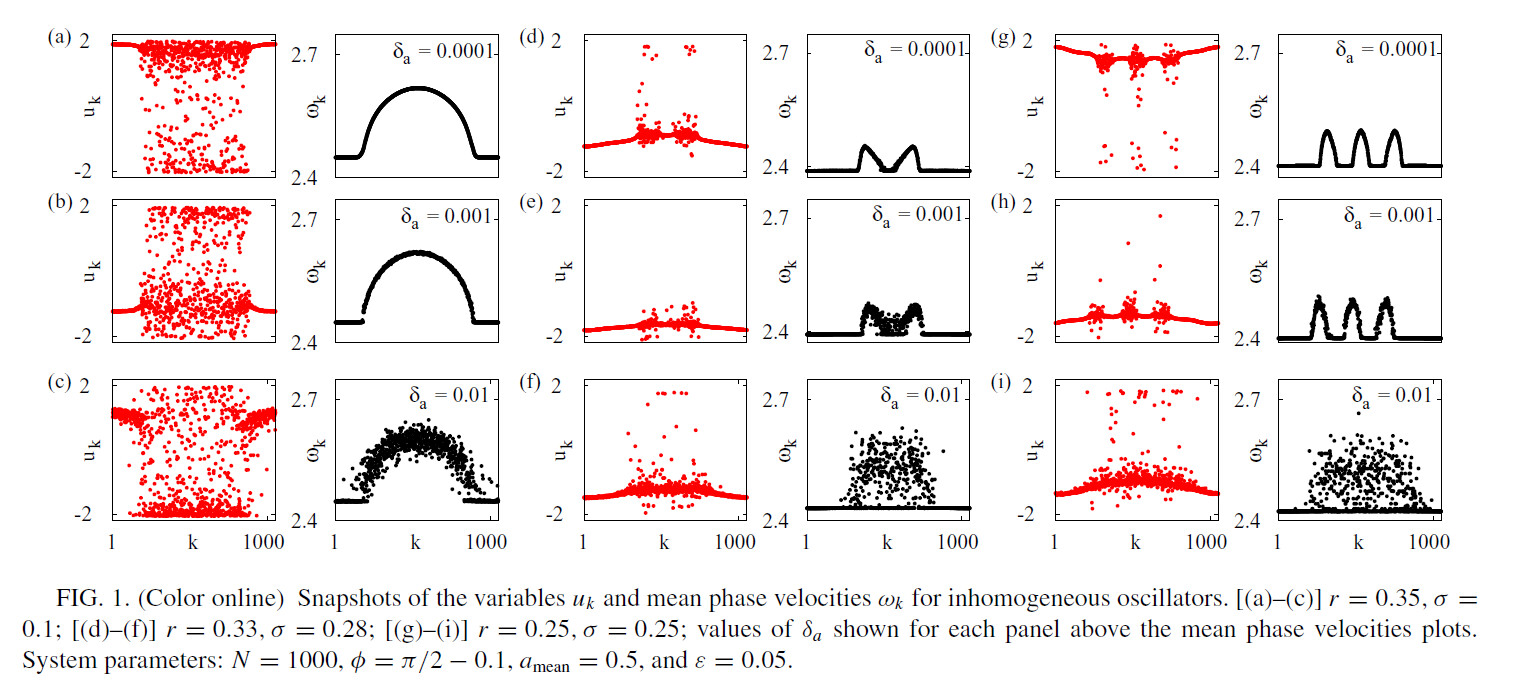
figure 1_A
- r=0.35,sigma=0.1,delte_a=0.0001
module FHN
implicit none
real,parameter :: h=0.02D0,PI=3.1415926D0
integer,parameter :: N=1000,MaxT=100000
integer,allocatable :: neighbour_matrix(:,:)
real :: u(N),v(N)
contains
subroutine u0_v0()
implicit none
integer :: k
real :: x1,x2
do k=1,N,1
!100 call random_number(x1)
! call random_number(x2)
! if(abs((4.0*x1-2.0)**2+(4.0*x2-2.0)**2-4.0)<=0.01) then
! u(k)=4.0*x1-2.0
! v(k)=4.0*x2-2.0
! else
! goto 100
! end if
! write(10,*) u(k),v(k)
read(10,*) u(k),v(k)
end do
end subroutine u0_v0
subroutine fnf(p,sigma)
implicit none
integer :: k,i,j,t,p,count_number(N) !count_number 环数
real :: func_u(N),func_v(N),epsilon=0.05D0,gamma=0.7D0,beta=0.0001D0,sigma,a(N),effect_u,effect_v,&
&b_uu,b_uv,b_vu,b_vv,t_up(N),t_down(N),t_each(N),omega(N)
a=0.0
count_number=0
t_up=0.0
t_down=0.0
t_each=0.0
omega=0.0
b_uu=cos(PI/2.0-0.1)
b_uv=sin(PI/2.0-0.1)
b_vu=-b_uv
b_vv=b_uu
! call Gaussian(a)
do k=1,N
read(30,*) a(k)
end do
do t=1,MaxT,1
do k=1,N,1
effect_u=0.0D0
effect_v=0.0D0
do j=1,N,1
effect_u=effect_u+neighbour_matrix(k,j)*(b_uu*(u(j)-u(k))+b_uv*(v(j)-v(k)))
effect_v=effect_v+neighbour_matrix(k,j)*(b_vu*(u(j)-u(k))+b_vv*(v(j)-v(k)))
end do
func_u(k)=u(k)+h*((u(k)-(u(k)**3)/3.0-v(k)+sigma/(2.0*p)*effect_u)/epsilon)
func_v(k)=v(k)+h*(u(k)+a(k)+sigma/(2.0*p)*effect_v)
if(t==MaxT) then
write(20,*) k,u(k)
end if
if(t>50000) then
if(k==500) then
write(40,*) u(k),v(k)
end if
if(v(k)>0.5.and.func_v(k)<0.5) then
count_number(k)=count_number(k)+1
if(count_number(k)>1) then
t_each(k)=t_each(k)+t*h-t_down(K)
end if
t_down(k)=t*h
end if
end if
end do
u=func_u
v=func_v
if(t==MaxT) then
do i=1,N,1
omega(i)=2.0*PI*((count_number(i)-1)/t_each(i))
write(50,*) i,omega(i)
write(*,*) i,t_each(i),omega(i),count_number(i)
write(60,*) u(i),v(i)
end do
end if
end do
return
end subroutine fnf
!建立网状结构
subroutine neighbour(K)
implicit none
integer :: K !单节点K个邻居
integer :: i,j,number
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
return
end subroutine neighbour
!生成高斯分布(正态分布)的随机数a(k)
subroutine Gaussian(a)
implicit none
integer :: k
real :: x1,x2,a(N),delte_a,a_mean
delte_a=0.0001D0
a_mean=0.5
do k=1,N
call random_number(x1)
call random_number(x2)
a(k)=cos(2.0*PI*x2)*sqrt(-2.0*delte_a**2*log(x1))+a_mean
end do
return
end subroutine Gaussian
end module FHN
program main
use FHN
implicit none
integer :: p
real :: sigma,r
open(10,file="data_u0_v0.txt")
open(20,file="data_k_u.txt")
open(30,file="data_ak.txt")
open(40,file="data_t_u.txt")
open(50,file="data_k_omega.txt")
open(60,file="data.txt")
call random_seed()
call u0_v0()
write(*,*) "请输入耦合半径r和耦合强度σ:"
read(*,*) r,sigma
p=nint(r*N)
write(*,*) p,sigma,r
call neighbour(2*p)
call fnf(p,sigma)
deallocate(neighbour_matrix)
close(10)
close(20)
close(30)
close(40)
close(50)
close(60)
end program main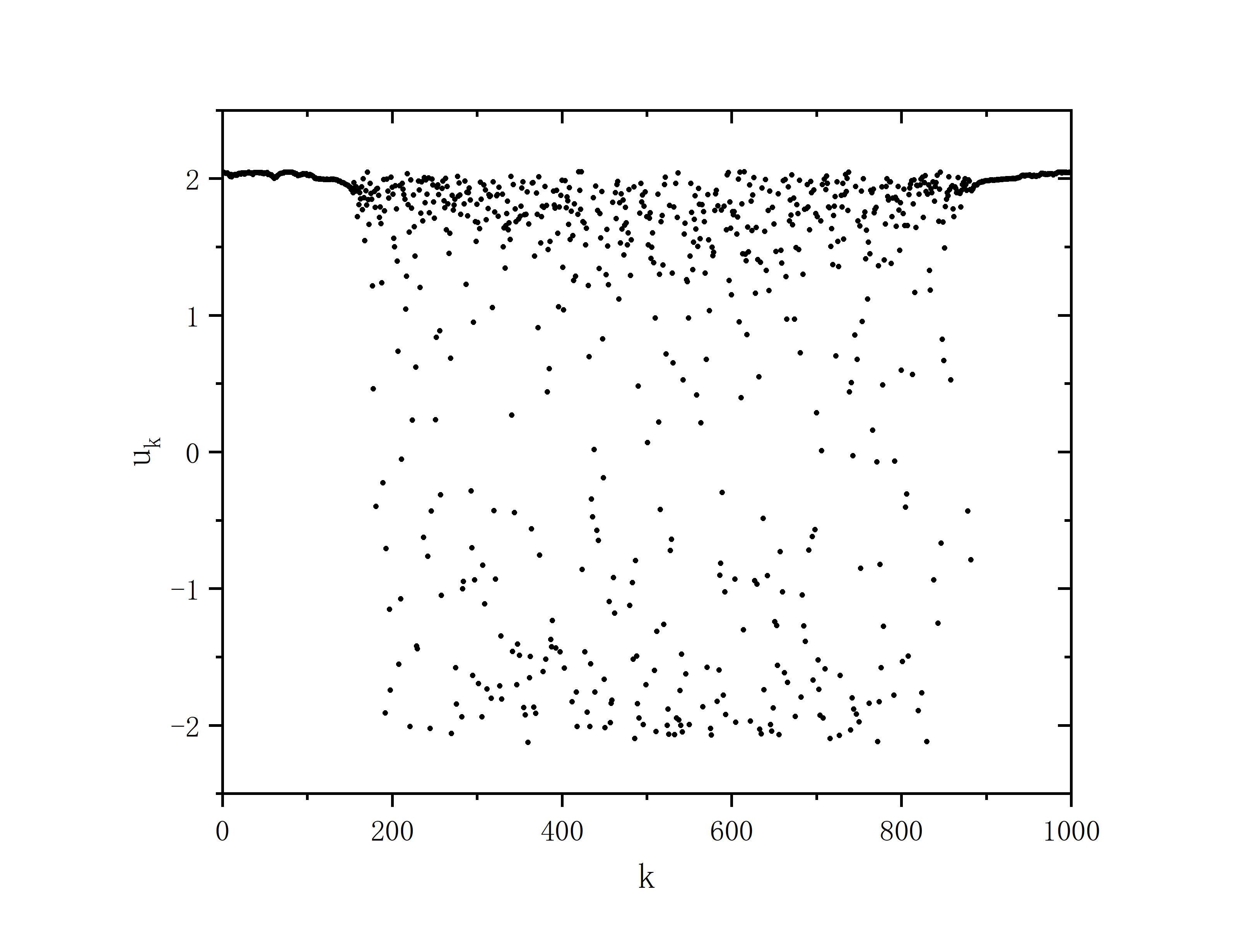
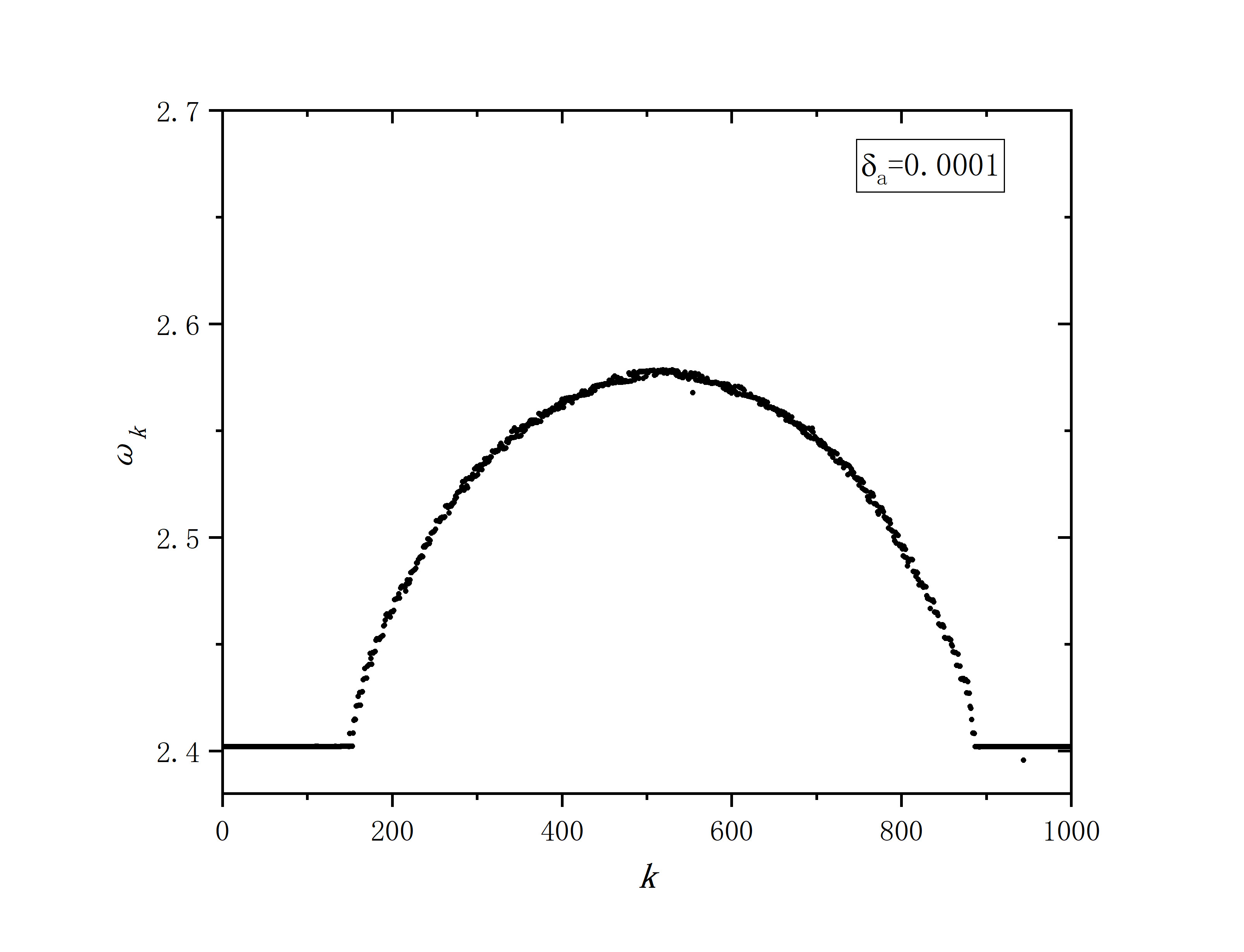
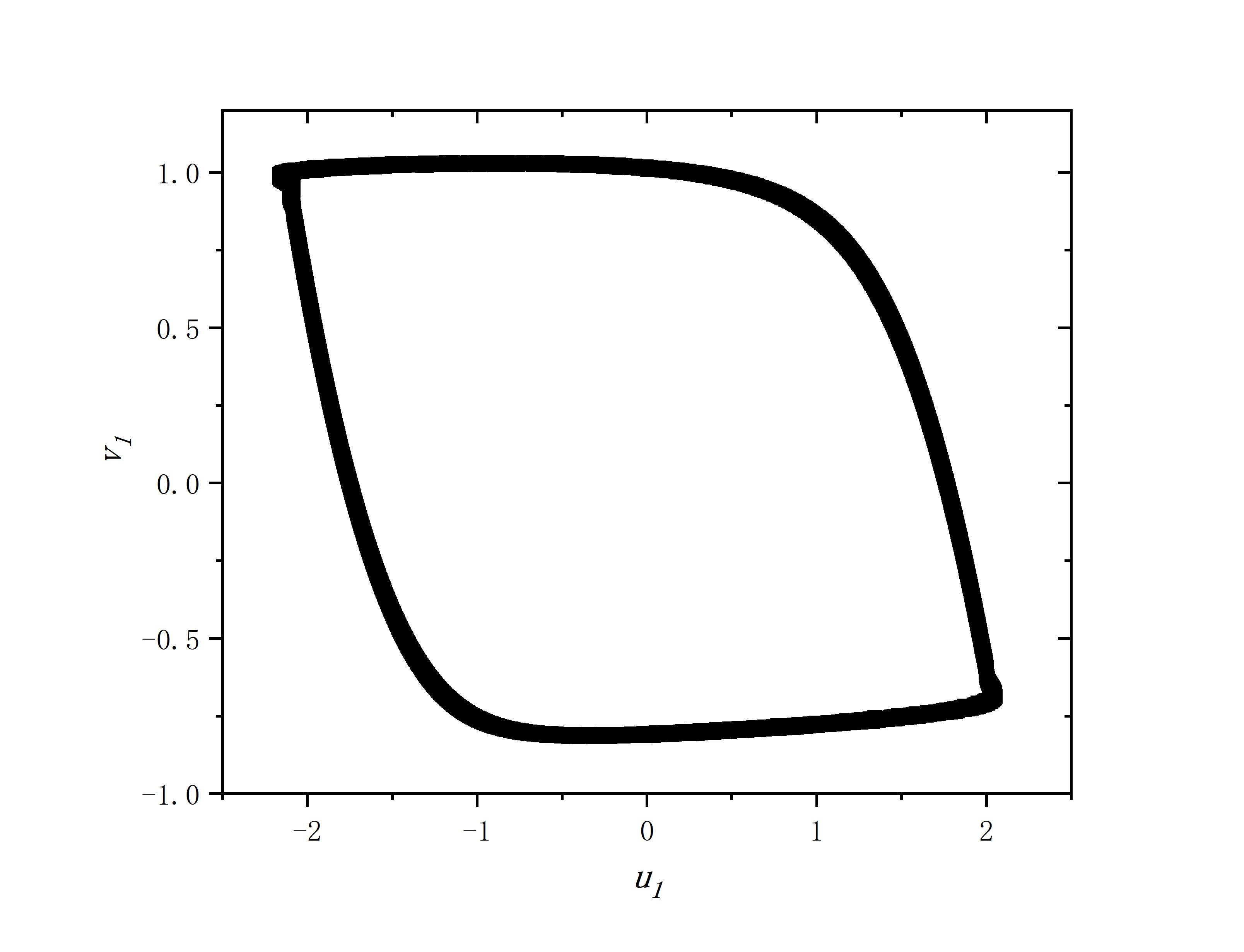

figure 1_B
- r=0.35,sigma=0.1,delte_a=0.001
module FHN
implicit none
real,parameter :: h=0.02D0,PI=3.1415926D0
integer,parameter :: N=1000,MaxT=100000
integer,allocatable :: neighbour_matrix(:,:)
real :: u(N),v(N)
contains
subroutine u0_v0()
implicit none
integer :: k
real :: x1,x2
do k=1,N,1
!100 call random_number(x1)
! call random_number(x2)
! if(abs((4.0*x1-2.0)**2+(4.0*x2-2.0)**2-4.0)<=0.01) then
! u(k)=4.0*x1-2.0
! v(k)=4.0*x2-2.0
! else
! goto 100
! end if
! write(10,*) u(k),v(k)
read(10,*) u(k),v(k)
end do
end subroutine u0_v0
subroutine fnf(p,sigma)
implicit none
integer :: k,i,j,t,p,count_number(N) !count_number 环数
real :: func_u(N),func_v(N),epsilon=0.05D0,gamma=0.7D0,beta=0.0001D0,sigma,a(N),effect_u,effect_v,&
&b_uu,b_uv,b_vu,b_vv,t_up(N),t_down(N),t_each(N),omega(N)
a=0.0
count_number=0
t_up=0.0
t_down=0.0
t_each=0.0
omega=0.0
b_uu=cos(PI/2.0-0.1)
b_uv=sin(PI/2.0-0.1)
b_vu=-b_uv
b_vv=b_uu
call Gaussian(a)
do k=1,N
write(30,*) a(k)
end do
do t=1,MaxT,1
do k=1,N,1
effect_u=0.0D0
effect_v=0.0D0
do j=1,N,1
effect_u=effect_u+neighbour_matrix(k,j)*(b_uu*(u(j)-u(k))+b_uv*(v(j)-v(k)))
effect_v=effect_v+neighbour_matrix(k,j)*(b_vu*(u(j)-u(k))+b_vv*(v(j)-v(k)))
end do
func_u(k)=u(k)+h*((u(k)-(u(k)**3)/3.0-v(k)+sigma/(2.0*p)*effect_u)/epsilon)
func_v(k)=v(k)+h*(u(k)+a(k)+sigma/(2.0*p)*effect_v)
if(t==MaxT) then
write(20,*) k,u(k)
end if
if(t>50000) then
if(k==500) then
write(40,*) u(k),v(k)
end if
if(v(k)>0.5.and.func_v(k)<0.5) then
count_number(k)=count_number(k)+1
if(count_number(k)>1) then
t_each(k)=t_each(k)+t*h-t_down(K)
end if
t_down(k)=t*h
end if
end if
end do
u=func_u
v=func_v
if(t==MaxT) then
do i=1,N,1
omega(i)=2.0*PI*((count_number(i)-1)/t_each(i))
write(50,*) i,omega(i)
write(*,*) i,t_each(i),omega(i),count_number(i)
write(60,*) u(i),v(i)
end do
end if
end do
return
end subroutine fnf
!建立网状结构
subroutine neighbour(K)
implicit none
integer :: K !单节点K个邻居
integer :: i,j,number
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
return
end subroutine neighbour
!生成正态分布的随机数a(k)
subroutine Gaussian(a)
implicit none
integer :: k
real :: x1,x2,a(N),delte_a,a_mean
delte_a=0.001D0
a_mean=0.5
do k=1,N
call random_number(x1)
call random_number(x2)
a(k)=cos(2.0*PI*x2)*sqrt(-2.0*delte_a**2*log(x1))+a_mean
end do
return
end subroutine Gaussian
end module FHN
program main
use FHN
implicit none
integer :: p
real :: sigma,r
open(10,file="data_u0_v0_end.txt")
open(20,file="data_k_u.txt")
open(30,file="data_ak.txt")
open(40,file="data_t_u.txt")
open(50,file="data_k_omega.txt")
open(60,file="data.txt")
call random_seed()
call u0_v0()
write(*,*) "请输入耦合半径r和耦合强度σ:"
read(*,*) r,sigma
p=nint(r*N)
write(*,*) p,sigma,r
call neighbour(2*p)
call fnf(p,sigma)
deallocate(neighbour_matrix)
close(10)
close(20)
close(30)
close(40)
close(50)
close(60)
end program main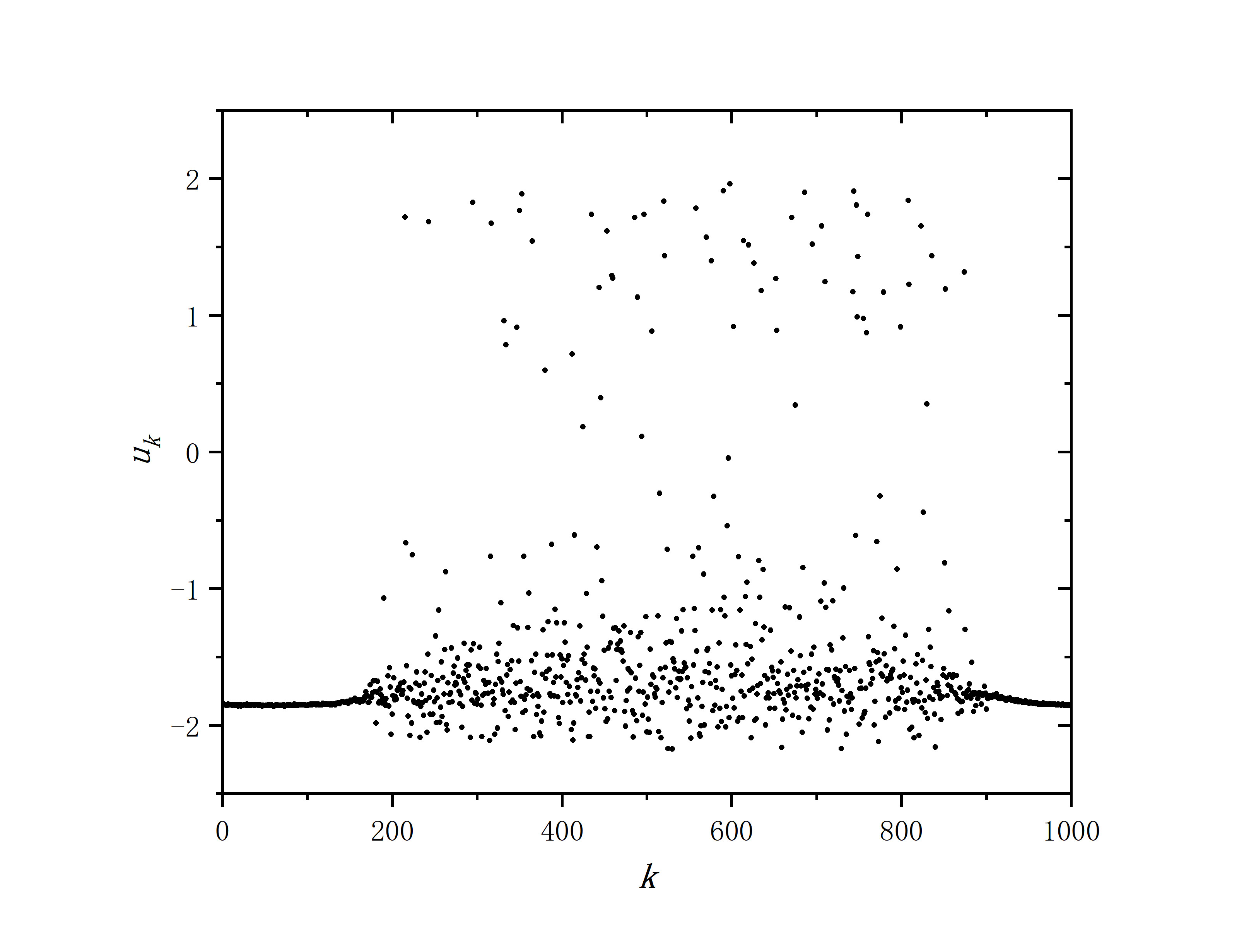

figure 1_C
- r=0.35,sigma=0.1,delte_a=0.01
module FHN
implicit none
real,parameter :: h=0.02D0,PI=3.1415926D0
integer,parameter :: N=1000,MaxT=100000
integer,allocatable :: neighbour_matrix(:,:)
real :: u(N),v(N)
contains
subroutine u0_v0()
implicit none
integer :: k
real :: x1,x2
do k=1,N,1
read(10,*) u(k),v(k)
end do
end subroutine u0_v0
subroutine fnf(p,sigma)
implicit none
integer :: k,i,j,t,p,count_number(N) !count_number 环数
real :: func_u(N),func_v(N),epsilon=0.05D0,gamma=0.7D0,beta=0.0001D0,sigma,a(N),effect_u,effect_v,&
&b_uu,b_uv,b_vu,b_vv,t_up(N),t_down(N),t_each(N),omega(N)
a=0.0
count_number=0
t_up=0.0
t_down=0.0
t_each=0.0
omega=0.0
b_uu=cos(PI/2.0-0.1)
b_uv=sin(PI/2.0-0.1)
b_vu=-b_uv
b_vv=b_uu
call Gaussian(a)
do k=1,N
write(30,*) a(k)
end do
do t=1,MaxT,1
do k=1,N,1
effect_u=0.0D0
effect_v=0.0D0
do j=1,N,1
effect_u=effect_u+neighbour_matrix(k,j)*(b_uu*(u(j)-u(k))+b_uv*(v(j)-v(k)))
effect_v=effect_v+neighbour_matrix(k,j)*(b_vu*(u(j)-u(k))+b_vv*(v(j)-v(k)))
end do
func_u(k)=u(k)+h*((u(k)-(u(k)**3)/3.0-v(k)+sigma/(2.0*p)*effect_u)/epsilon)
func_v(k)=v(k)+h*(u(k)+a(k)+sigma/(2.0*p)*effect_v)
if(t==MaxT) then
write(20,*) k,u(k)
end if
if(t>50000) then
if(k==500) then
write(40,*) u(k),v(k)
end if
if(v(k)>0.5.and.func_v(k)<0.5) then
count_number(k)=count_number(k)+1
if(count_number(k)>1) then
t_each(k)=t_each(k)+t*h-t_down(K)
end if
t_down(k)=t*h
end if
end if
end do
u=func_u
v=func_v
if(t==MaxT) then
do i=1,N,1
omega(i)=2.0*PI*((count_number(i)-1)/t_each(i))
write(50,*) i,omega(i)
write(*,*) i,t_each(i),omega(i),count_number(i)
write(60,*) u(i),v(i)
end do
end if
end do
return
end subroutine fnf
!建立网状结构
subroutine neighbour(K)
implicit none
integer :: K !单节点K个邻居
integer :: i,j,number
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
return
end subroutine neighbour
!生成正态分布的随机数a(k)
subroutine Gaussian(a)
implicit none
integer :: k
real :: x1,x2,a(N),delte_a,a_mean
delte_a=0.01D0
a_mean=0.5
do k=1,N
call random_number(x1)
call random_number(x2)
a(k)=cos(2.0*PI*x2)*sqrt(-2.0*delte_a**2*log(x1))+a_mean
end do
return
end subroutine Gaussian
end module FHN
program main
use FHN
implicit none
integer :: p
real :: sigma,r
open(10,file="data_u0_v0_end.txt")
open(20,file="data_k_u.txt")
open(30,file="data_ak.txt")
open(40,file="data_t_u.txt")
open(50,file="data_k_omega.txt")
open(60,file="data.txt")
call random_seed()
call u0_v0()
write(*,*) "请输入耦合半径r和耦合强度σ:"
read(*,*) r,sigma
p=nint(r*N)
write(*,*) p,sigma,r
call neighbour(2*p)
call fnf(p,sigma)
deallocate(neighbour_matrix)
close(10)
close(20)
close(30)
close(40)
close(50)
close(60)
end program main
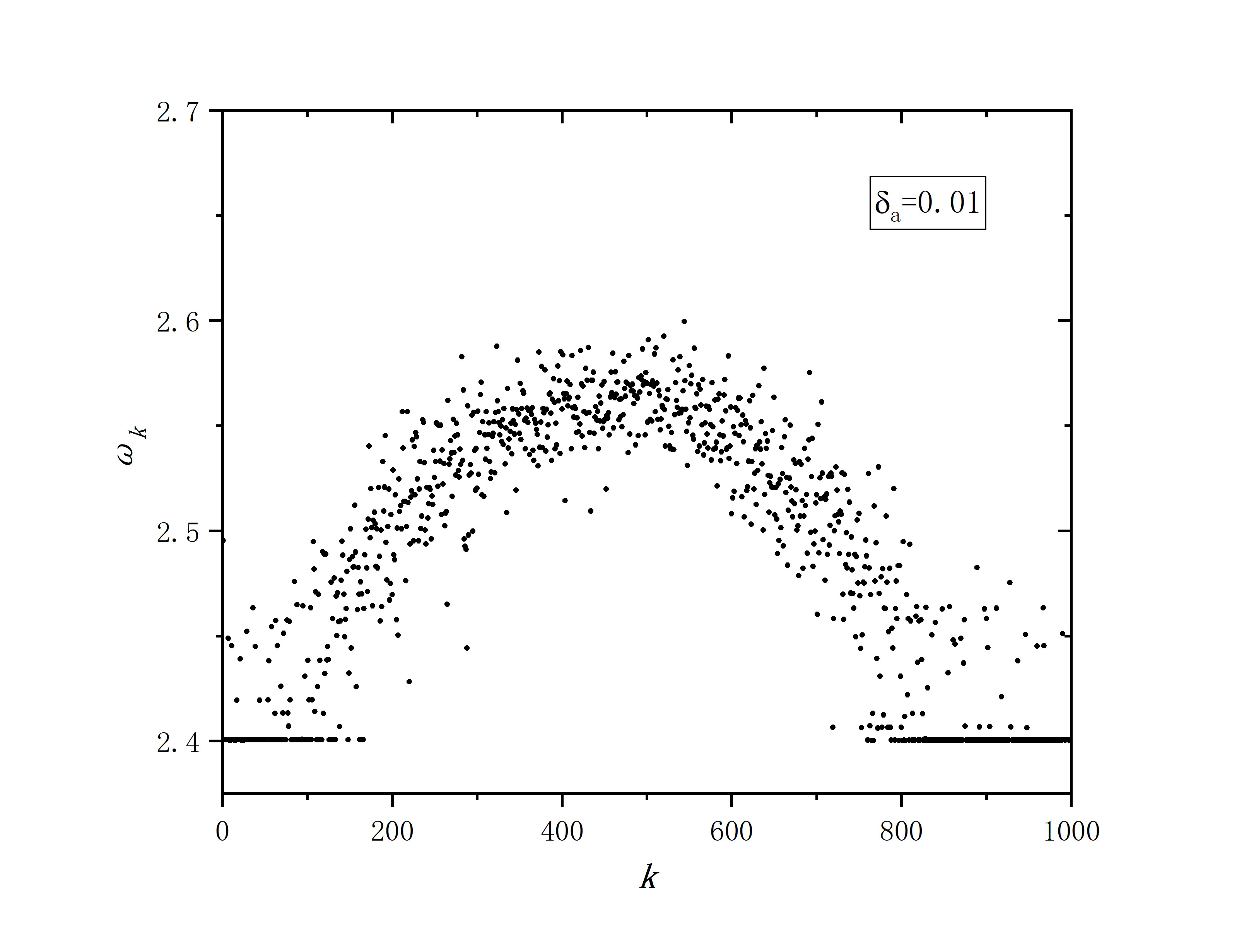
figure 1_D
- r=0.33,sigma=0.28,delte_a=0.0001
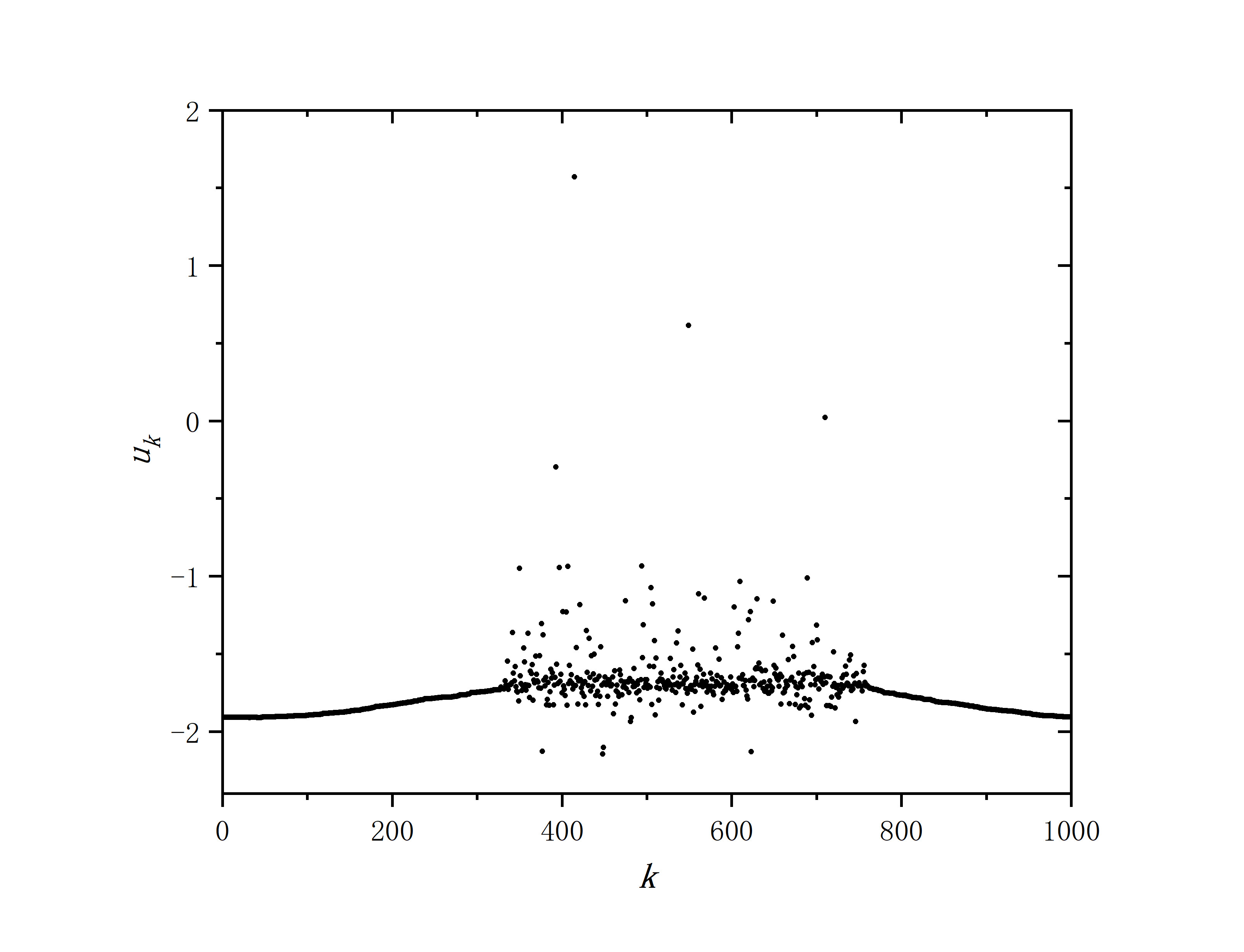

figure 1_E
- r=0.33,sigma=0.28,delte_a=0.001


figure 1_F
- r=0.33,sigma=0.28,delte_a=0.01
 *
*

figure 1_G
- r=0.25,sigma=0.25,delte_a=0.0001


figure 1_H
- r=0.25,sigma=0.25,delte_a=0.001
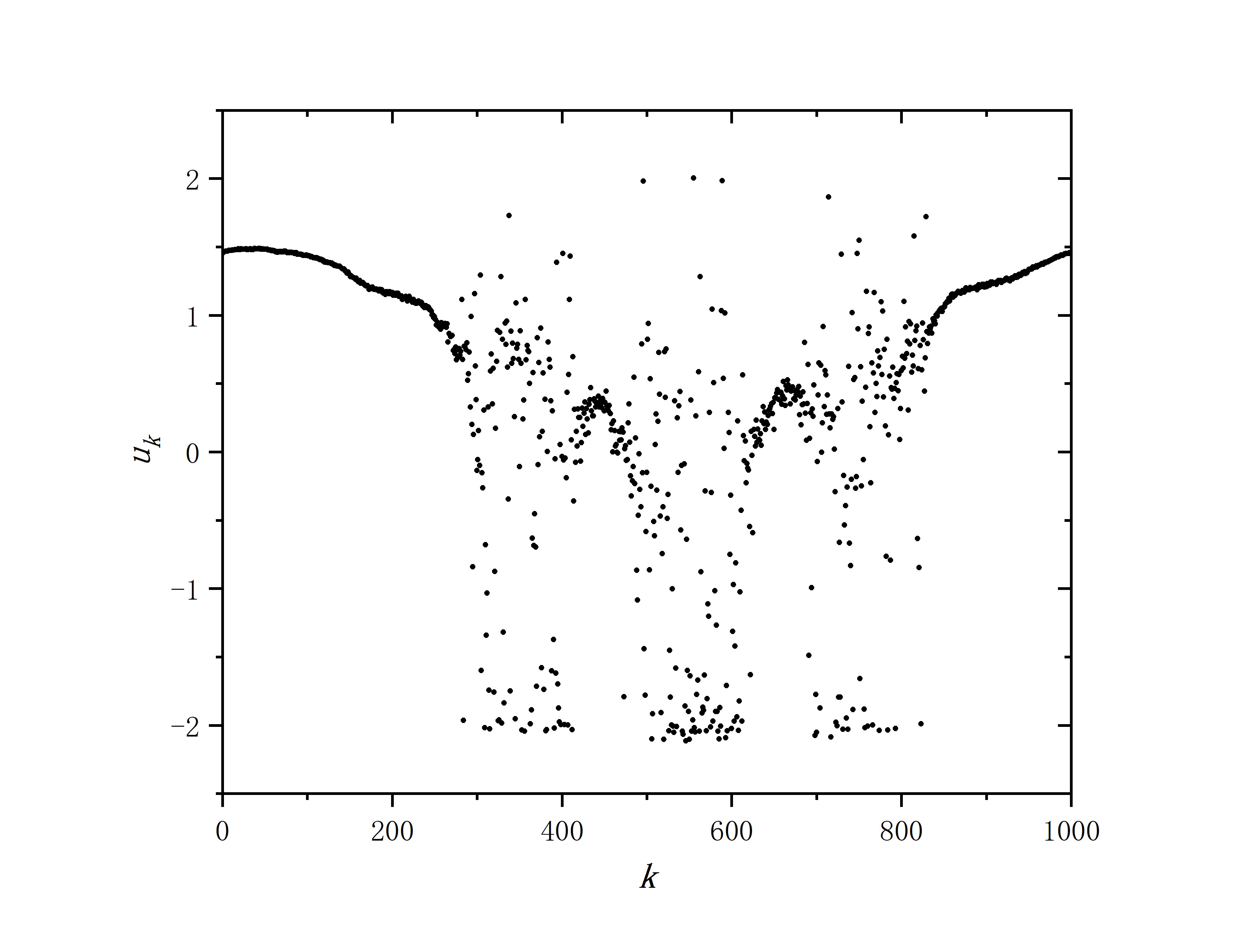

figure 1_I
- r=0.25,sigma=0.25,delte_a=0.01
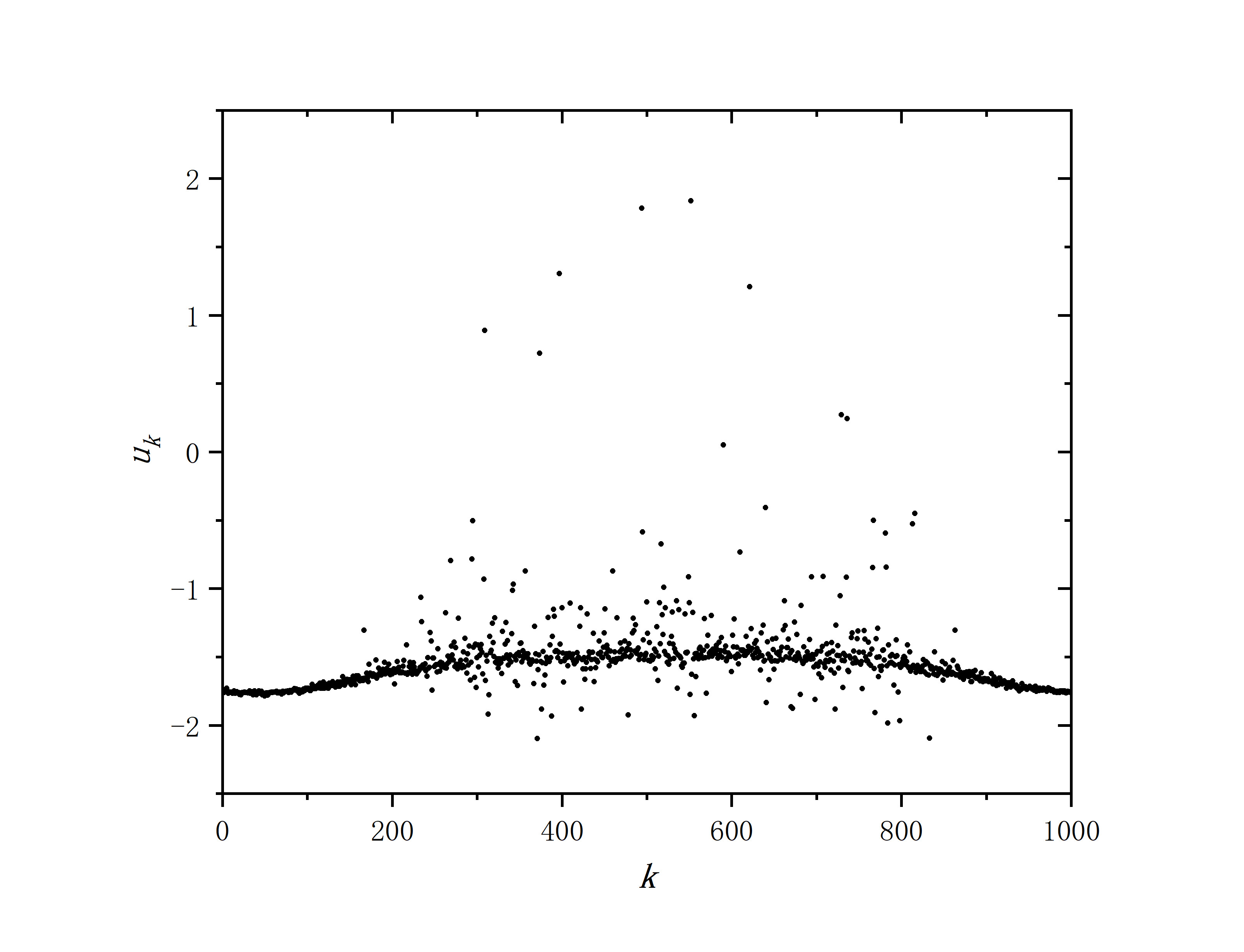

figure 2

module FHN
implicit none
real,parameter :: h=0.02D0,PI=3.1415926D0
integer,parameter :: N=1000,MaxT=50000
integer,allocatable :: neighbour_matrix(:,:)
real :: u(N),v(N)
contains
subroutine u0_v0()
implicit none
integer :: k
open(10,file="data_u0_v0_end.txt")
do k=1,N,1
read(10,*) u(k),v(k)
end do
close(10)
end subroutine u0_v0
subroutine fnf(p,sigma,status)
implicit none
integer :: k,i,j,t,p,num,status,count_number(N) !count_number振荡次数
real :: func_u(N),func_v(N),epsilon=0.05D0,gamma=0.7D0,beta=0.0001D0,sigma,a(N),effect_u,effect_v,&
&b_uu,b_uv,b_vu,b_vv,t_up(N),t_down(N),t_each(N),omega(N),omega_sum(N),omegaMin(N),omegaMax(N)
a=0.0
omegaMin=1000000.0
omegaMax=-1000000.0
b_uu=cos(PI/2.0-0.1)
b_uv=sin(PI/2.0-0.1)
b_vu=-b_uv
b_vv=b_uu
select case(status)
case(1)!黑线
call u0_v0()
a=0.5
count_number=0
t_up=0.0
t_down=0.0
t_each=0.0
omega=0.0
do t=1,MaxT,1
do k=1,N,1
effect_u=0.0D0
effect_v=0.0D0
do j=1,N,1
effect_u=effect_u+neighbour_matrix(k,j)*(b_uu*(u(j)-u(k))+b_uv*(v(j)-v(k)))
effect_v=effect_v+neighbour_matrix(k,j)*(b_vu*(u(j)-u(k))+b_vv*(v(j)-v(k)))
end do
func_u(k)=u(k)+h*((u(k)-(u(k)**3)/3.0-v(k)+sigma/(2.0*p)*effect_u)/epsilon)
func_v(k)=v(k)+h*(u(k)+a(k)+sigma/(2.0*p)*effect_v)
if(t>MaxT/2) then
if(v(k)>0.5.and.func_v(k)<0.5) then
count_number(k)=count_number(k)+1
if(count_number(k)>1) then
t_each(k)=t_each(k)+t*h-t_down(K)
end if
t_down(k)=t*h
end if
end if
end do
u=func_u
v=func_v
if(t==MaxT) then
do i=1,N,1
omega(i)=2.0*PI*((count_number(i)-1)/t_each(i))
write(20,*) i,omega(i)
end do
end if
end do
close(20)
write(*,*) "black over!"
case(2)!红线和灰线
do num=1,10,1
call u0_v0()
call Gaussian(a)
count_number=0
t_up=0.0
t_down=0.0
t_each=0.0
omega=0.0
do t=1,MaxT,1
do k=1,N,1
effect_u=0.0D0
effect_v=0.0D0
do j=1,N,1
effect_u=effect_u+neighbour_matrix(k,j)*(b_uu*(u(j)-u(k))+b_uv*(v(j)-v(k)))
effect_v=effect_v+neighbour_matrix(k,j)*(b_vu*(u(j)-u(k))+b_vv*(v(j)-v(k)))
end do
func_u(k)=u(k)+h*((u(k)-(u(k)**3)/3.0-v(k)+sigma/(2.0*p)*effect_u)/epsilon)
func_v(k)=v(k)+h*(u(k)+a(k)+sigma/(2.0*p)*effect_v)
if(t>MaxT/2) then
if(v(k)>0.5.and.func_v(k)<0.5) then
count_number(k)=count_number(k)+1
if(count_number(k)>1) then
t_each(k)=t_each(k)+t*h-t_down(K)
end if
t_down(k)=t*h
end if
end if
end do
u=func_u
v=func_v
if(t==MaxT) then
do i=1,N,1
omega(i)=2.0*PI*((count_number(i)-1)/t_each(i))
if(omegaMin(i)>=omega(i)) then
omegaMin(i)=omega(i)
end if
if(omegaMax(i)<=omega(i)) then
omegaMax(i)=omega(i)
end if
omega_sum(i)=omega_sum(i)+omega(i)
end do
end if
end do
write(*,*) "运行历程:",num
end do
do i=1,N,1
write(30,*) i,omega_sum(i)/10.0
write(40,*) i,omegaMin(i)
write(40,*) i,omegaMax(i)
end do
close(30)
close(40)
write(*,*) "red and gray over!"
case default
write(*,*) "错误!"
end select
return
end subroutine fnf
!建立网状结构
subroutine neighbour(K)
implicit none
integer :: K !单节点K个邻居
integer :: i,j,number
allocate(neighbour_matrix(N,N))
!初始化网络矩阵
neighbour_matrix=0
do i=1,N-1,1
do j=i+1,N,1
if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end if
end do
end do
return
end subroutine neighbour
!生成正态分布的随机数a(k)
subroutine Gaussian(a)
implicit none
integer :: k
real :: x1,x2,a(N),delte_a,a_mean
delte_a=0.0001
a_mean=0.5
do k=1,N
call random_number(x1)
call random_number(x2)
a(k)=cos(2.0*PI*x2)*sqrt(-2.0*delte_a**2*log(x1))+a_mean
end do
return
end subroutine Gaussian
end module FHN
program main
use FHN
implicit none
integer :: p,status
real :: sigma,r
open(20,file="data_k_omega_black.txt")
open(30,file="data_k_omegaAverage_red.txt")
open(40,file="data_k_omegaMinMax_gray.txt")
call random_seed()
write(*,*) "请输入耦合半径r和耦合强度σ:"
read(*,*) r,sigma
p=nint(r*N)
write(*,*) p,sigma,r
call neighbour(2*p)
do status=1,2,1
call fnf(p,sigma,status)
end do
deallocate(neighbour_matrix)
end program mainfigure 2_A
- r=0.35,sigma=0.1,delte_a=0.0001

figure 2_B
- r=0.35,sigma=0.1,delte_a=0.001
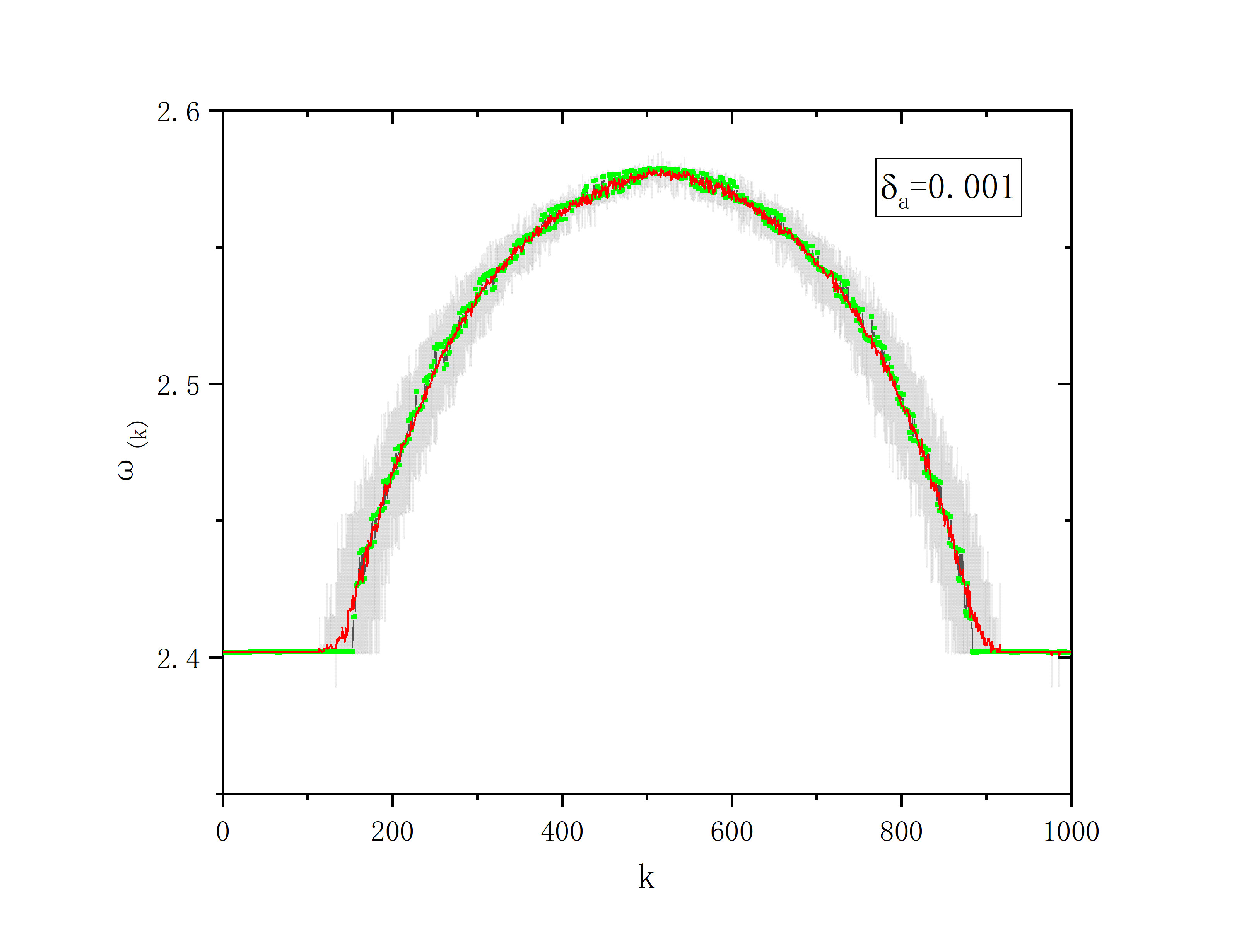
figure 2_C
r=0.35,sigma=0.1,delte_a=0.01
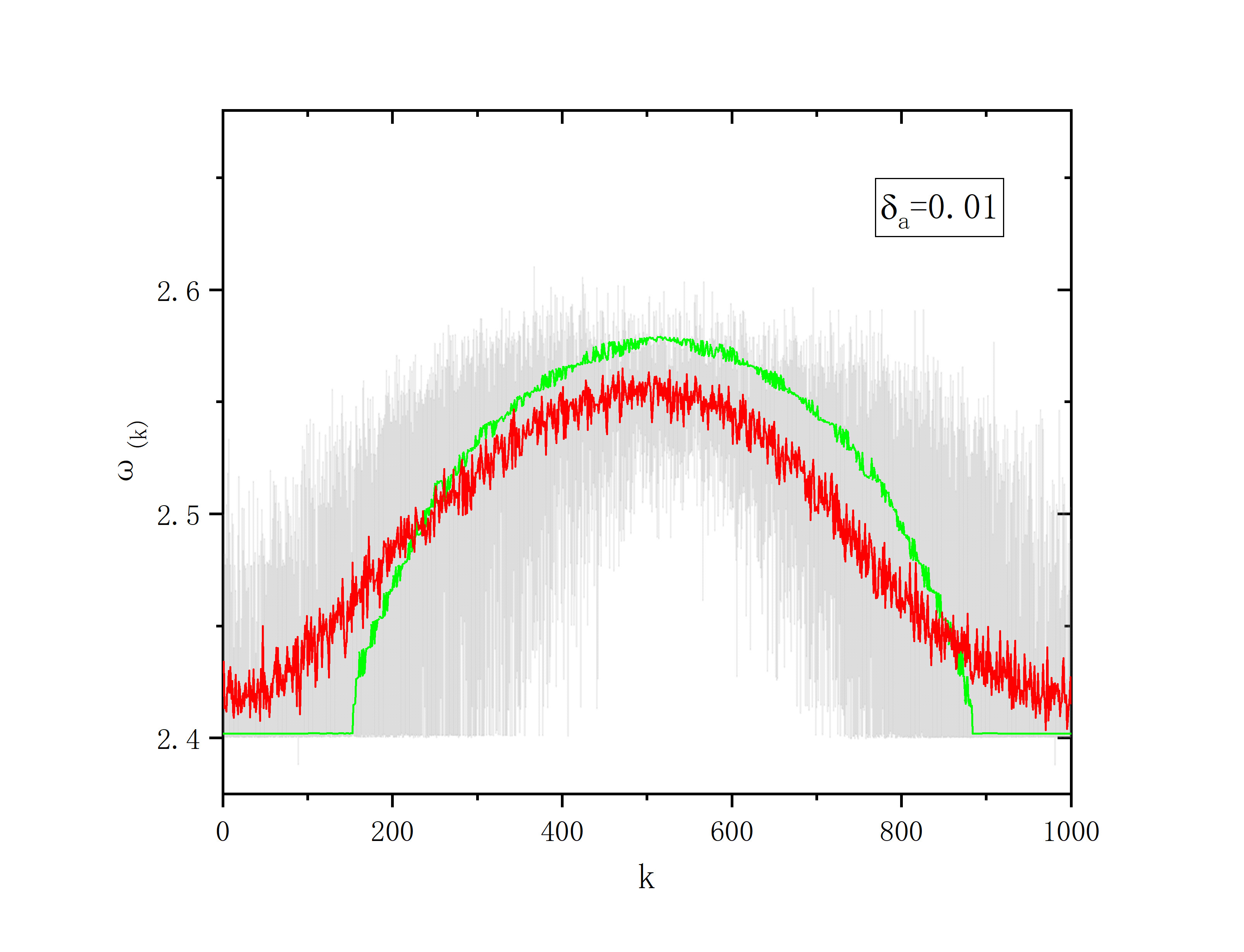
figure 2_D
- r=0.33,sigma=0.28,delte_a=0.0001

figure 2_E
- r=0.33,sigma=0.28,delte_a=0.001

figure 2_F
- r=0.33,sigma=0.28,delte_a=0.01
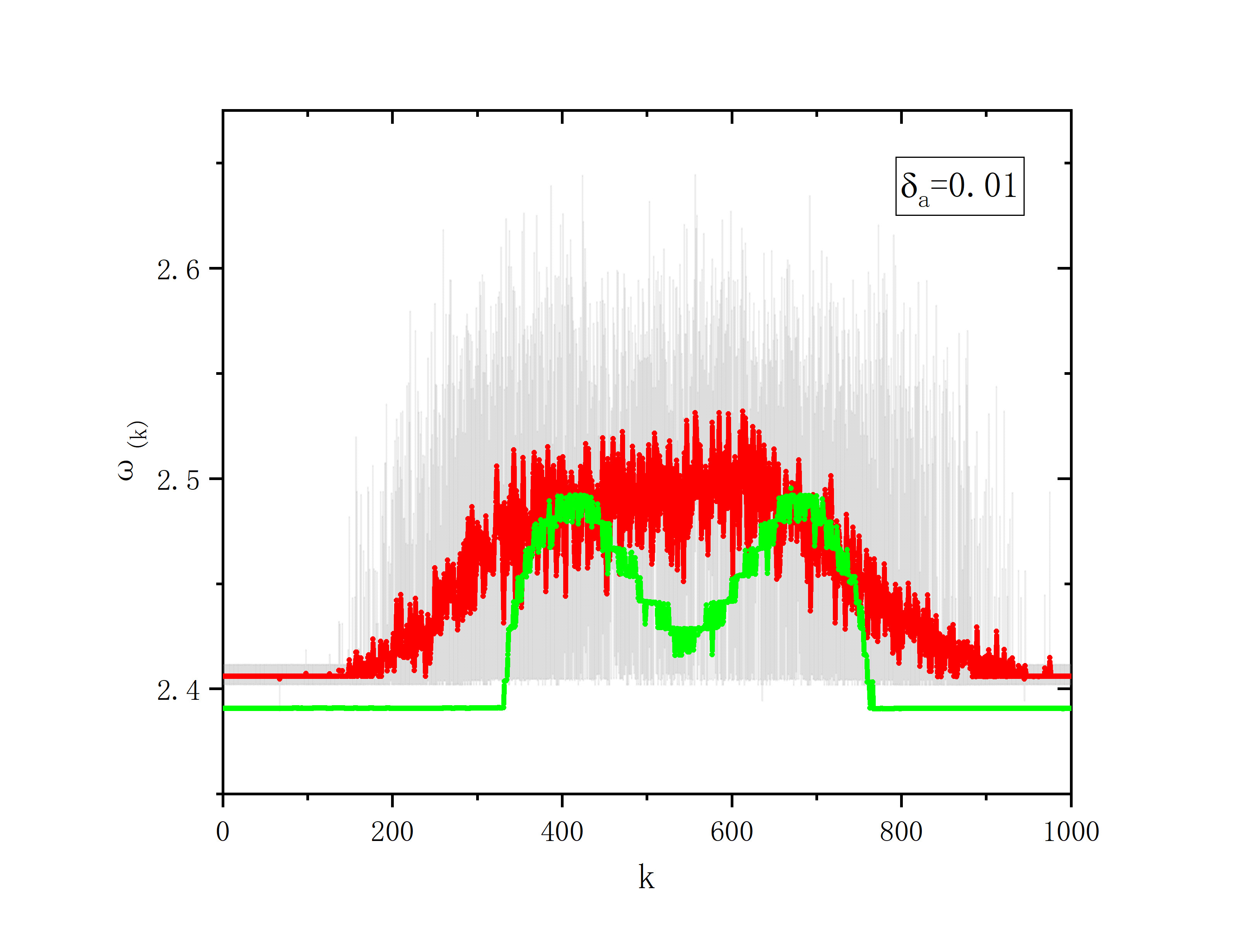
figure 2_G
r=0.25,sigma=0.25,delte_a=0.0001
100次的相速度,t=100000

- 10次,t=50000

figure 2_H
- r=0.25,sigma=0.25,delte_a=0.001
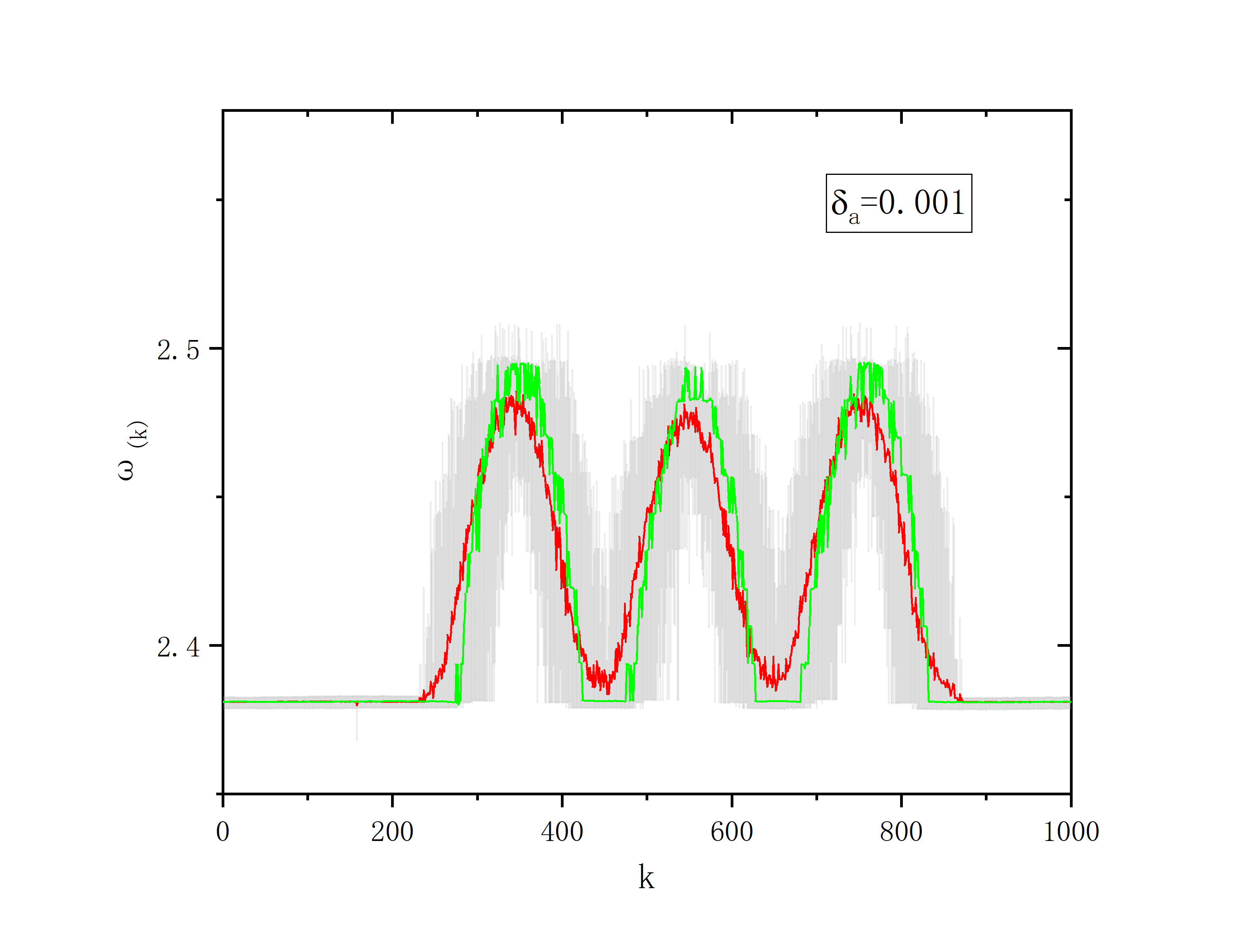
figure 2_I
- r=0.25,sigma=0.25,delte_a=0.01




