探究Lorenz系统下的奇异态

Lorenz系统

单振子

a=10,b=8/3,c=28

module Lorenz
    implicit none
    real,parameter :: h=0.005
    integer,parameter :: N=100,MaxT=130000
    real :: x(N),y(N),z(N)
contains

    subroutine x0_y0_z0()
        implicit none
        integer :: k
        real :: x1,x2,x3
        call random_seed()
        do k=1,N,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(k)=2.0*x1-1.0
            y(k)=2.0*x2-1.0
            z(k)=2.0*x3-1.0
            write(10,*) x(k),y(k),z(k)
        end do
    end subroutine x0_y0_z0

    subroutine fnf()
        implicit none
        integer :: i,j,t
        real :: func_x(N),func_y(N),func_z(N),a,b,c
        a=10.0
        b=8.0/3.0
        c=28.0
        do t=1,MaxT,1
            do i=1,N,1
                func_x(i)=x(i)+h*(a*(y(i)-x(i)))
                func_y(i)=y(i)+h*(c*x(i)-x(i)*z(i)-y(i))
                func_z(i)=z(i)+h*(x(i)*y(i)-b*z(i))
                if(i==1) then
                    write(20,*) x(i),y(i),z(i)
                    write(30,*) t,x(i)
                end if
            end do
            x=func_x
            y=func_y
            z=func_z
        end do
        return
    end subroutine fnf

end module Lorenz



program main
    use Lorenz
    open(10,file="data_x0_y0_z0.txt")
    open(20,file="xyz.txt")
    open(30,file="t_x.txt")
    call x0_y0_z0()
    call fnf()
end program main

• x

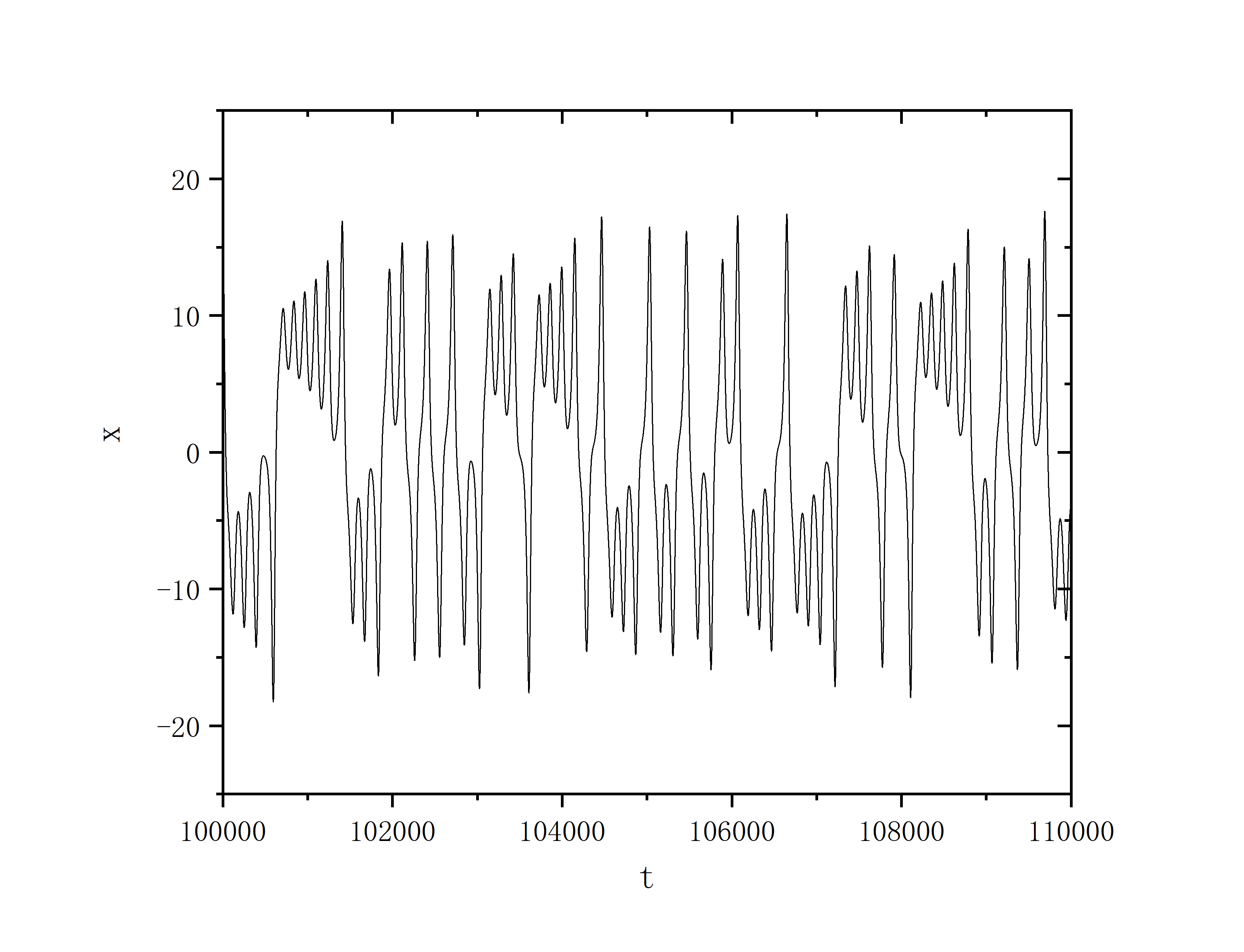
• y

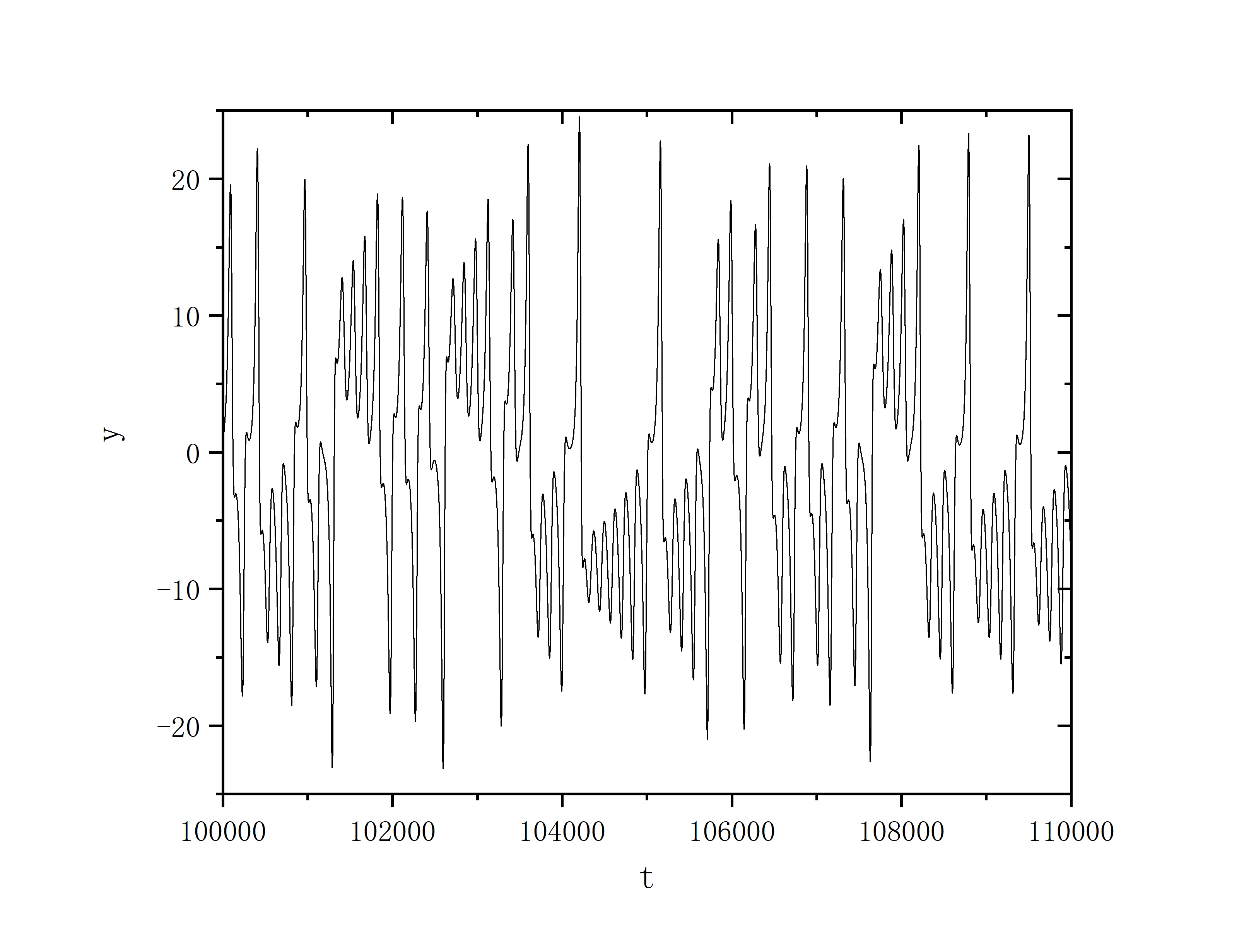
• z

无效分岔图

⚠使用x,y,z来判别是否分岔并不具有有效性，这里的Lorenz的轨迹相对复杂，无法以此作为依据

保持a,b不变，改变c

• 常规求法

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: N=100,MaxT=10000
    real :: x(N),y(N),z(N)
contains

    subroutine x0_y0_z0()
        implicit none
        integer :: k
        real :: x1,x2,x3
        call random_seed()
        do k=1,N,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(k)=2.0*x1-1.0
            y(k)=2.0*x2-1.0
            z(k)=2.0*x3-1.0
            write(10,*) x(k),y(k),z(k)
        end do
        !x=0.1
        !y=0.1
        !z=0.1
    end subroutine x0_y0_z0

    subroutine fnf(c)
        implicit none
        integer :: i,j,t
        real :: func_x(N),func_y(N),func_z(N),a,b,c
        a=10.0
        b=8.0/3.0
        do t=1,MaxT,1
            do i=1,N,1
                func_x(i)=x(i)+h*(a*(y(i)-x(i)))
                func_y(i)=y(i)+h*(c*x(i)-x(i)*z(i)-y(i))
                func_z(i)=z(i)+h*(x(i)*y(i)-b*z(i))
                if(i==1.and.t>9900) then
                    write(20,*) x(i),y(i),z(i)
                    write(30,*) t,x(i)
                    write(40,*) c,x(i)
                end if
            end do
            x=func_x
            y=func_y
            z=func_z
        end do
        return
    end subroutine fnf

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i
    real :: c
    open(10,file="data_x0_y0_z0.txt")
    open(20,file="xyz.txt")
    open(30,file="t_x.txt")
    open(40,file="c_x.txt")
    !c=15.0
    !call x0_y0_z0()
    !call fnf(c)
    do i=0,10000,1
        c=i*0.01
        write(*,*) i
        call x0_y0_z0()
        call fnf(c)
    end do
end program main

• 随机初始条件

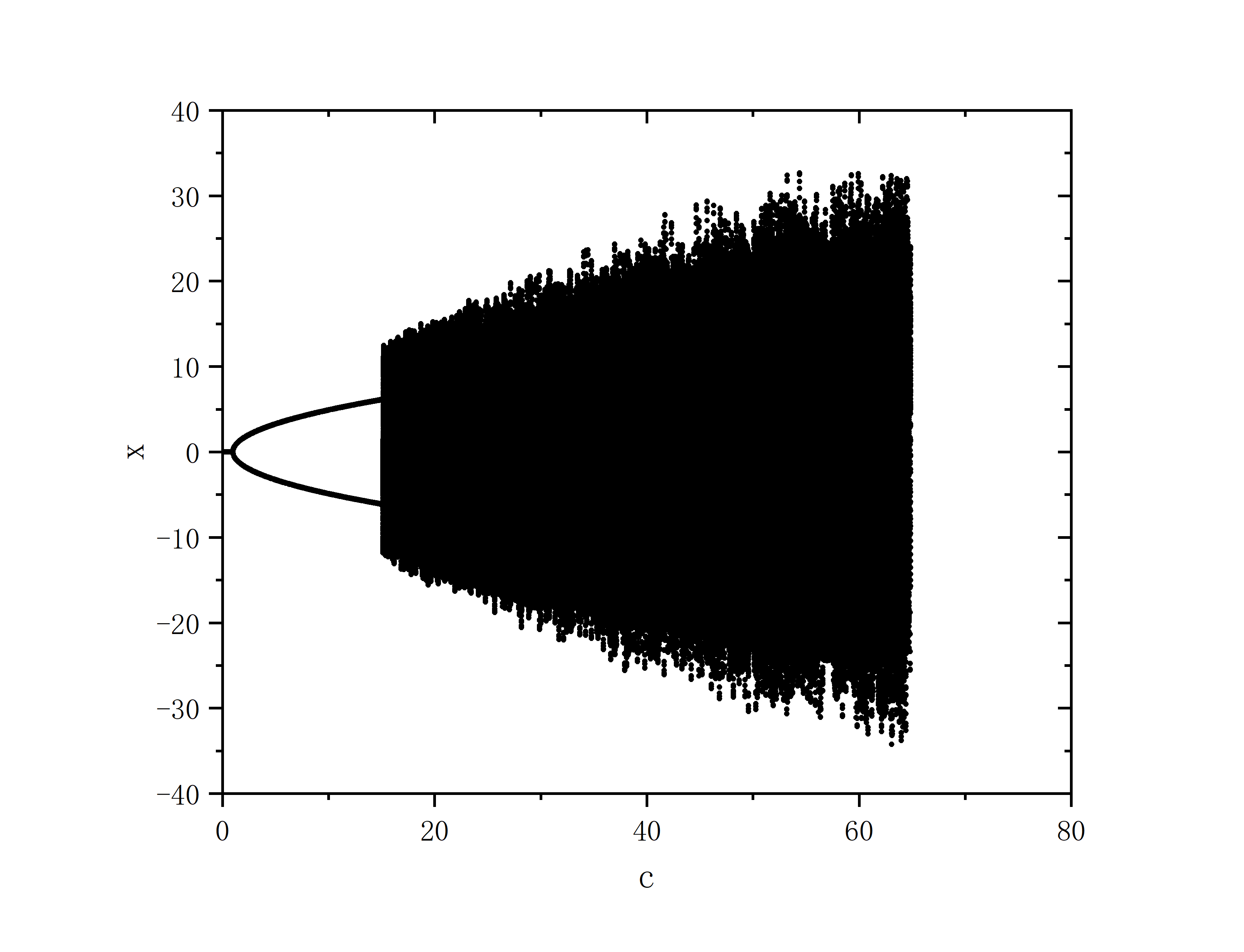
• 固定初值

• 庞加莱截面法

保持a,c不变，改变b

• 随机初始条件

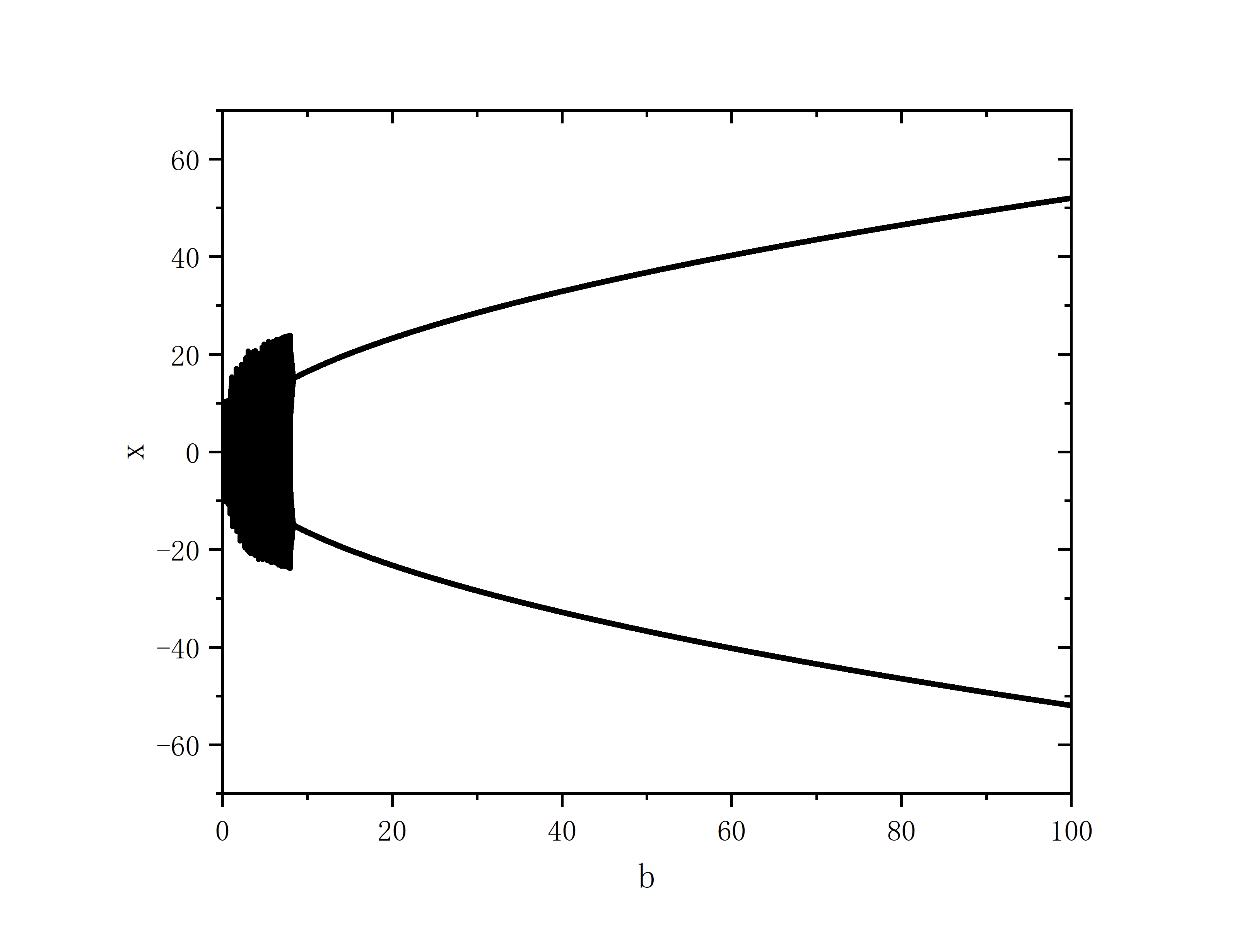
• 固定初值

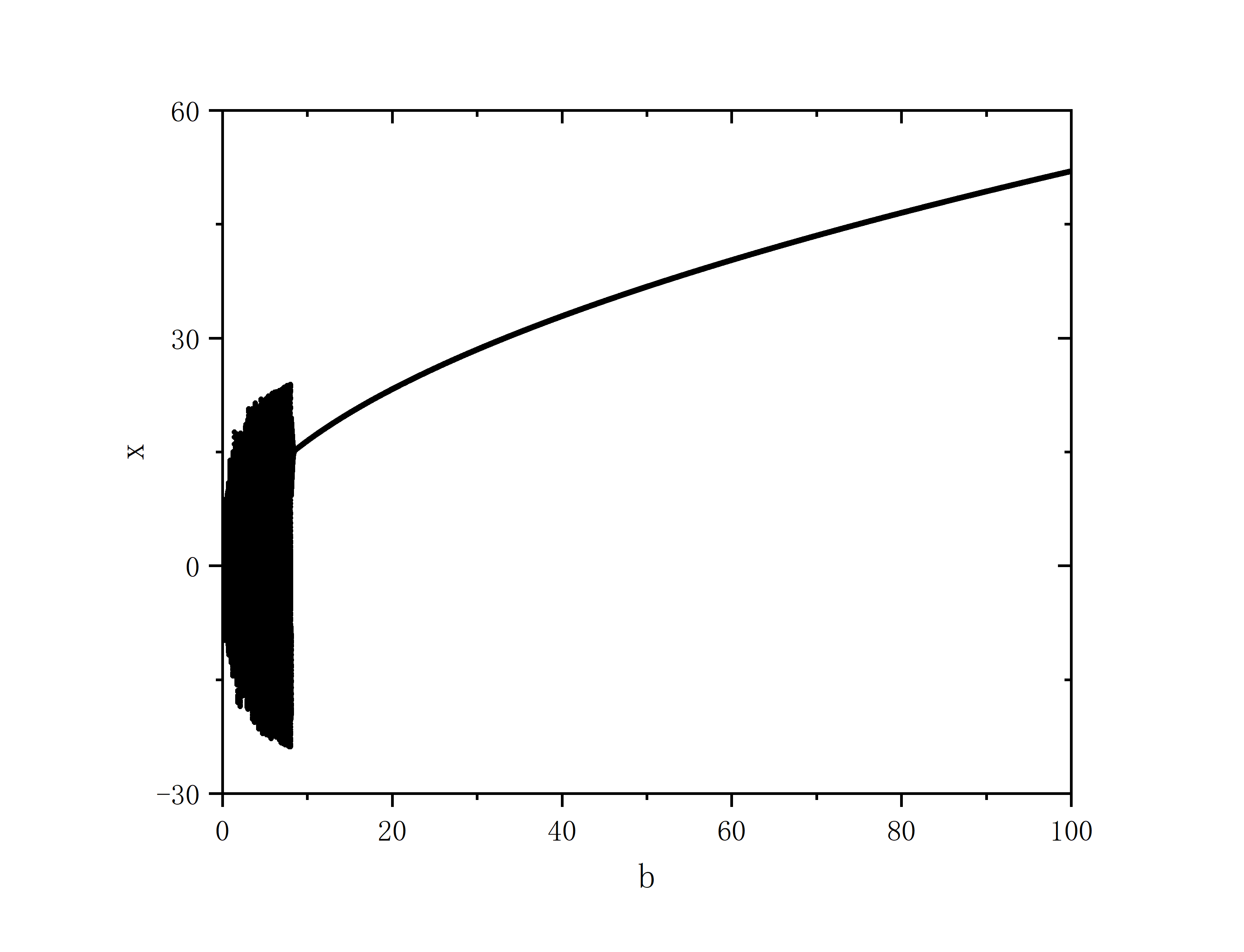
保持b,c不变，改变a

• 随机初始条件

• 固定初值

有效分岔图

• 根据过原点的间隔时间来作为周期分岔依据，即一圈的时间。

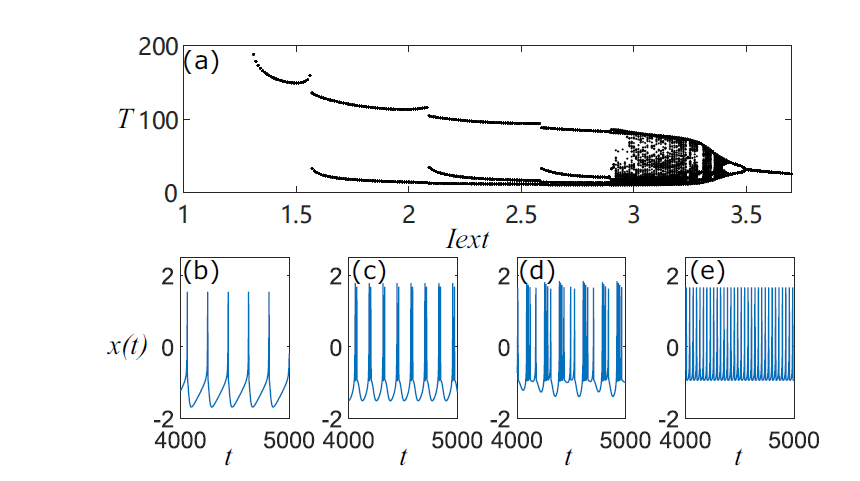
• 例子来源：Remote firing propagation in the neural network of C. elegans

• 以x的时间序列为依据

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=20000
    real :: x,y,z
contains

    subroutine fnf(c)
        implicit none
        integer :: i,j,t,count_up,count_down,status
        real :: func_x,func_y,func_z,a,b,c,T_interval,T_start,T_end
        a=10.0
        b=8.0/3.0
        x=0.001
        y=0.001
        z=0.001
        count_down=0
        count_up=0
        T_start=0.0
        T_end=0.0
        T_interval=0.0
        status=0
        do t=1,MaxT,1
            func_x=x+h*(a*(y-x))
            func_y=y+h*(c*x-x*z-y)
            func_z=z+h*(x*y-b*z)
            x=func_x
            y=func_y
            z=func_z
            if(t>10000) then
                if(x<0.0) then
                    count_down=count_down+1    
                end if
                if(x>0.0.and.abs(T_start-0.0)<0.1) then
                    T_start=t
                end if
                if(x<0.0.and.abs(T_start-0.0)>0.1) then
                    count_up=count_up+1
                end if 
                if(x>0.0.and.count_up>5) then
                    T_end=t
                    T_interval=T_end-T_start
                    write(30,*) T_interval
                    status=status+1
                    if(status>1) then
                        write(40,*) c,T_interval*h
                    end if    
                    count_up=0
                    count_down=0
                    T_start=0.0
                end if    
                write(20,*) t,x
            end if
        end do
        return
    end subroutine fnf

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i
    real :: c
    open(10,file="data_x0_y0_z0.txt")
    open(20,file="c_x.txt")
    open(30,file="T_interval.txt")
    open(40,file="c_T_interval.txt")
    do i=0,10000,1
        c=i*0.01
        write(*,*) i
        call fnf(c)
    end do
    close(10)
    close(20)
    close(30)
    close(40)
end program main

a_T

b_T

c_T

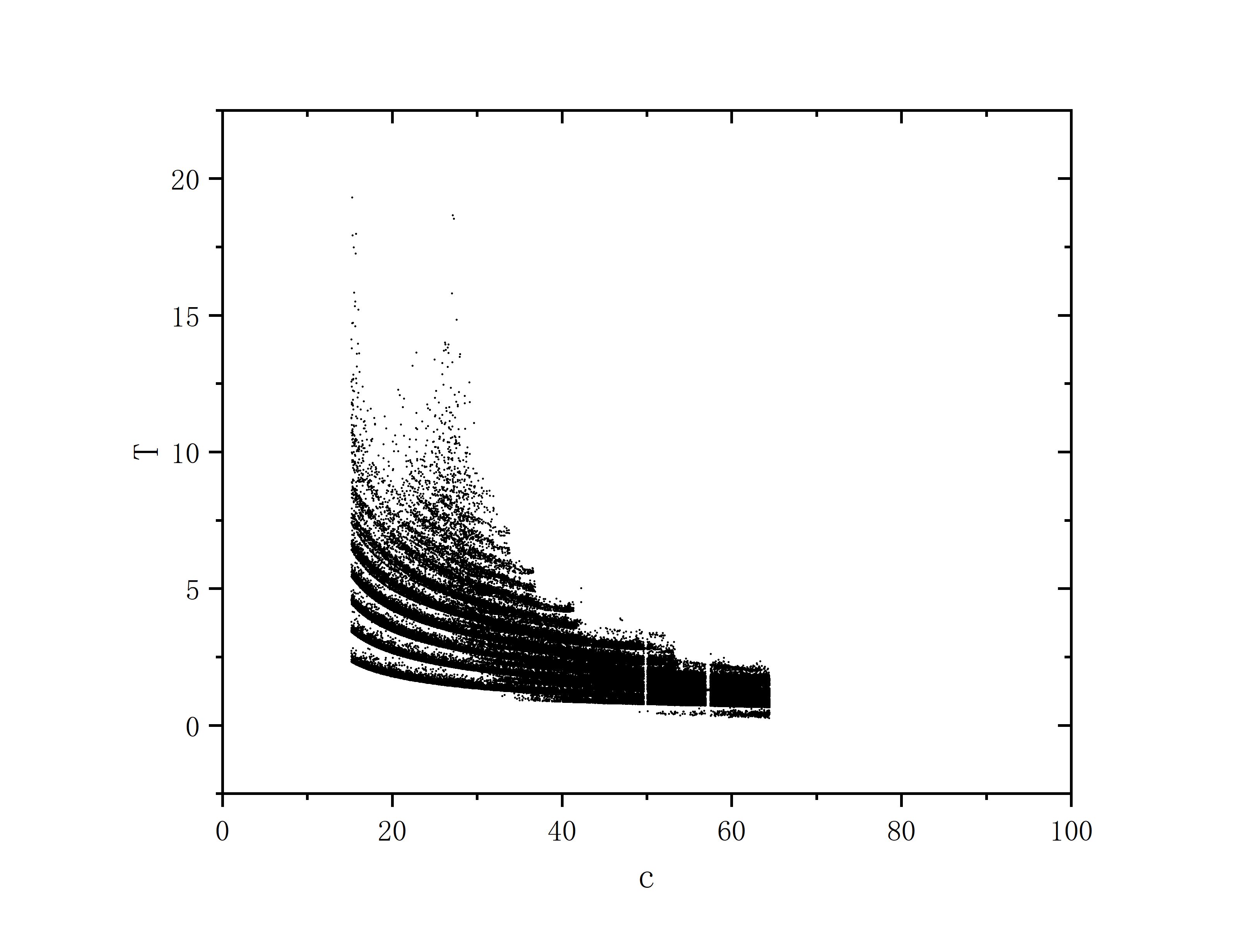
a=10,b=8.0/3.0,c=28.0

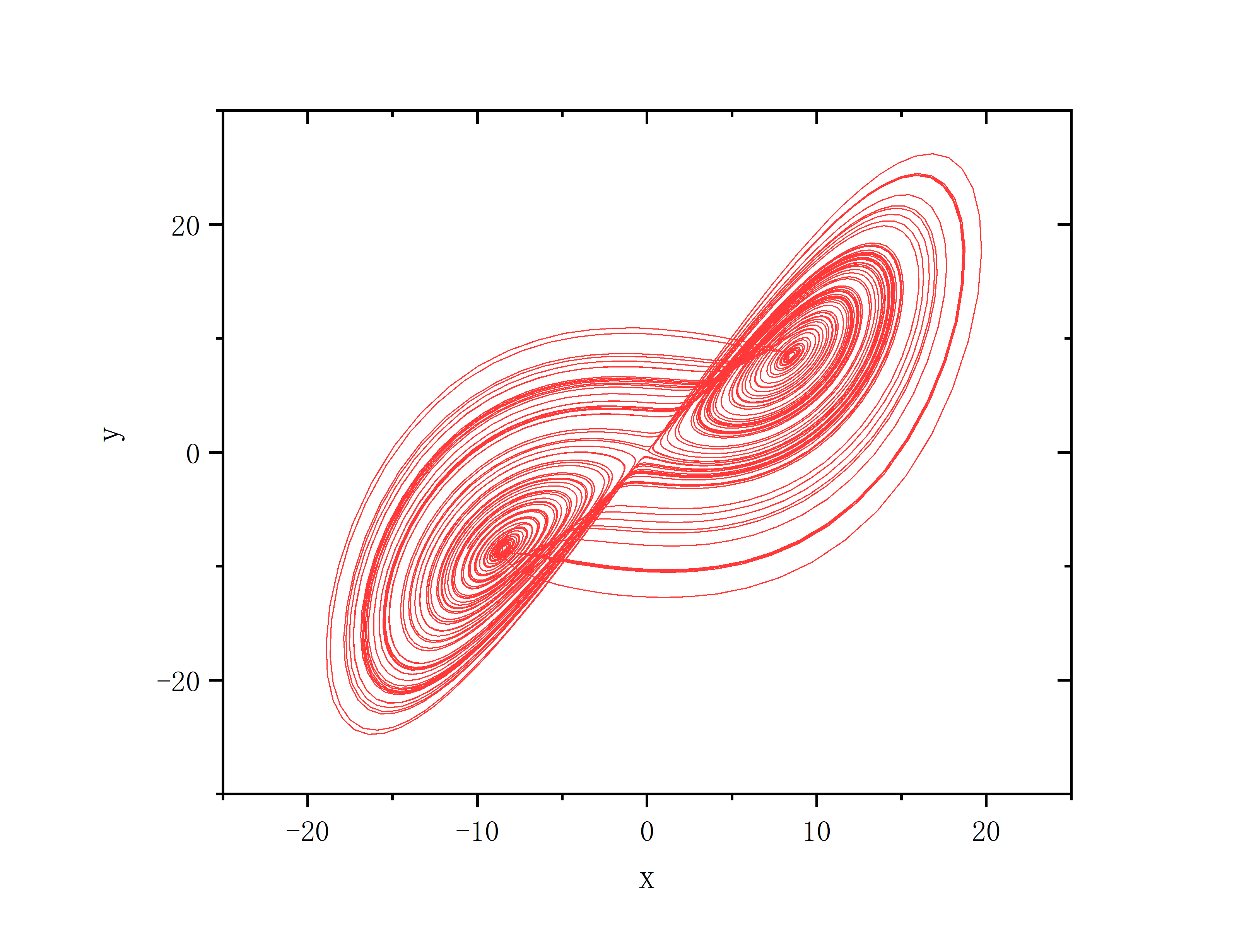
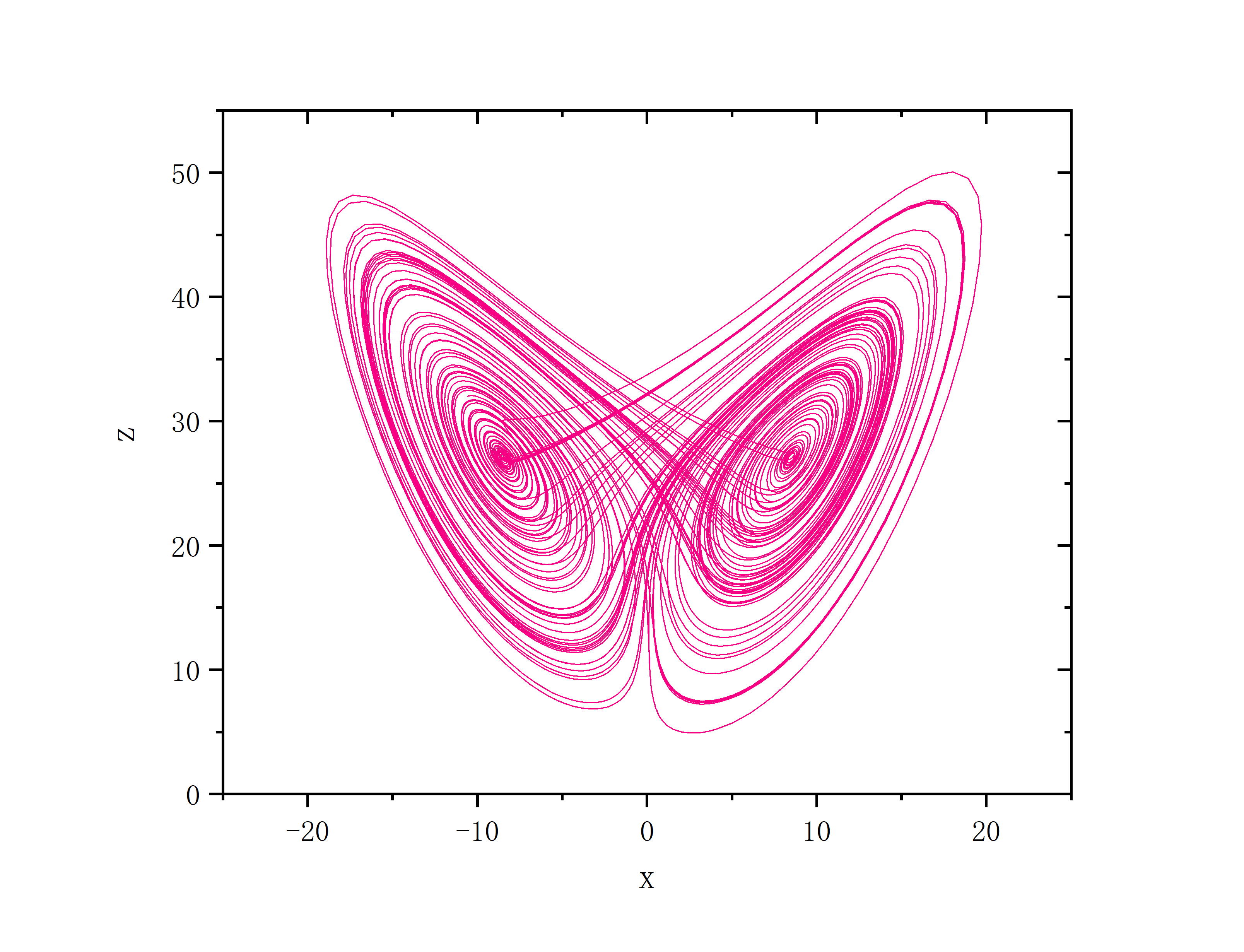
a=40,b=8.0/3.0,c=28.0

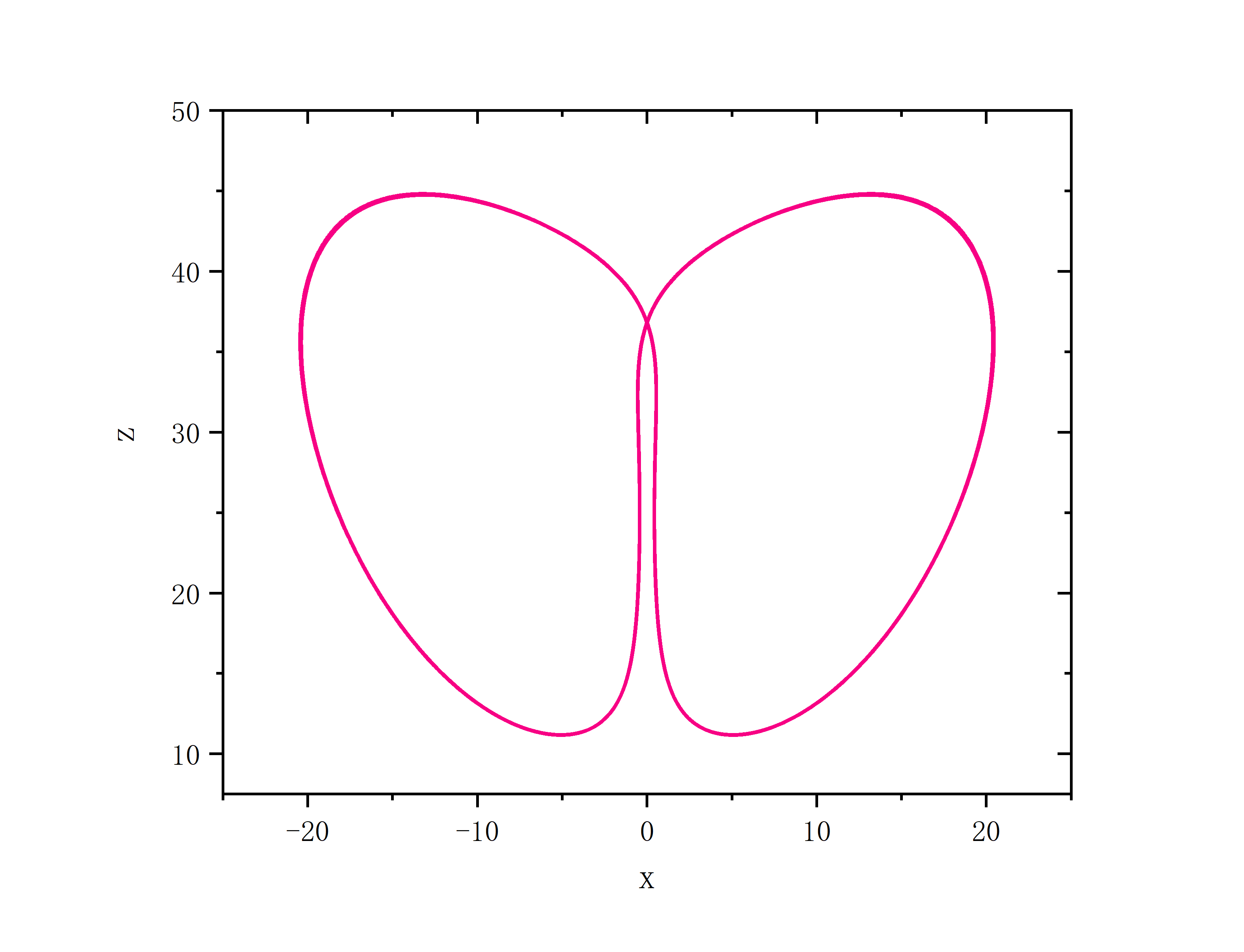
a=10,b=0.54,c=28.0

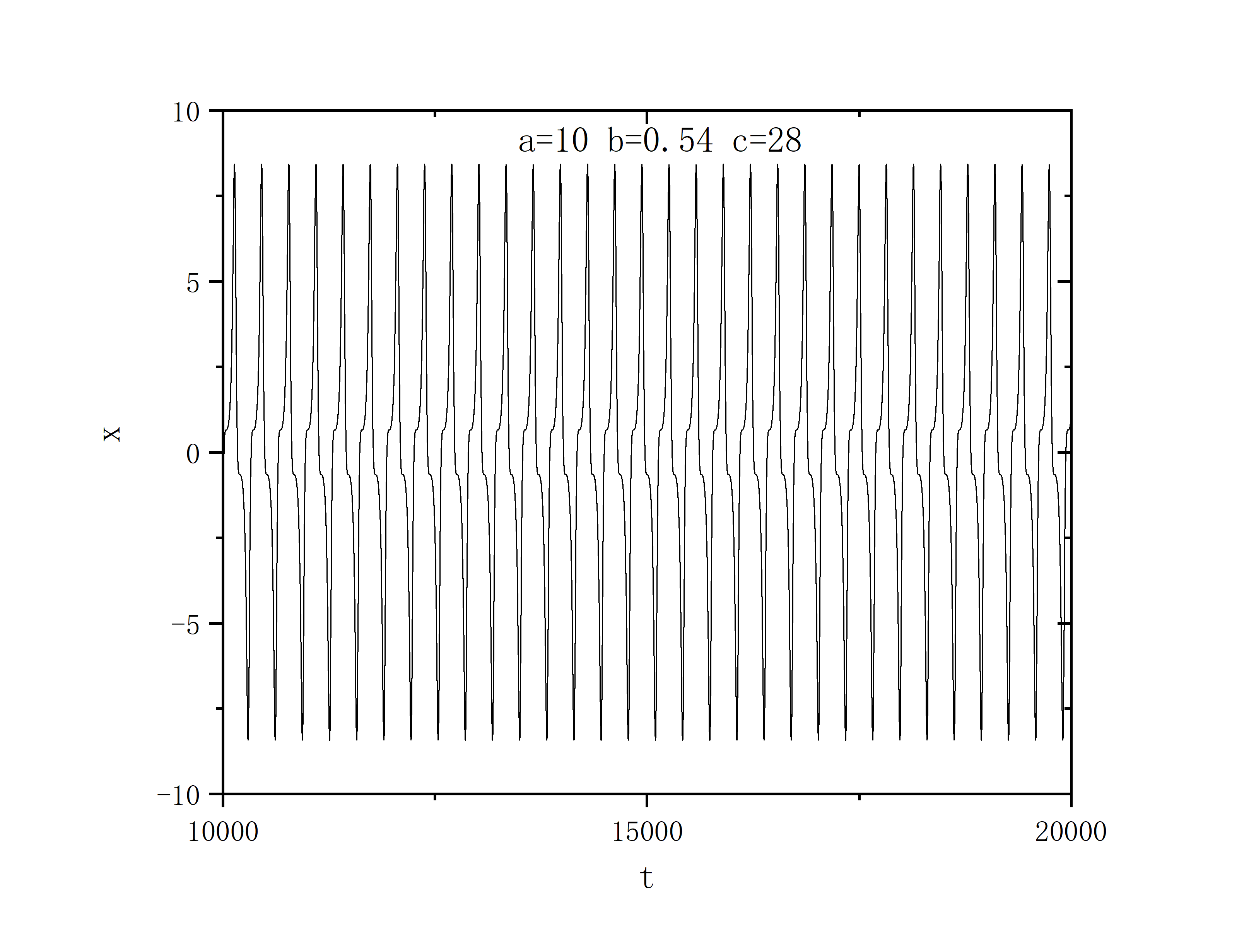
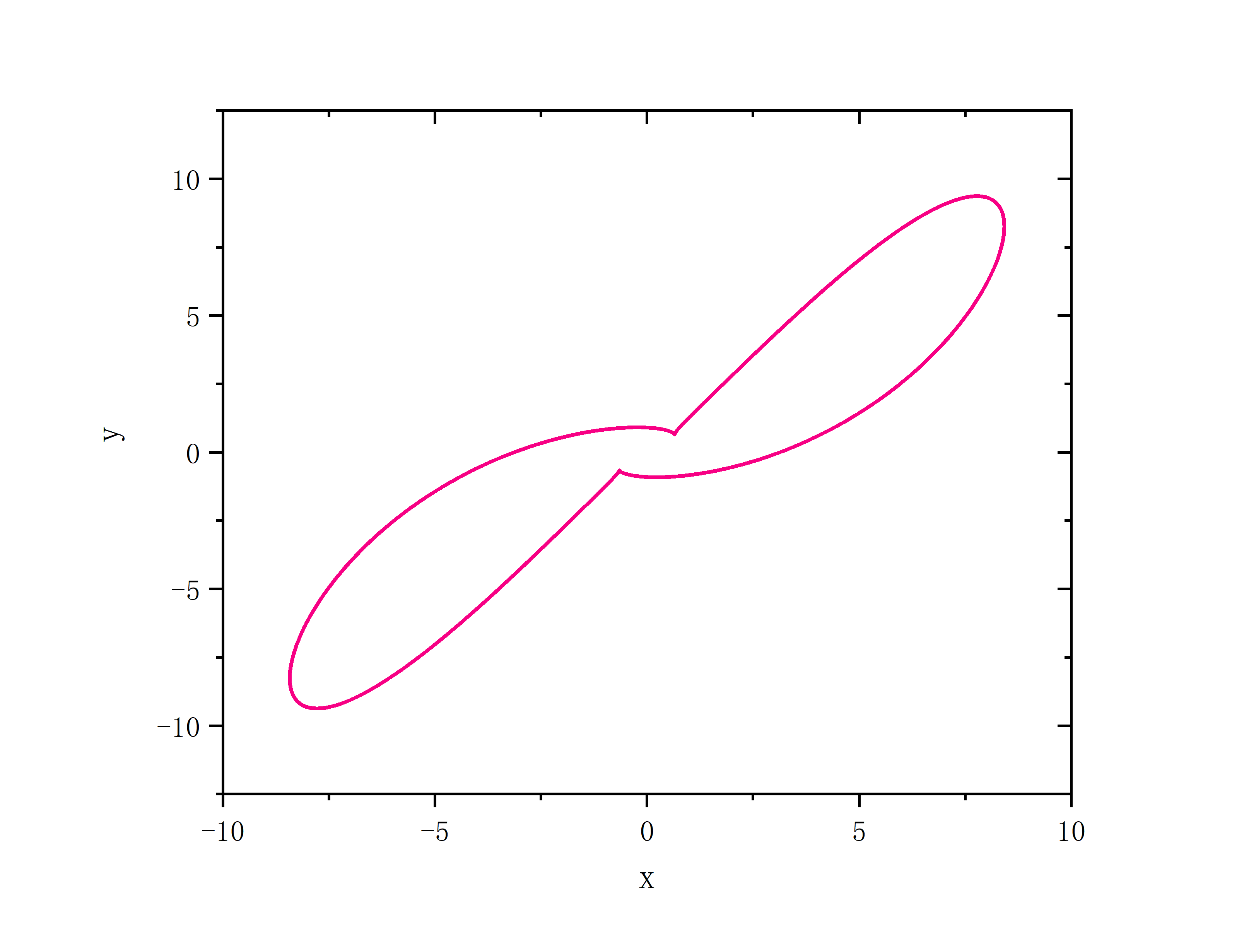
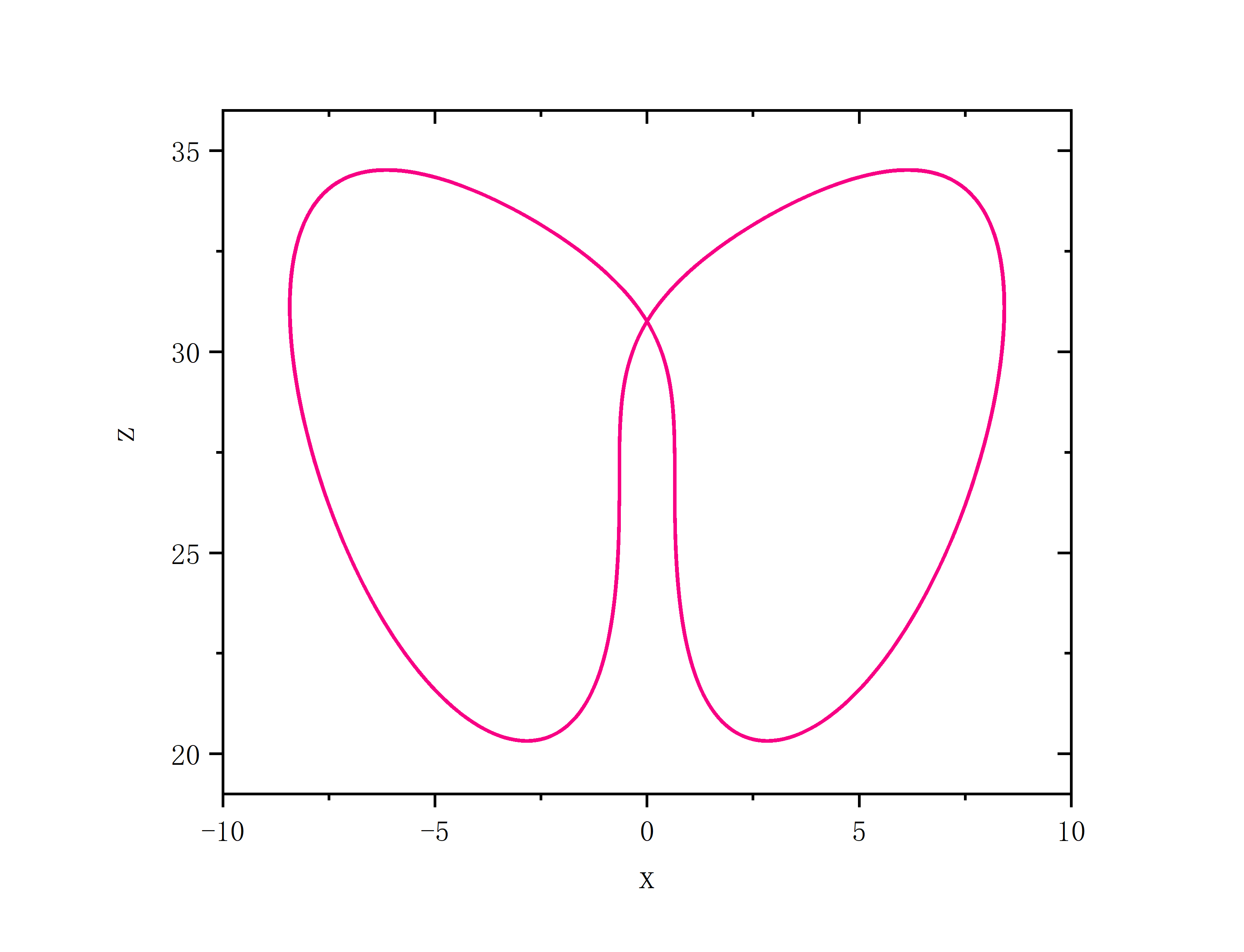
a=10,b=8.0/3.0,c=50

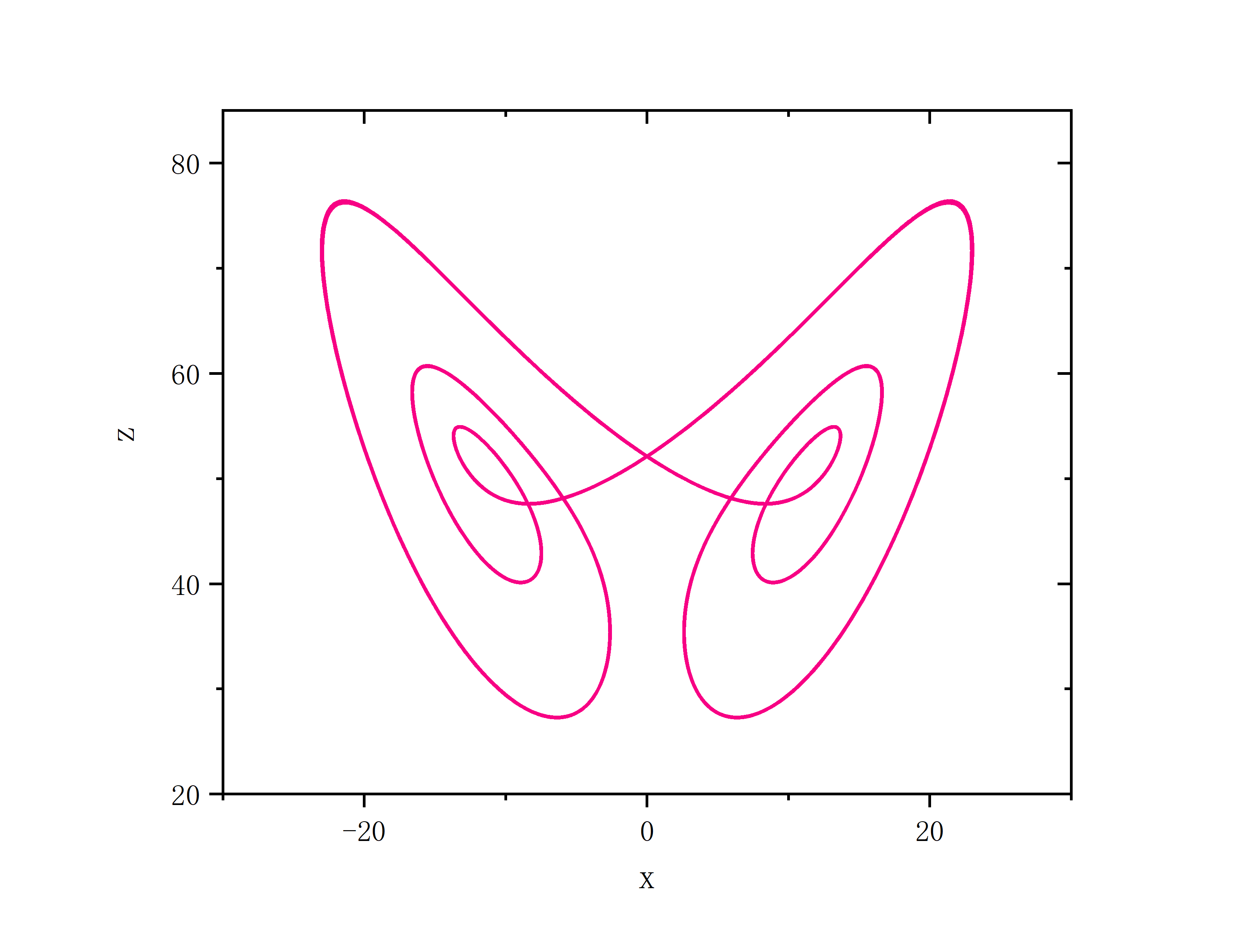
a=10,b=8.0/3.0,c=57.3

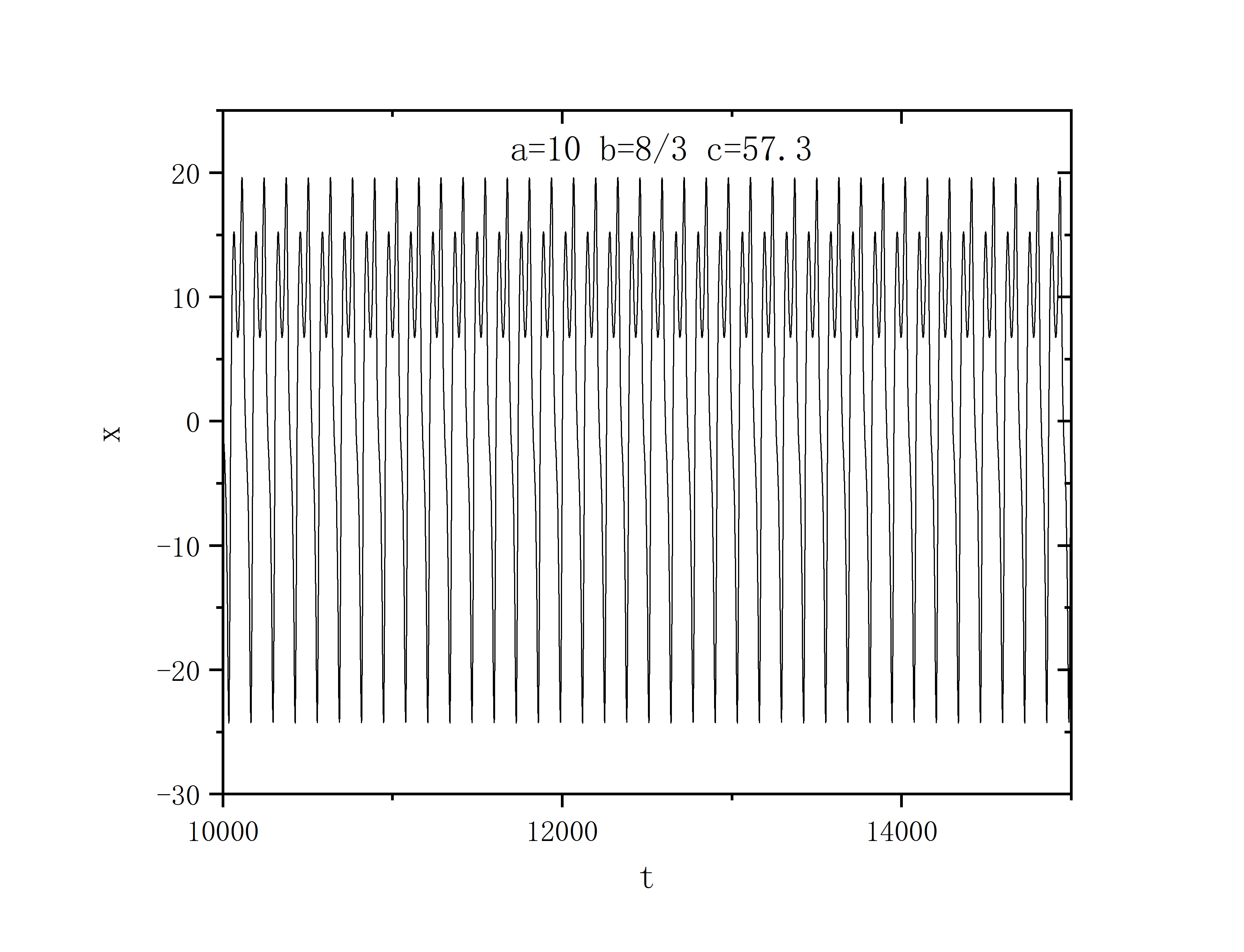
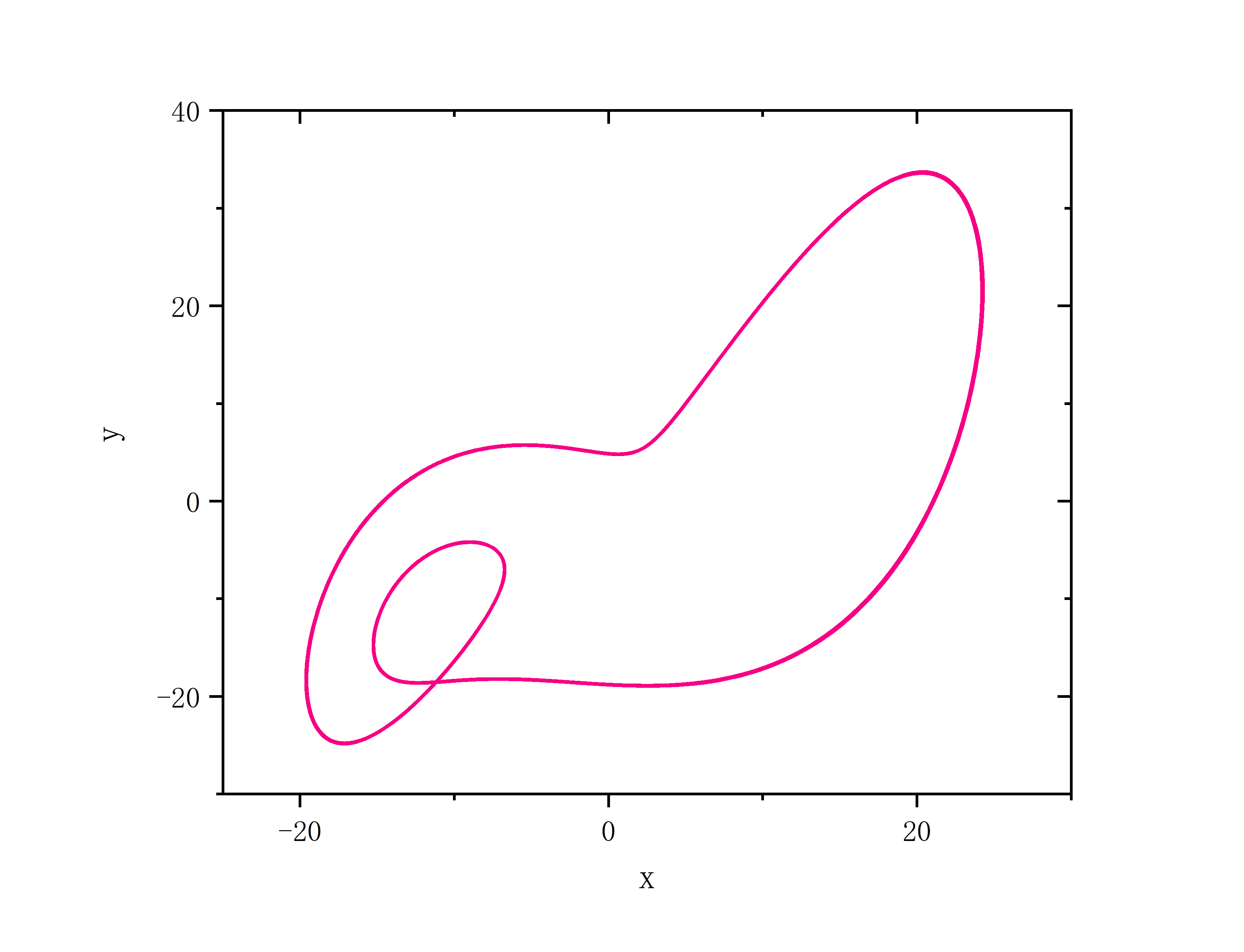
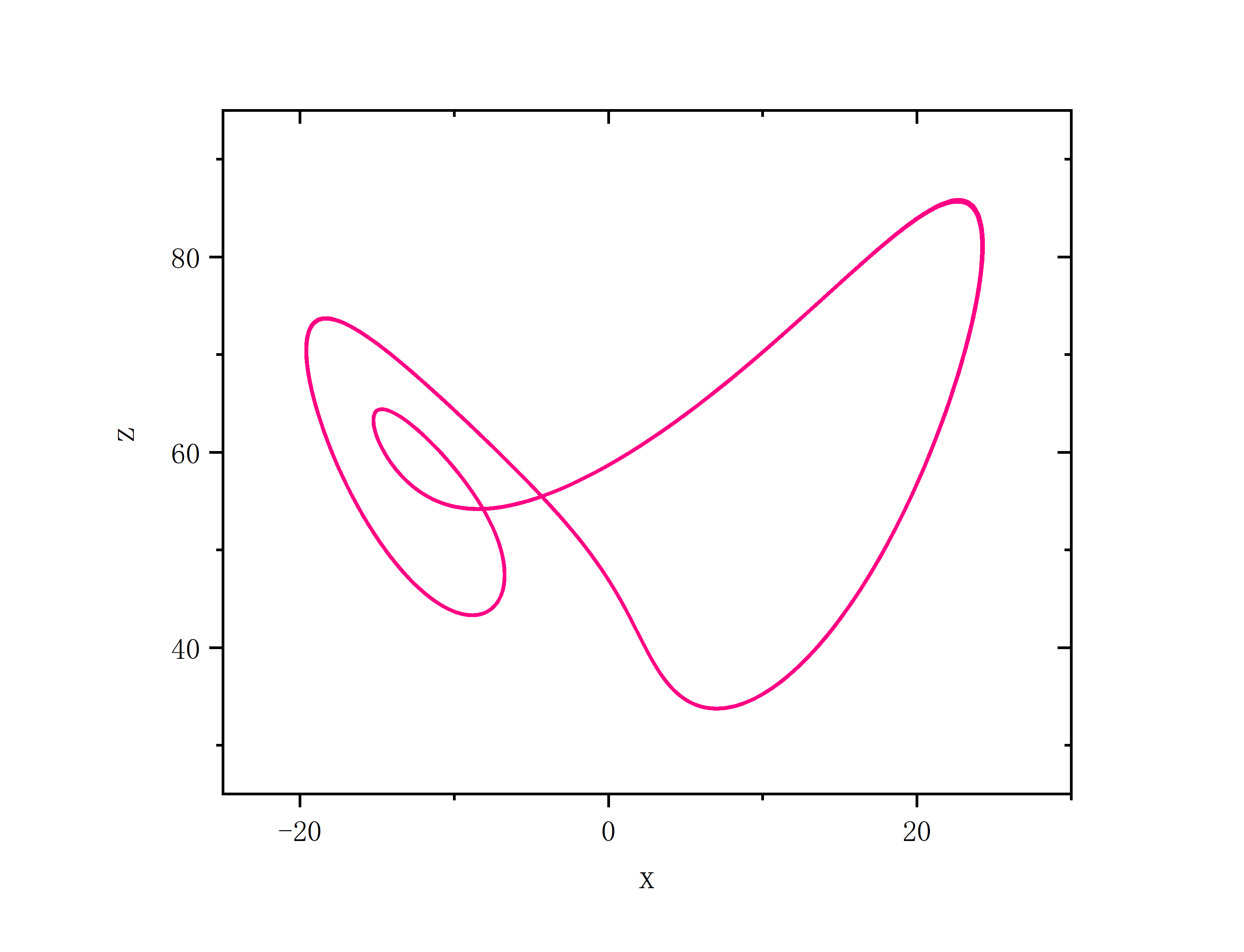
频率奇异态

module Rossler
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: N=100,MaxT=130000
    integer,allocatable :: neighbour_matrix(:,:)
    real :: x(N),y(N),z(N)
contains

    subroutine x0_y0_z0()
        implicit none
        integer :: k
        real :: x1,x2,x3
        call random_seed()
        do k=1,N,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(k)=2.0*x1-1.0
            y(k)=2.0*x2-1.0
            z(k)=2.0*x3-1.0
            !x(k)=x1
            !y(k)=x2
            !z(k)=x3
            write(10,*) x(k),y(k),z(k)
        end do
        !x=0.001
        !y=0.001
        !z=0.001
    end subroutine x0_y0_z0

    subroutine fnf(p)
        implicit none
        integer :: i,j,p,t
        real :: func_x(N),func_y(N),func_z(N),a,b,c,tau(N),epsilon,coupling(N),random,x_change(N,MaxT),&
                &count_number_up(N),count_number_down(N),t_start(N),t_end(N),t_change(N),f_i(N),count(N)
        a=40.0
        b=8.0/3.0
        c=28.0
        tau=1.0
        epsilon=0.6
        count=0.0
        t_change=0.0
        x_change=0.0
!        do i=1,N/2,1
!100         call random_number(random)
!            if(abs(1.0-tau(ceiling(100.0*random)))<0.1) then
!                tau(ceiling(100.0*random))=0.76
!            else
!                goto 100
!            end if
!        end do
        do i=N/2+1,N,1
            tau(i)=0.6
        end do
        write(90,*) tau
        do t=1,MaxT,1
            coupling=0.0
            do i=1,N,1
                do j=1,N,1
                    coupling(i)=coupling(i)+neighbour_matrix(i,j)*(x(j)-x(i))
                end do
                func_x(i)=x(i)+h*(a*(y(i)-x(i))+tau(i)*epsilon*coupling(i))
                func_y(i)=y(i)+h*(c*x(i)-x(i)*z(i)-y(i))
                func_z(i)=z(i)+h*(x(i)*y(i)-b*z(i))
                if(i==25.and.t*h>1000) then
                    write(20,*) t*h,x(i)
                end if
                if(i==41.and.t*h>1000) then
                    write(41,*) t*h,x(i)
                end if
                if(i==60.and.t*h>1000) then
                    write(60,*) t*h,x(i)
                end if
                if(t*h==1000) then
                    write(50,*) i,x(i)
                end if
                if(t>129000) then
                    write(70,*) i,t,x(i)
                end if
                if(t*h>1000) then
                    x_change(i,t)=x(i)
                    if(x_change(i,t)>0.0) then
                        count_number_up(i)=count_number_up(i)+1
                        if(count_number_up(i)==1) then
                            t_start(i)=t*h
                        end if
                    else if(x_change(i,t)<0.0) then
                        count_number_down(i)=count_number_down(i)+1
                    end if
                    if(count_number_up(i)>30.and.count_number_down(i)>30.and.x_change(i,t)>0.0) then
                        t_end(i)=t*h
                        count(i)=count(i)+1
                        t_change(i)=t_change(i)+1.0/(t_end(i)-t_start(i))
                        count_number_up(i)=0
                        count_number_down(i)=0
                    end if   
                end if
            end do
            x=func_x
            y=func_y
            z=func_z
        end do
        do i=1,N,1
            f_i(i)=(1.0/(count(i)+1))*t_change(i)
            write(80,*) i,f_i(i)
        end do
        return
    end subroutine fnf
    !建立网状结构

    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(N,N))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,N-1,1
            do j=i+1,N,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=N-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,N,1
            do j=1,N,1
                write(30,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(30,*)
        end do
        return
    end subroutine neighbour

end module Rossler



program main
    use Rossler
    implicit none
    integer :: p
    p=1
    open(10,file="data_x0_y0_z0.txt")
    open(20,file="data_i_20.txt")
    open(41,file="data_i_45.txt")
    open(60,file="data_i_70.txt")
    open(50,file="data_i_x.txt")
    open(30,file="neighbour_matrix.txt")
    open(70,file="i_t_x.txt")
    open(80,file="i_fi.txt")
    open(90,file="tau.txt")
    call x0_y0_z0()
    call neighbour(2*p)
    call fnf(p)
    deallocate(neighbour_matrix)
    close(10)
    close(20)
    close(41)
    close(60)
    close(50)
    close(30)
    close(70)
    close(80)
end program main