基于MatCont分析非线性动力学
- MatCont是一个基于Matlab而开发的免费工具包,专门用来做非线性动力学模型分叉、向量场、周期性等分析,符号(连续性)运算和数值(离散性)运算均适用。
使用教程
- 下载MatCont工具包https://sourceforge.net/projects/matcont/
- 解压文件放在matlab安装的toolbox目录
- 运行init.m,安装MatCont
- 启动MatCont,运行MatCont.m文件
案例分析
Pitchfork Bifurcation

- select→system→new
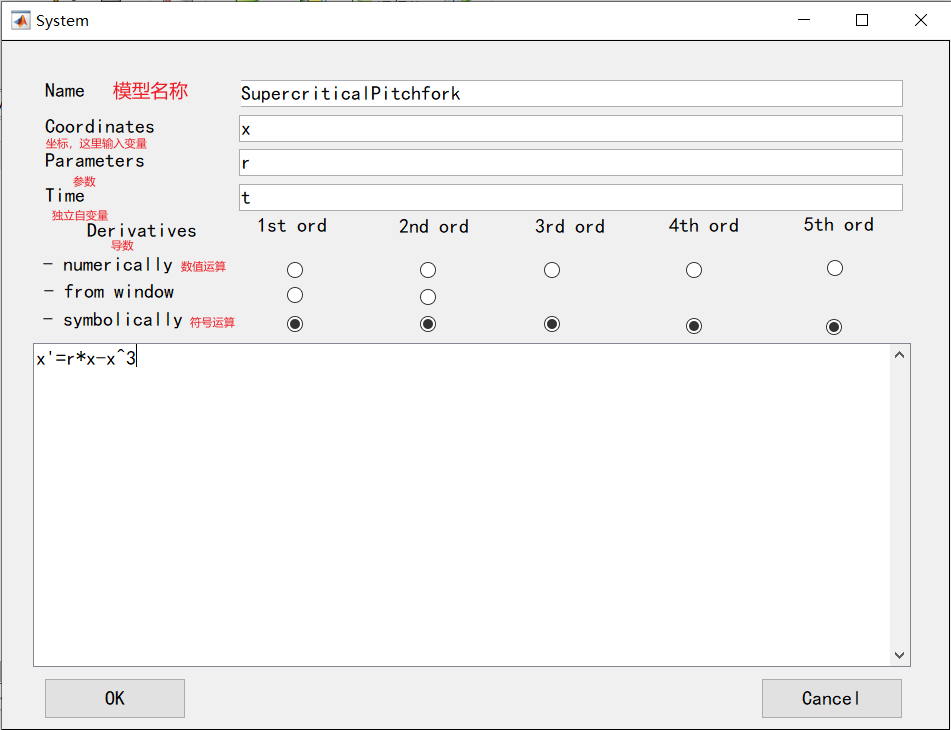
- 符号运算一般是连续性的解析解,数学上优于离散的数值解。解析解求解困难,很多情况无法求解。
- 开始计算,创建初始点Type→Initial Point→Point


- 打开监视窗口,曲线图

- 打开监视窗口,数值显示

- 运行,即结果
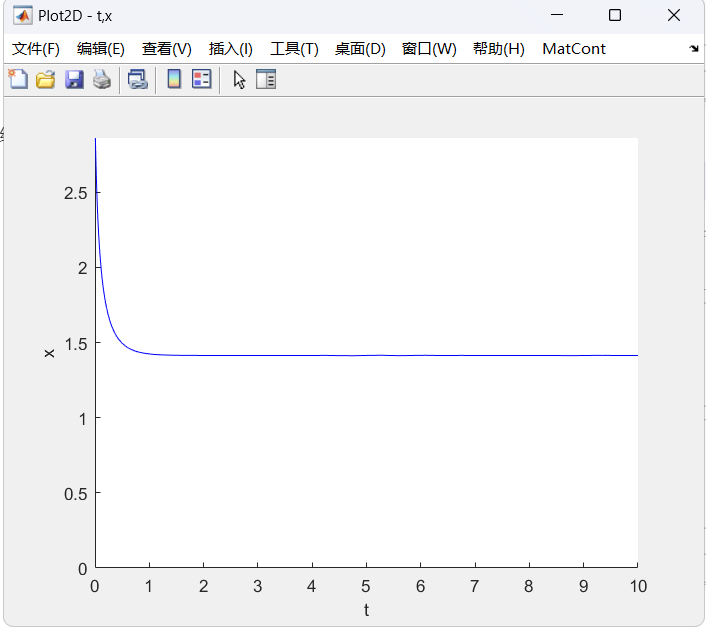

- 画分岔图
- 设置数值显示界面,判断是否稳定

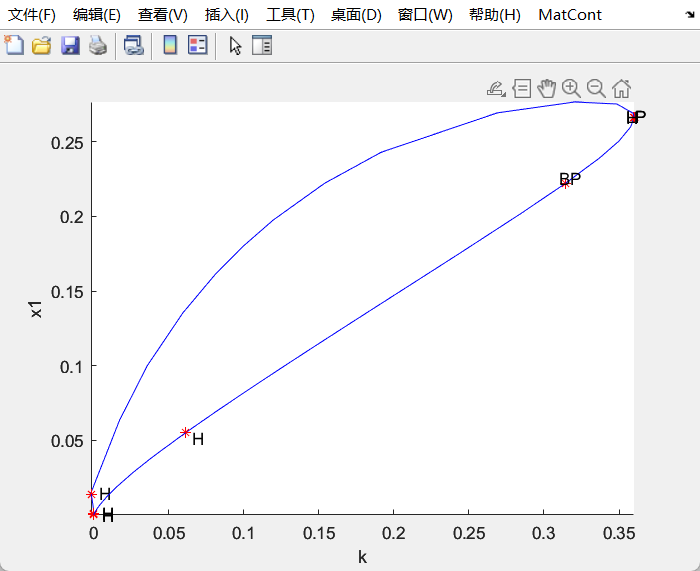
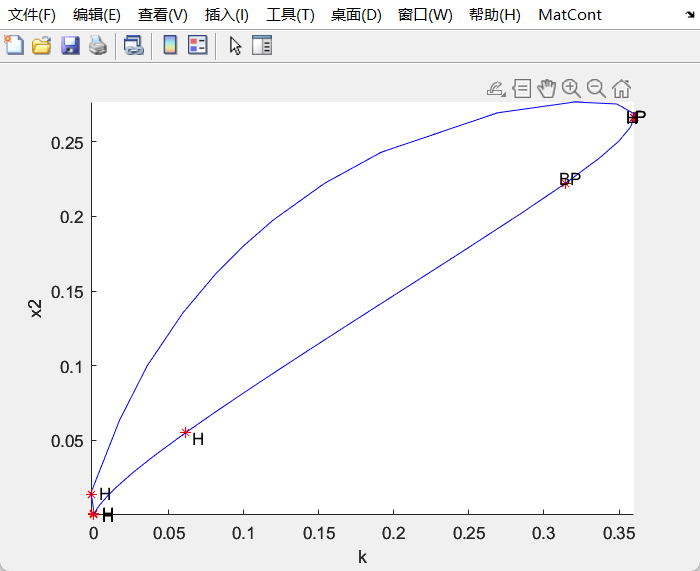
- 画完一个解后,选择另一个解,画其分岔图,首先点击View Result然后双击分叉点Branch point

- 结果
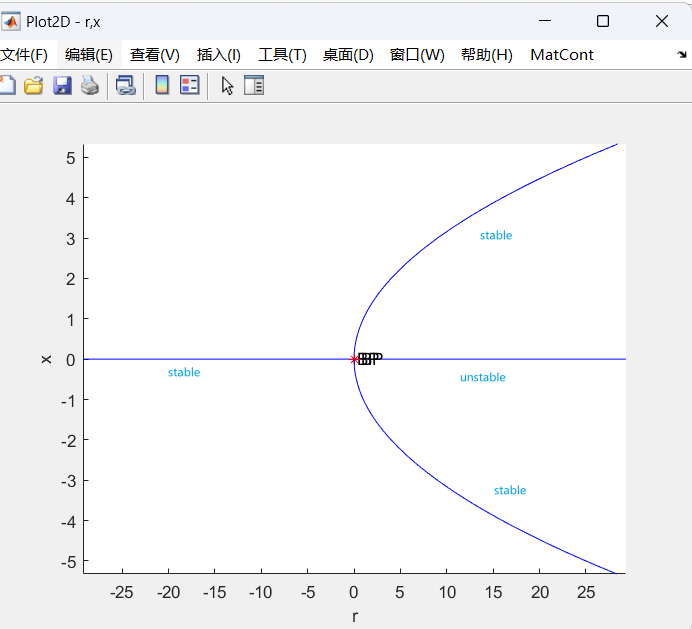
- 导出数据重新画图

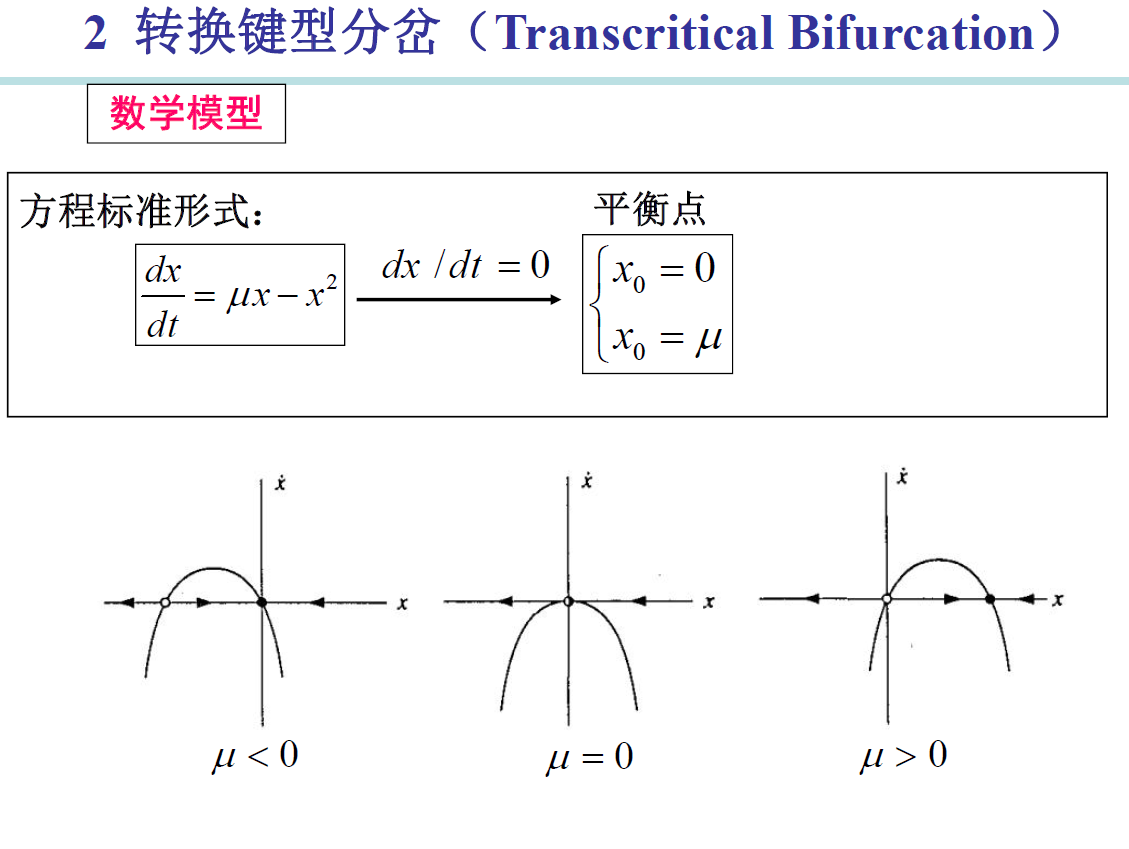
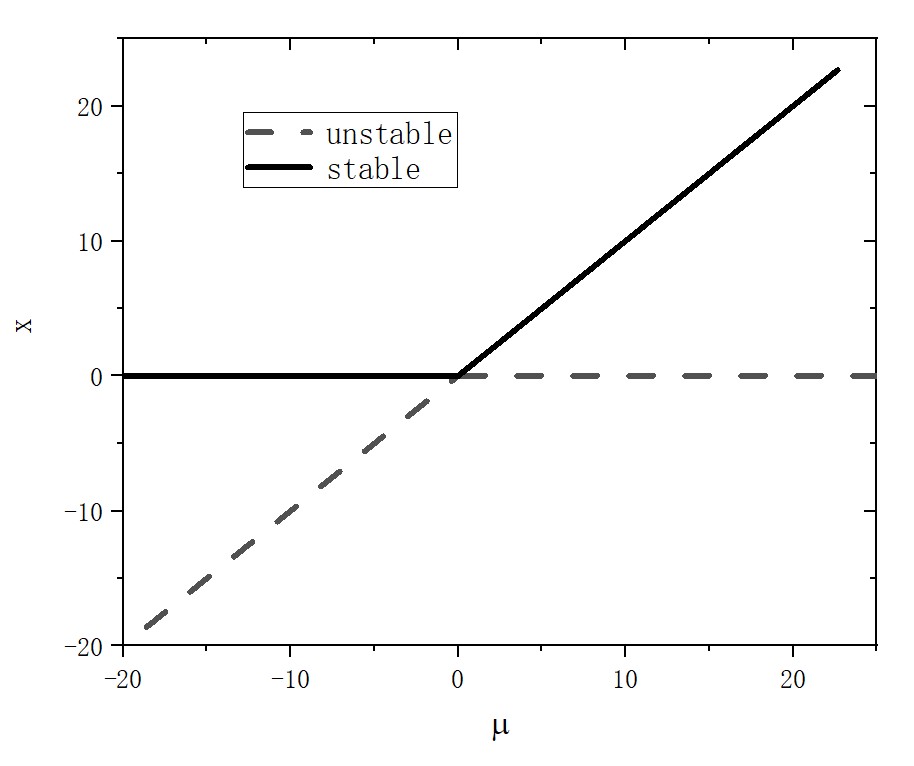
Transcritical Bifurcation
The Duffing Equation





- 初值

- 1s
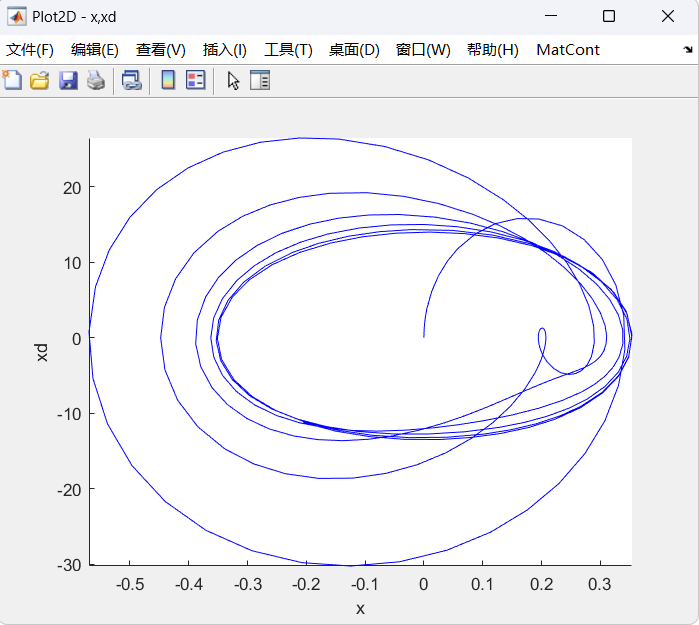
- 清除1s,画第2s,出现极限环
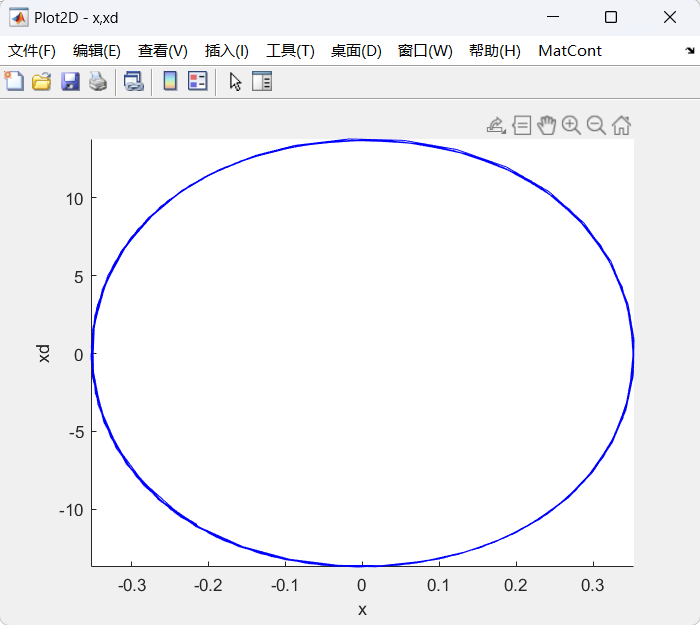
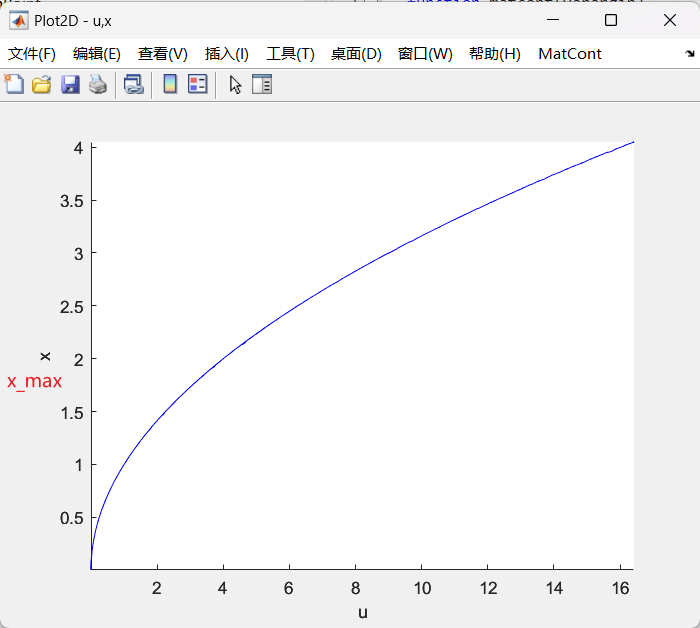
- 选定极限环位置,计算x_max随着w的变换,看极限环是否稳定


- 继续增大w,出现不稳定解


Hopf Bifurcation
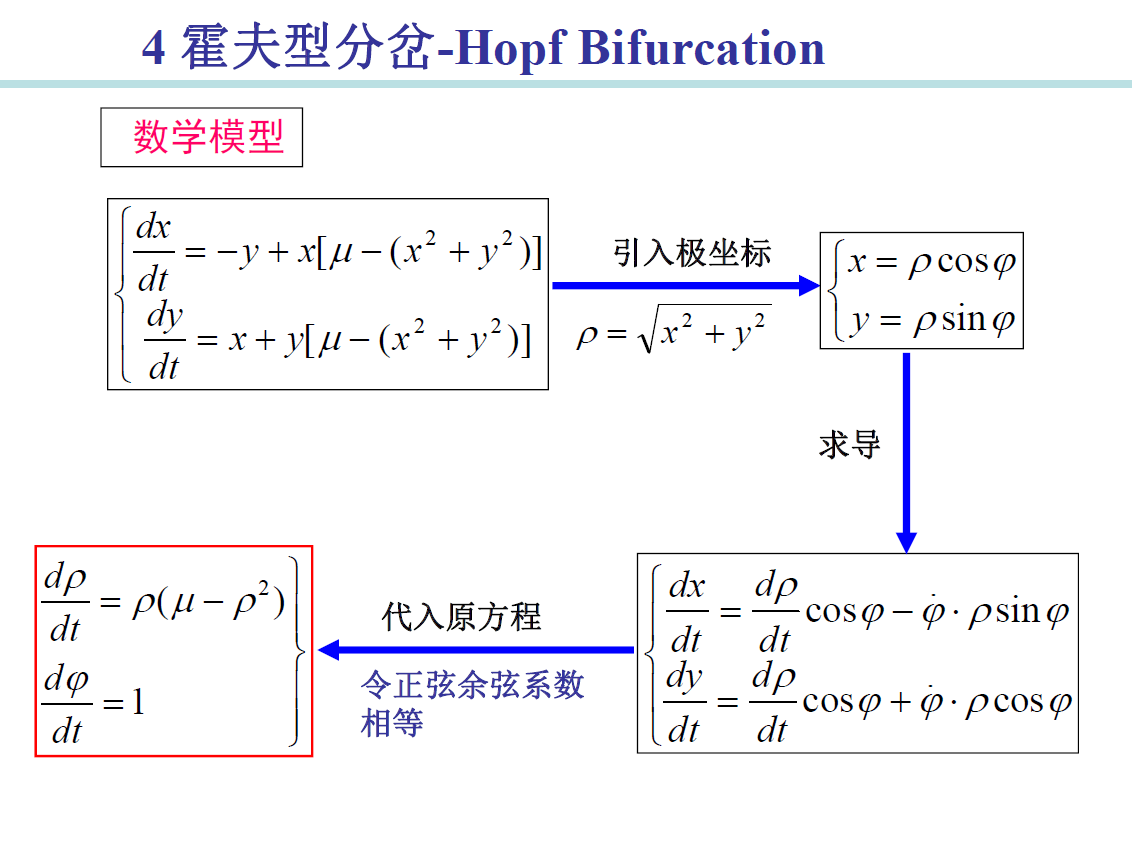

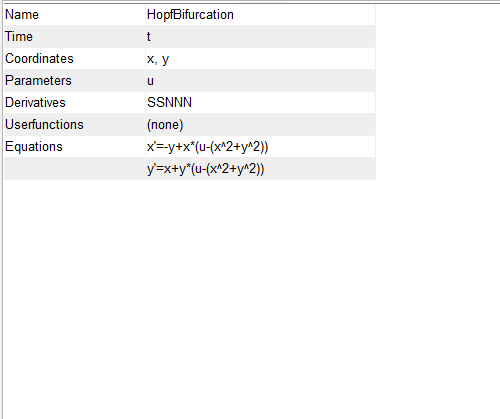
- u<0,收敛到静息态
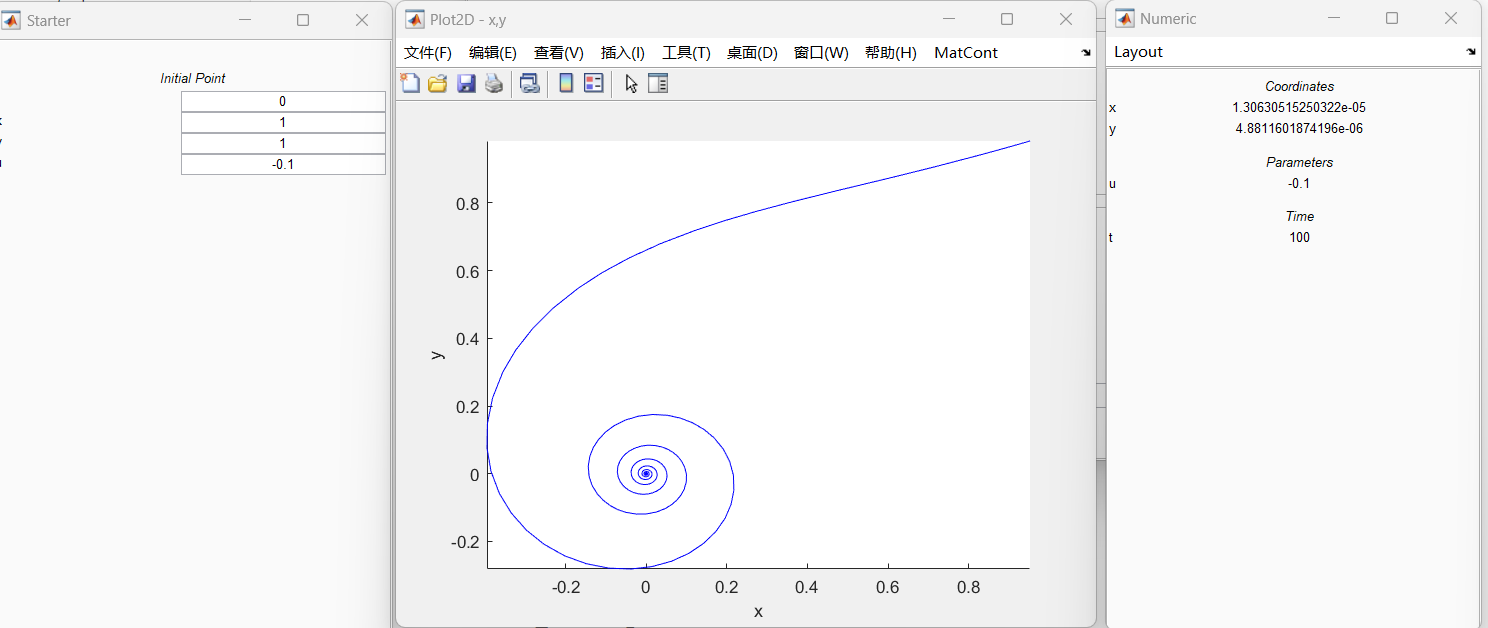
- u=0,缓慢收敛到静息态
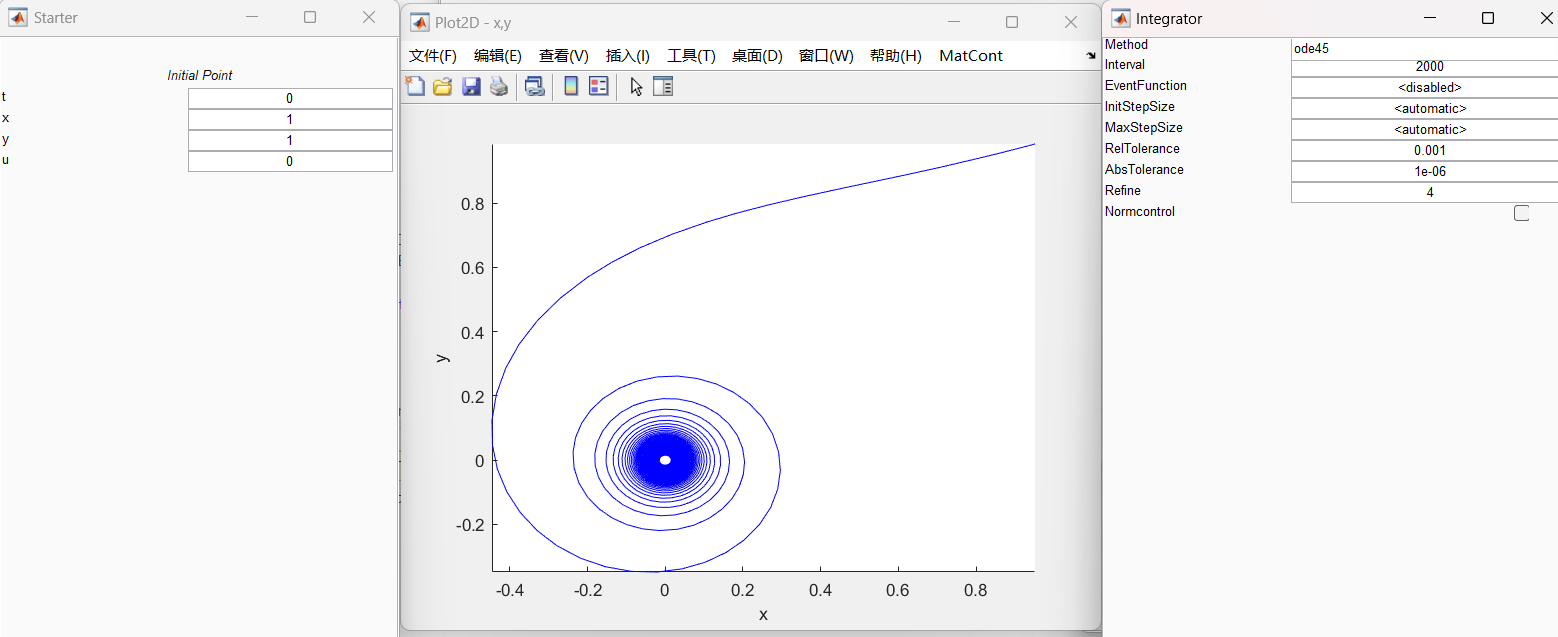
- u>0,收敛到极限环

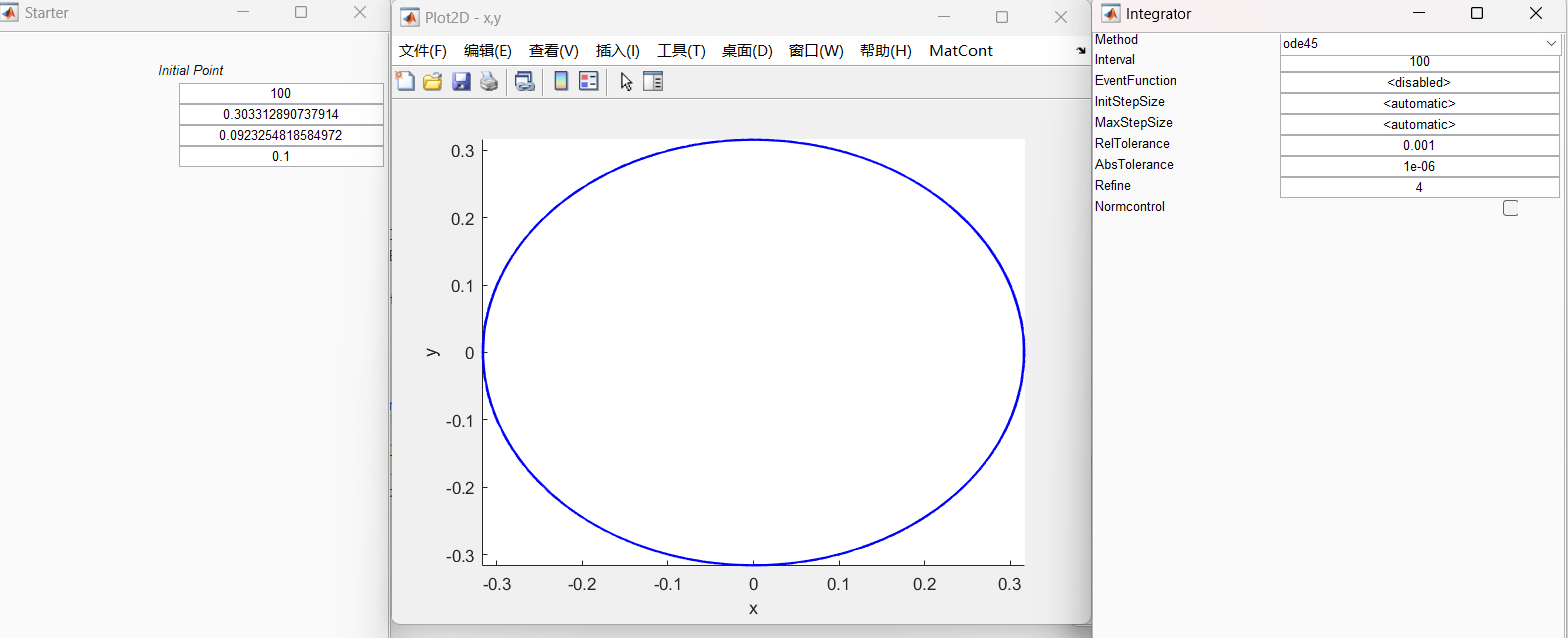
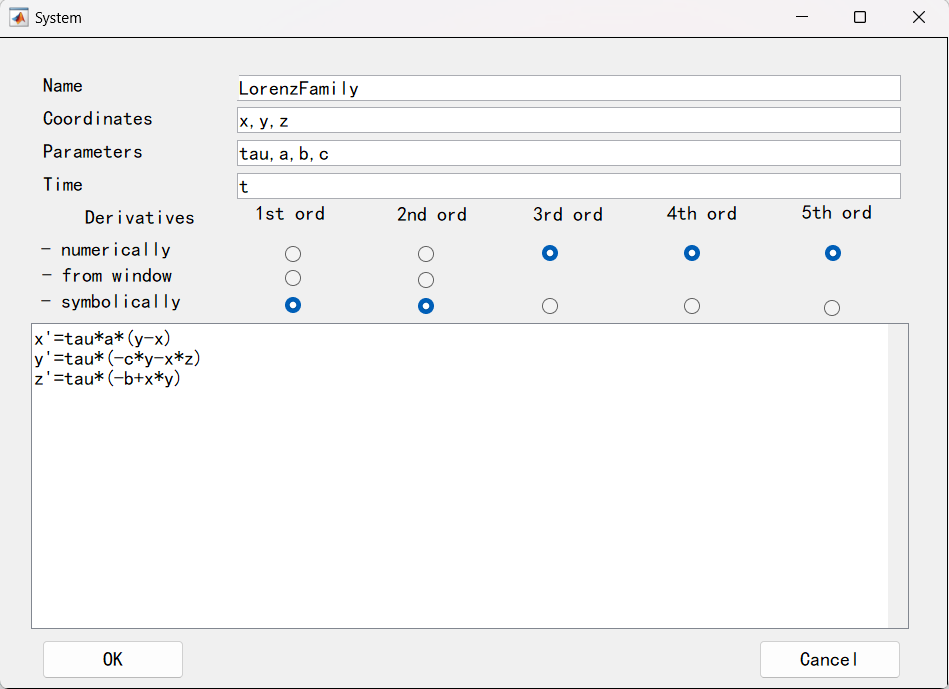
Lorenz_family

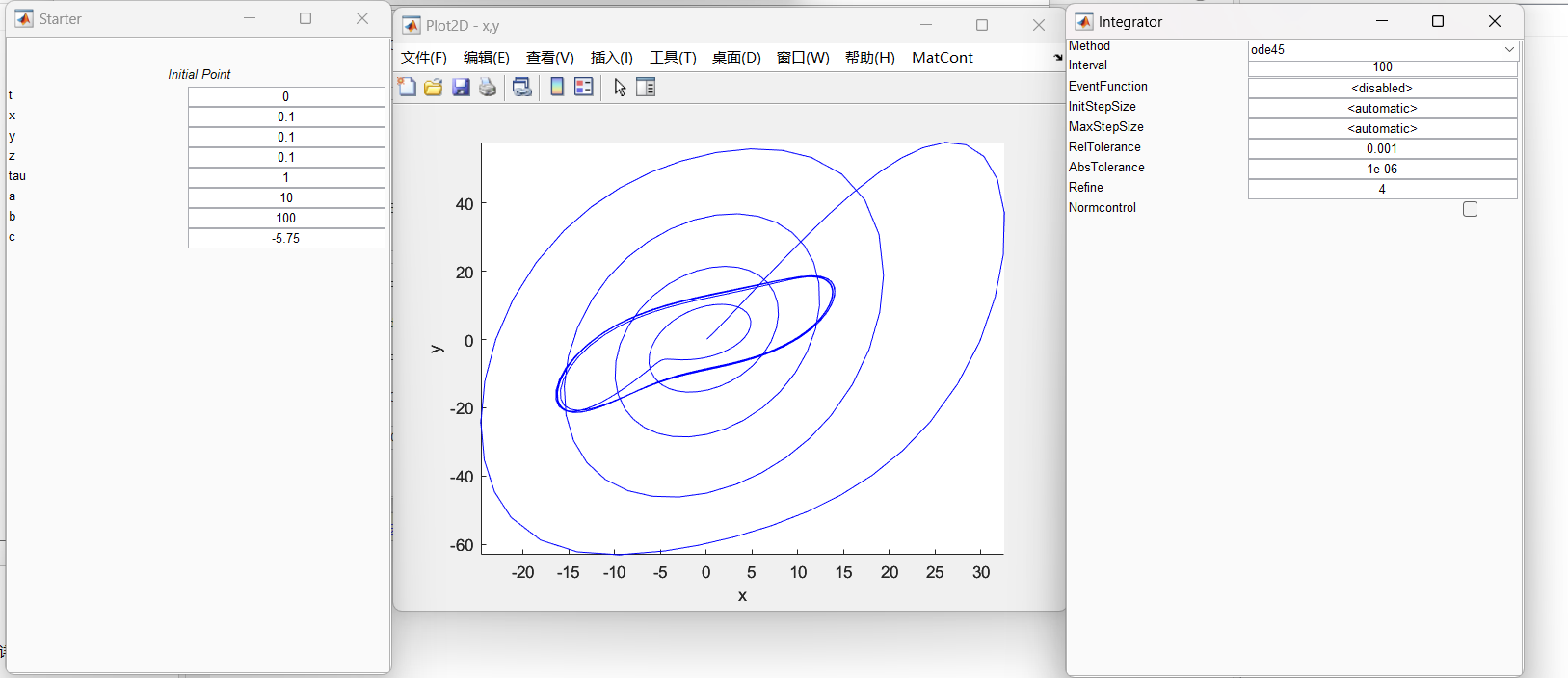
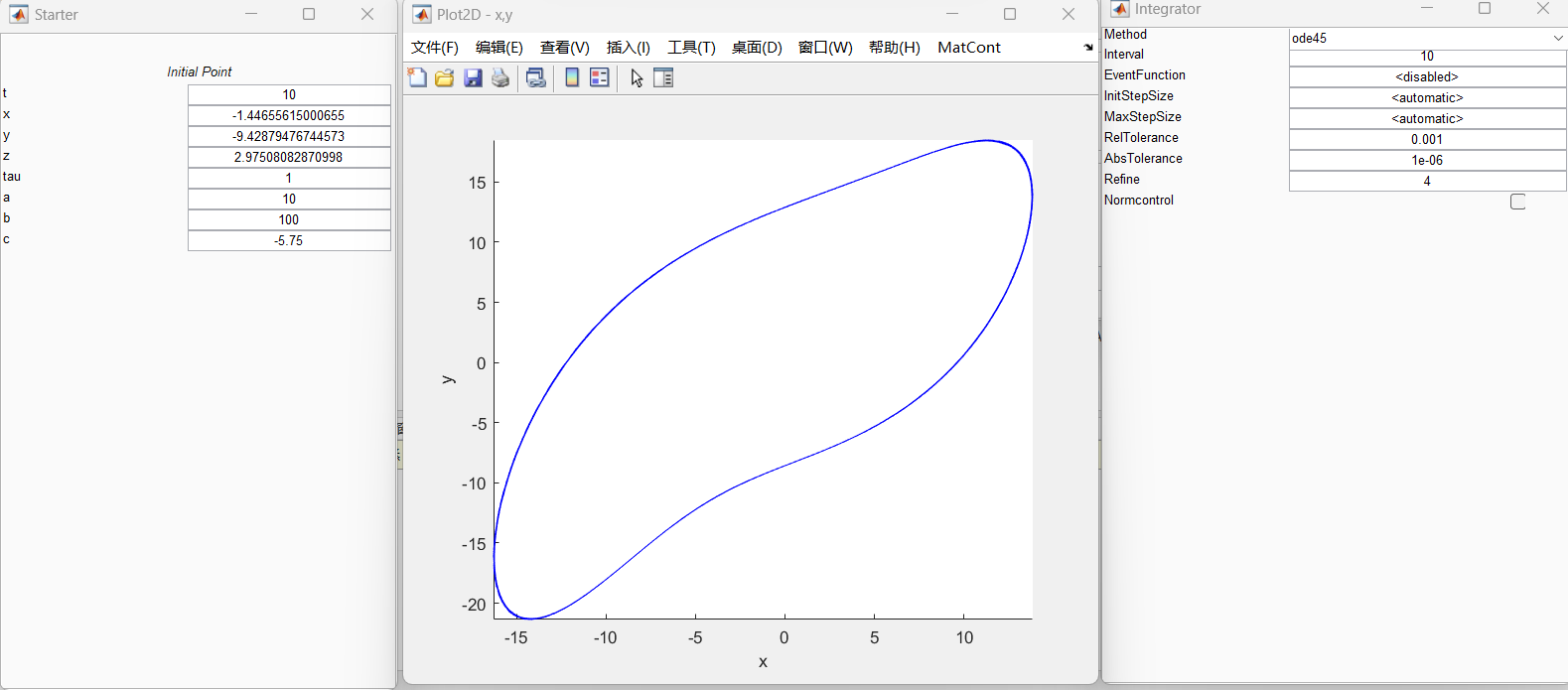
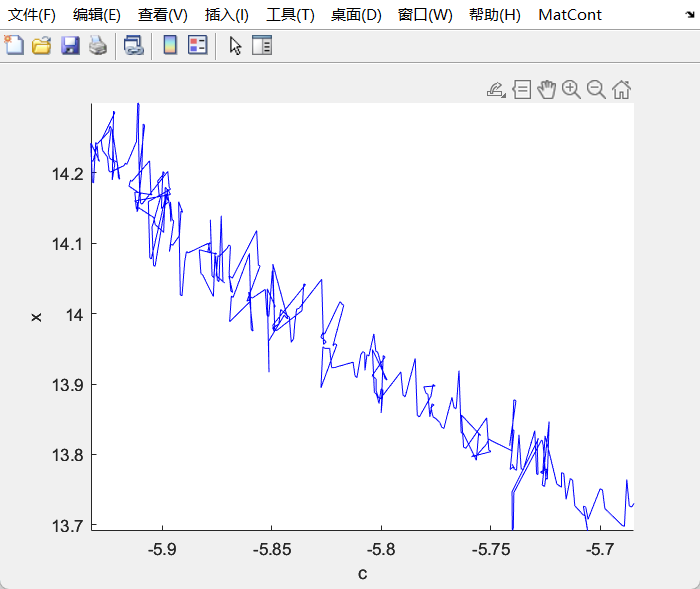

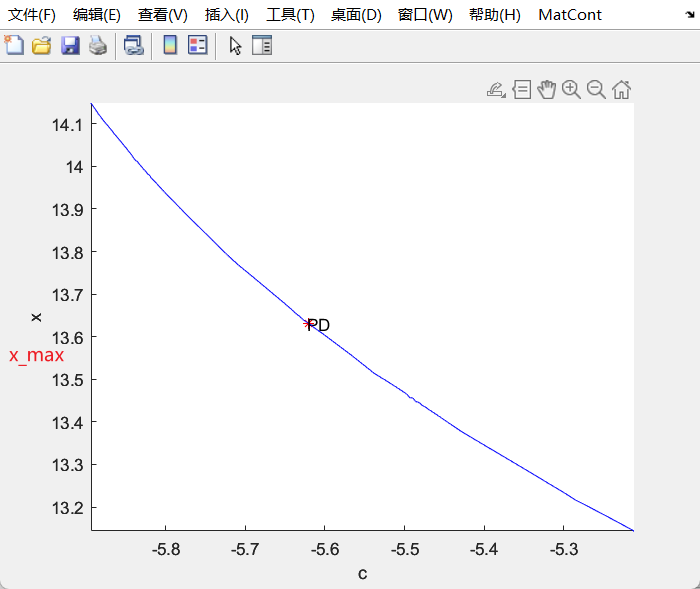
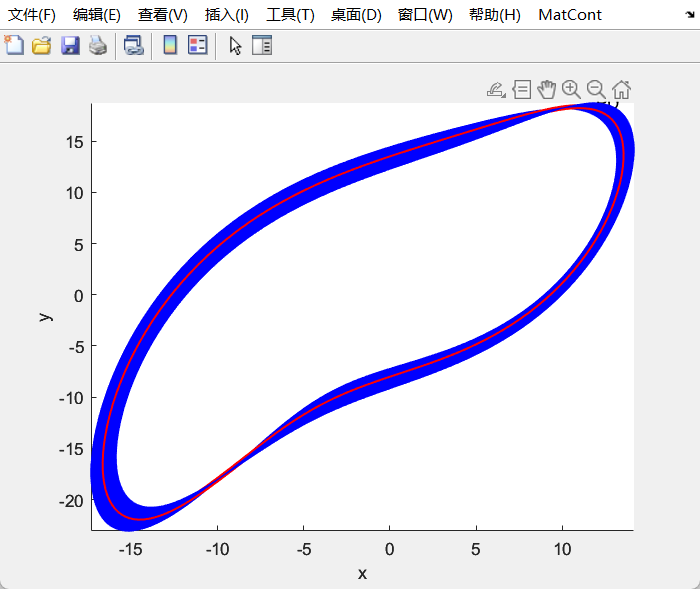
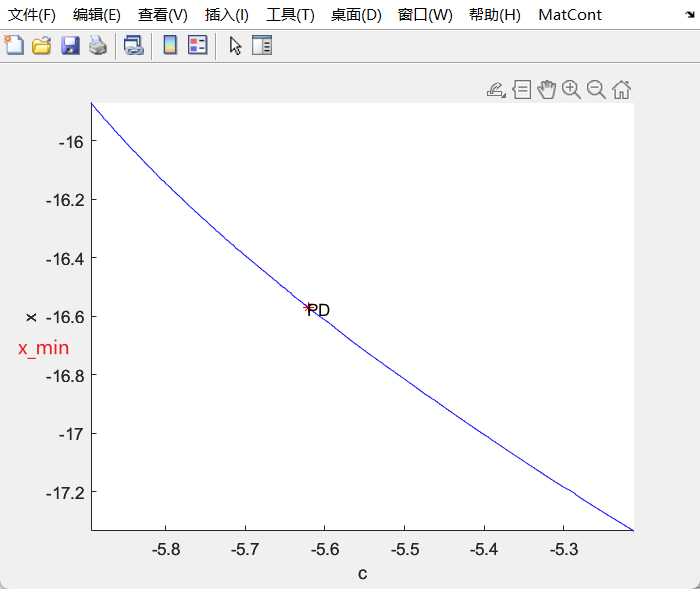

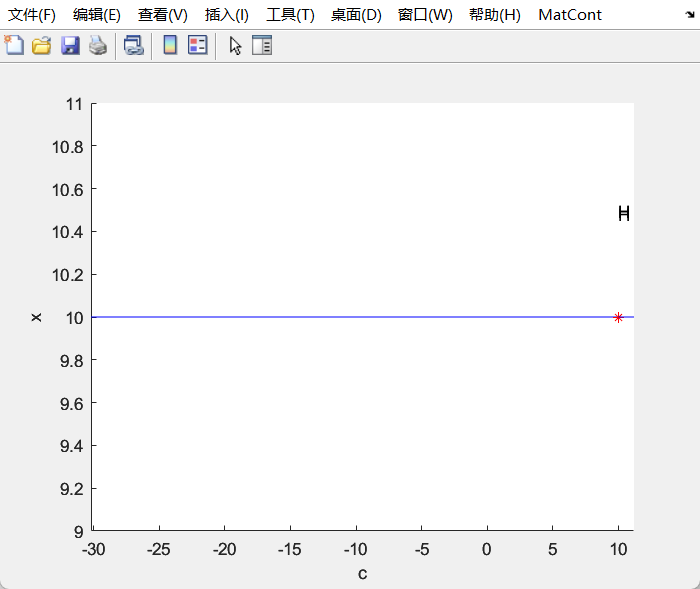
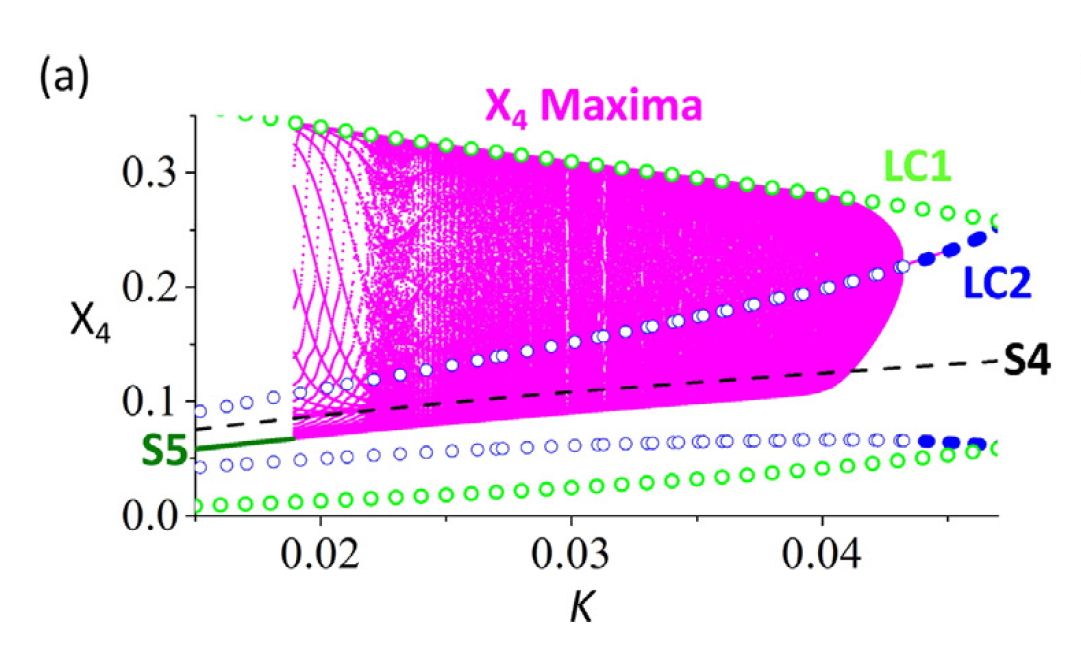
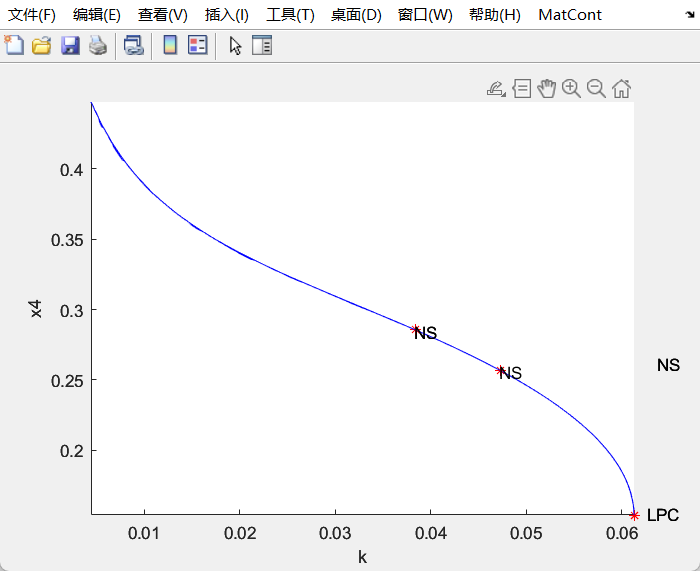
Bursting and complex oscillatory patterns in a gene regulatory network model

- 数学模型

x1'=(((x1+x3)^h)/((x1+x3)^h+k^h))*((k^h)/((x2+x4)^h+k^h))-x1x2'=(((x2+x3)^h)/((x2+x3)^h+k^h))*((k^h)/((x1+x4)^h+k^h))-x2x3'=(((x3)^h)/((x3)^h+k^h))*((k^h)/((x4)^h+k^h))-x3x4'=(((x3)^h)/((x3)^h+k^h))*((k^h)/((x1)^h+k^h))-x4


复现
figure 5
module Bursting_and_complex_oscillatory
implicit none
real(kind=8),parameter :: dt=0.005
integer,parameter :: MaxT=100000,T_trans=0,N=4
real(kind=8) :: x(N)
contains
subroutine x0()
implicit none
integer :: i
real(kind=8) :: x1,x2,x3,x4
call random_seed()
call random_number(x(1))
call random_number(x(2))
call random_number(x(3))
call random_number(x(4))
write(10,*) x(1),x(2),x(3),x(4)
end subroutine x0
subroutine fnf(xx,fx)
implicit none
real(kind=8) :: xx(N),fx(N)
real(kind=8) :: h,k
h=2.0
k=0.0185
fx(1)=((x(1)+x(3))**h/((x(1)+x(3))**h+k**h))*(k**h/((x(2)+x(4))**h+k**h))-x(1)
fx(2)=((x(2)+x(3))**h/((x(2)+x(3))**h+k**h))*(k**h/((x(1)+x(4))**h+k**h))-x(2)
fx(3)=((x(3))**h/((x(3))**h+k**h))*(k**h/((x(4))**h+k**h))-x(3)
fx(4)=((x(3))**h/((x(3))**h+k**h))*(k**h/(x(1)**h+k**h))-x(4)
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real(kind=8) :: x(N),xx(N),fx(N)
real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
xx=x
call fnf(xx,fx)
kx1=dt*fx
xx=x+0.5*kx1
call fnf(xx,fx)
kx2=dt*fx
xx=x+0.5*kx2
call fnf(xx,fx)
kx3=dt*fx
xx=x+kx3
call fnf(xx,fx)
kx4=dt*fx
x=x+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
return
end subroutine rk4
end module Bursting_and_complex_oscillatory
program main
use Bursting_and_complex_oscillatory
implicit none
integer :: t,i,j
open(10,file="x0.txt")
open(20,file="t_x.txt")
call x0()
do t=1,MaxT,1
call rk4(x)
if(t>=T_trans) then
write(20,"(5(F15.6))") t*dt,x(1),x(2),x(3),x(4)
end if
end do
close(10)
close(20)
end program main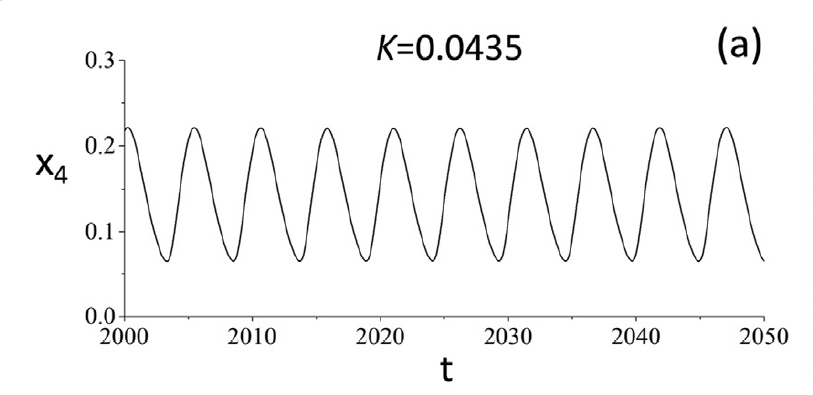
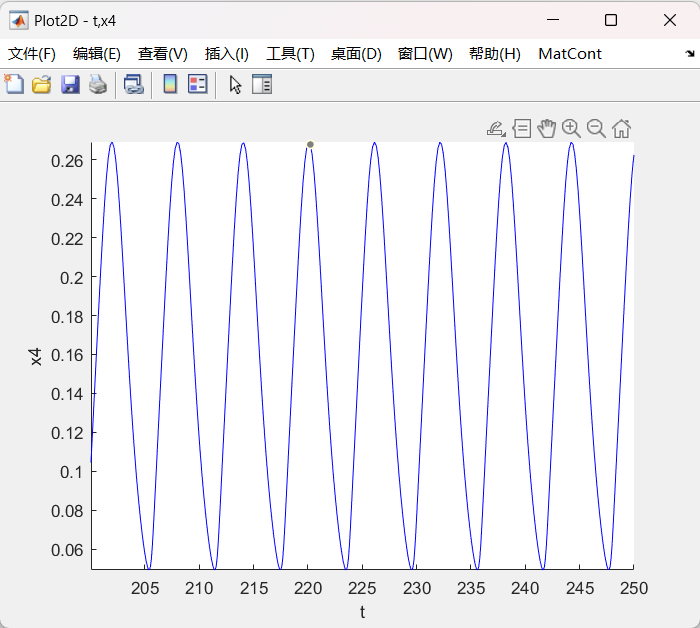
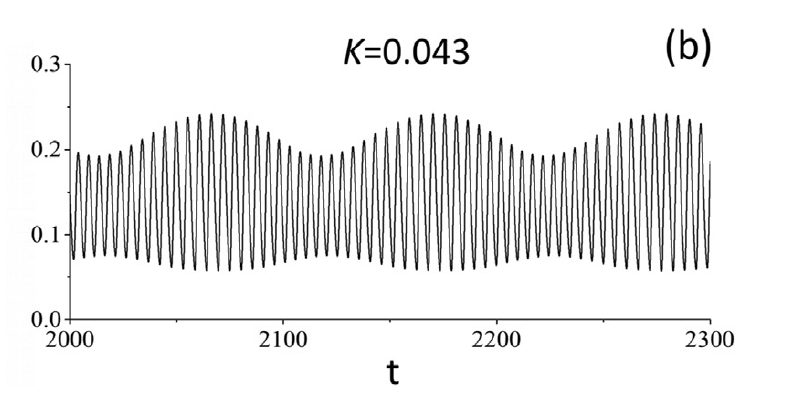
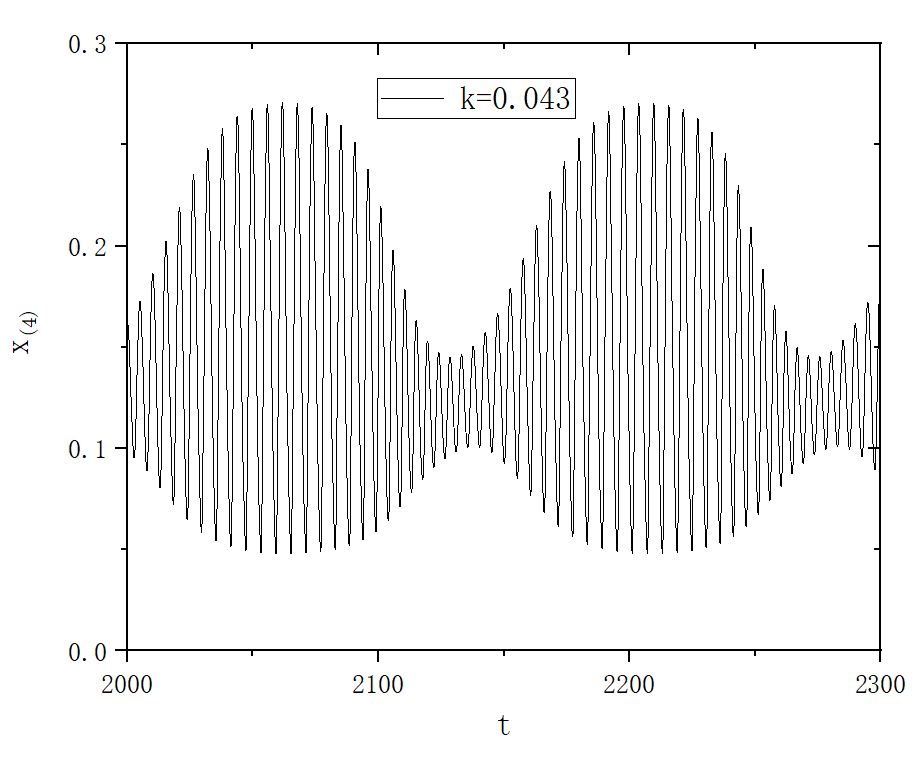

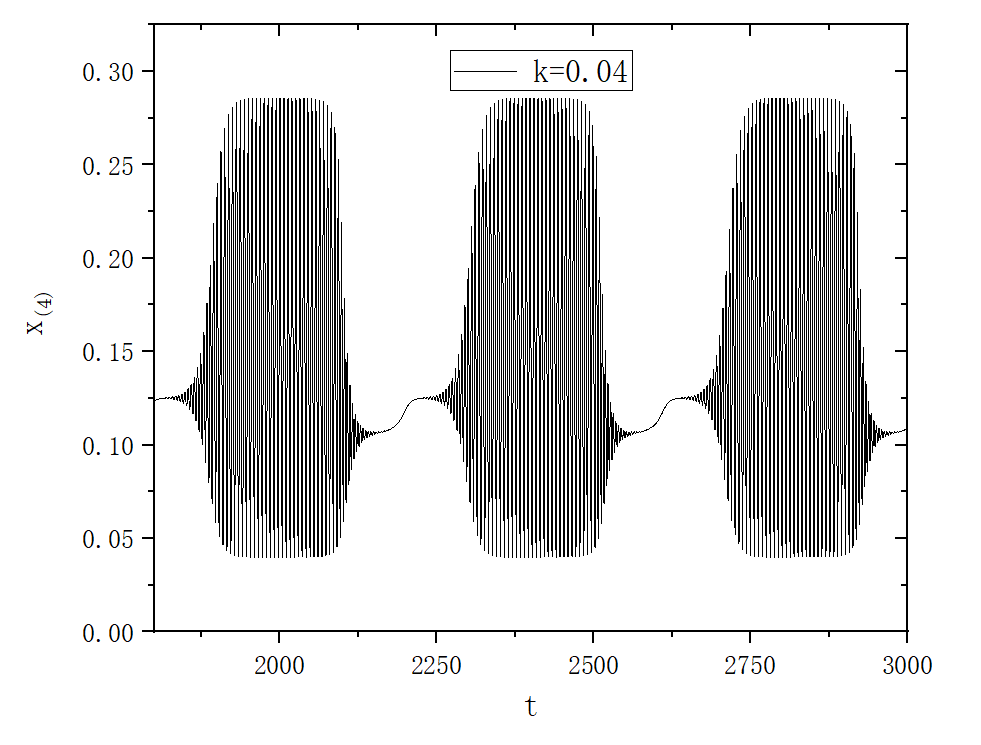
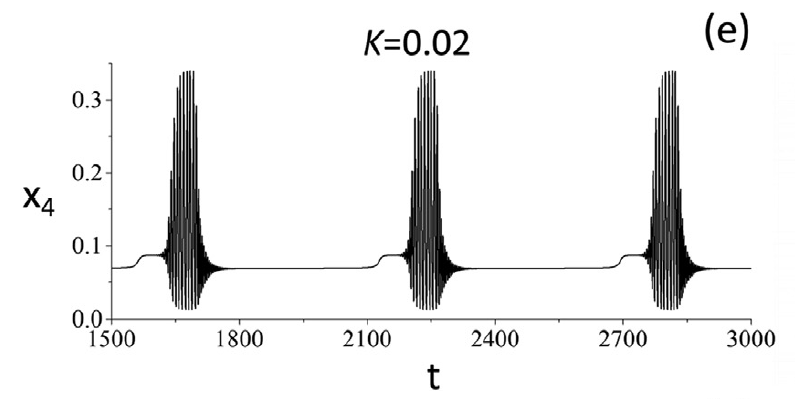
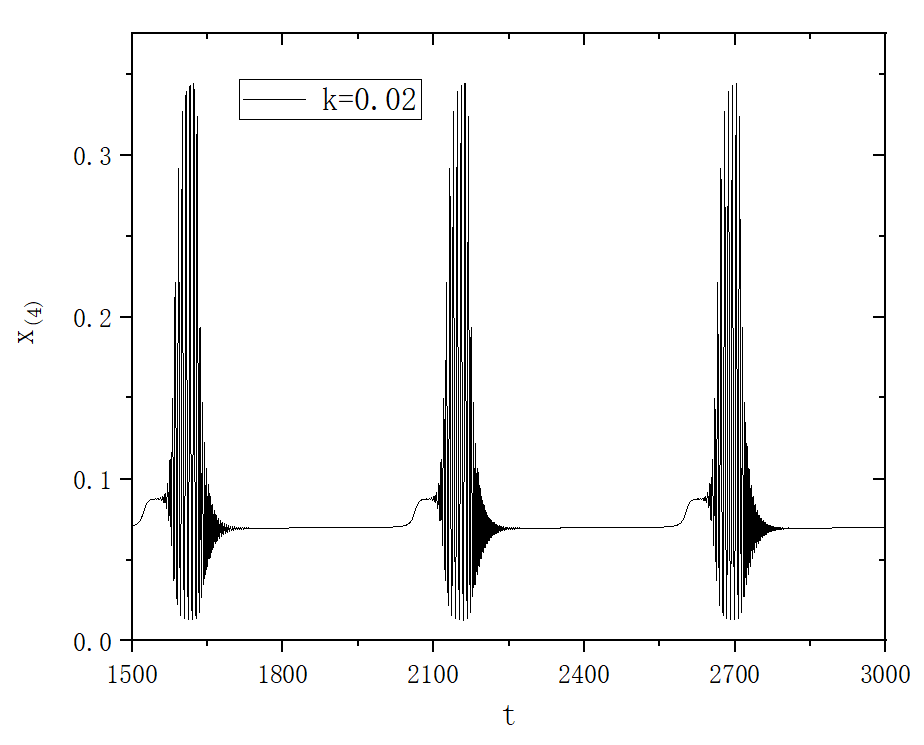
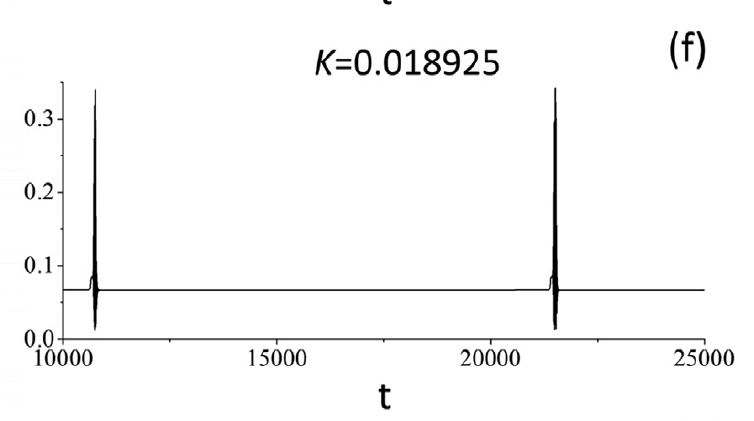
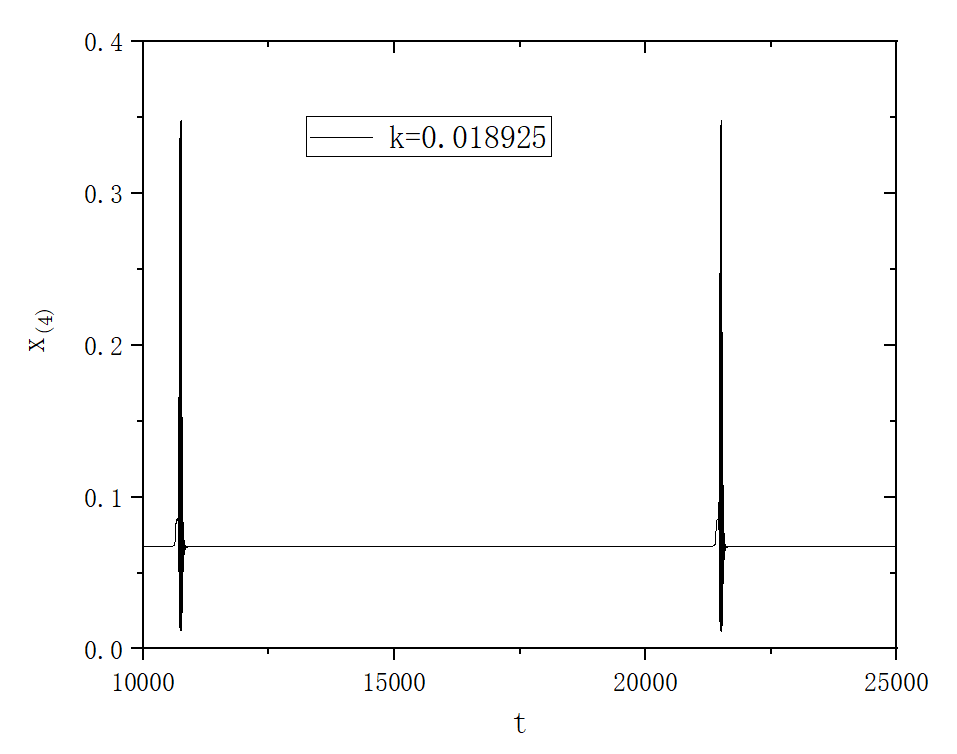
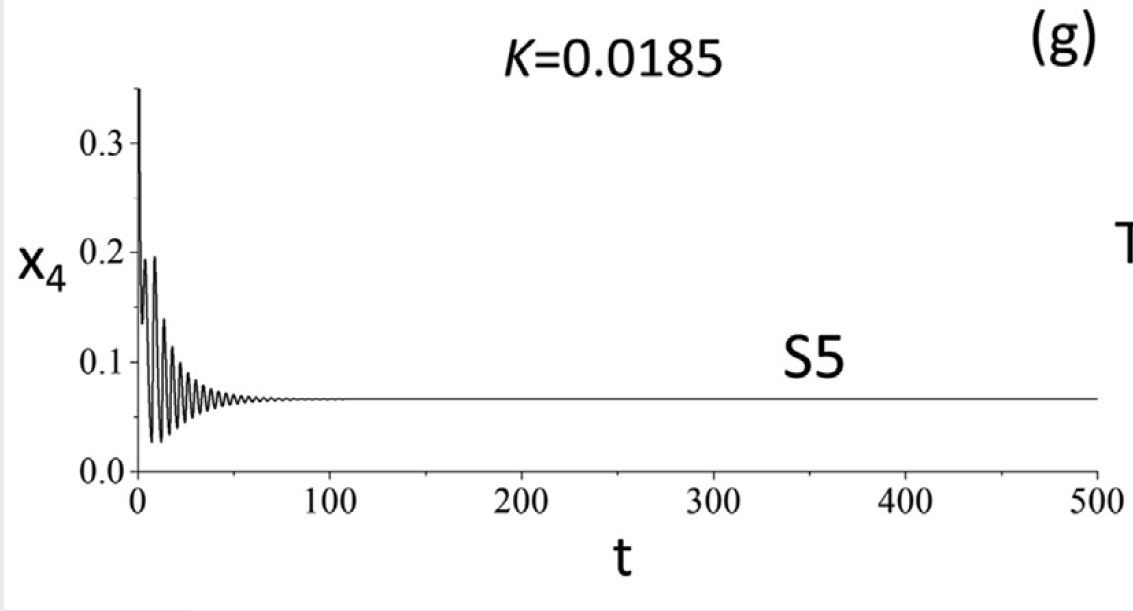

figure 3