排斥耦合混沌振子中的稳定振幅奇异态和死亡奇异态

Stable amplitude chimera states and chimera death in repulsively coupled chaotic oscillators

阅读

下载地址：

复现

figure 1

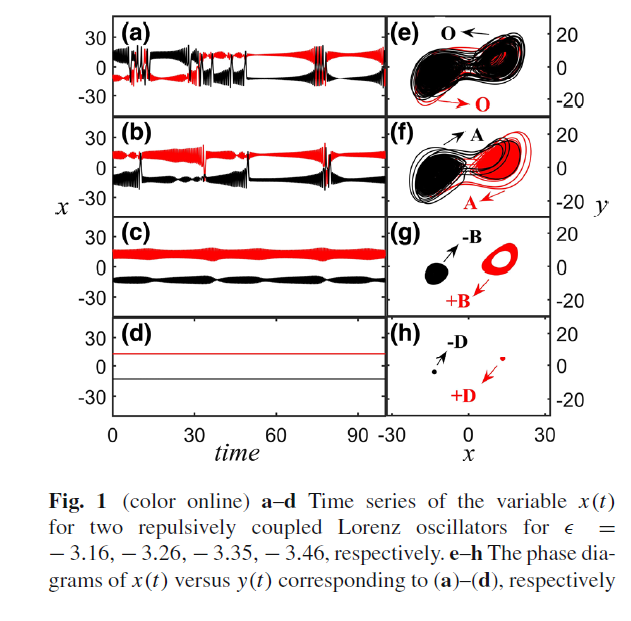
module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=2500000,T_trans=2000000,N=3,M=2
    real(kind=8) :: x(M,N)
    integer :: p=1
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-3.16
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_1.txt")
    open(50,file="t_x_y_z_2.txt")
    max=-1000.0
    min=1000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(2,1),x(2,2),x(2,3)
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main

figure 1_A

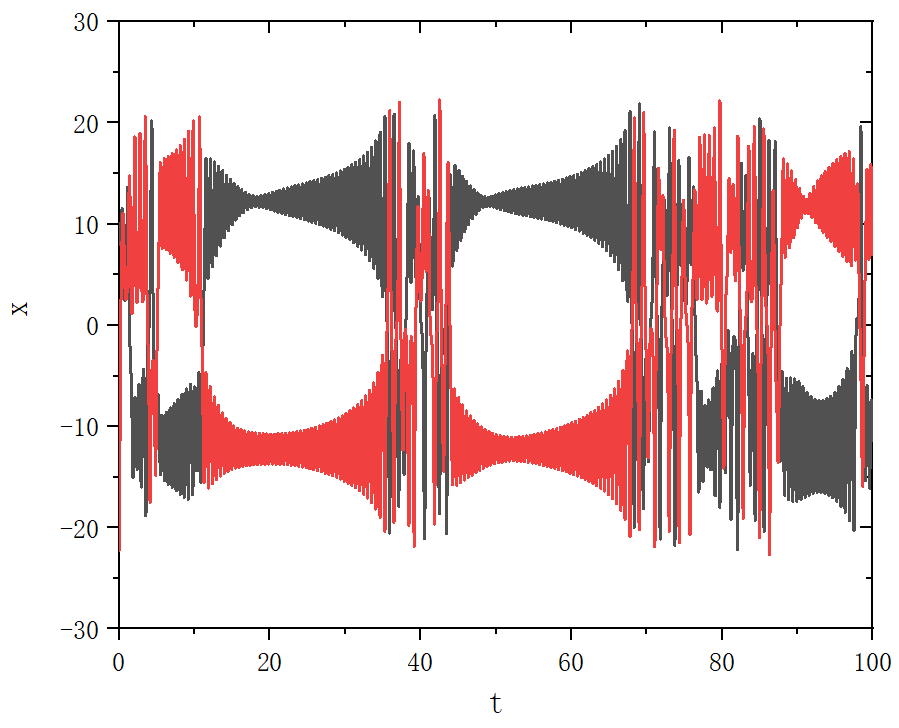
figure 1_B

figure 1_C

figure 1_D

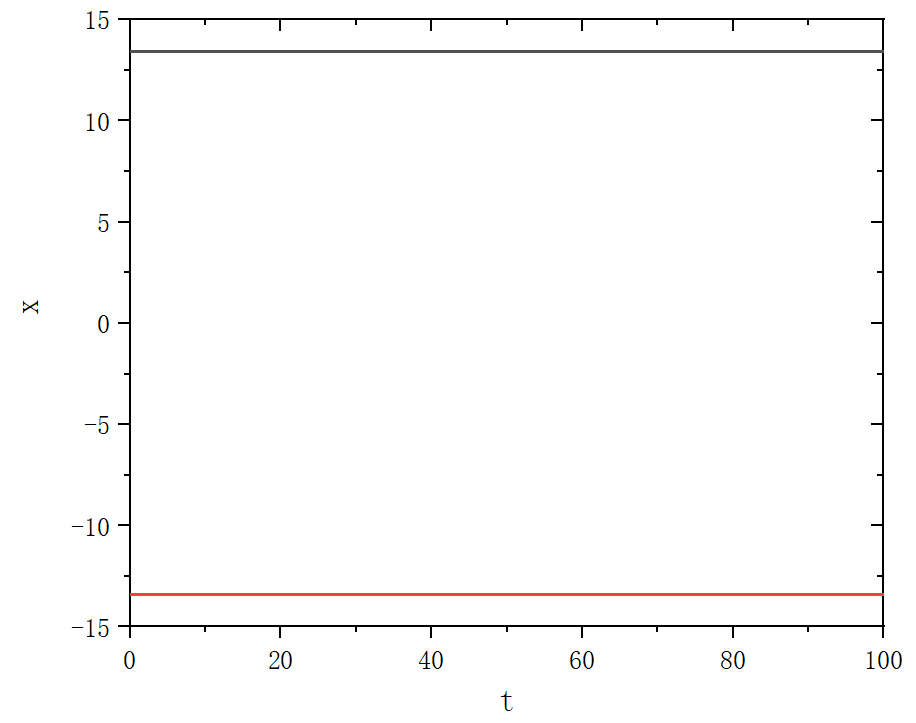
figure 1_E

figure 1_F

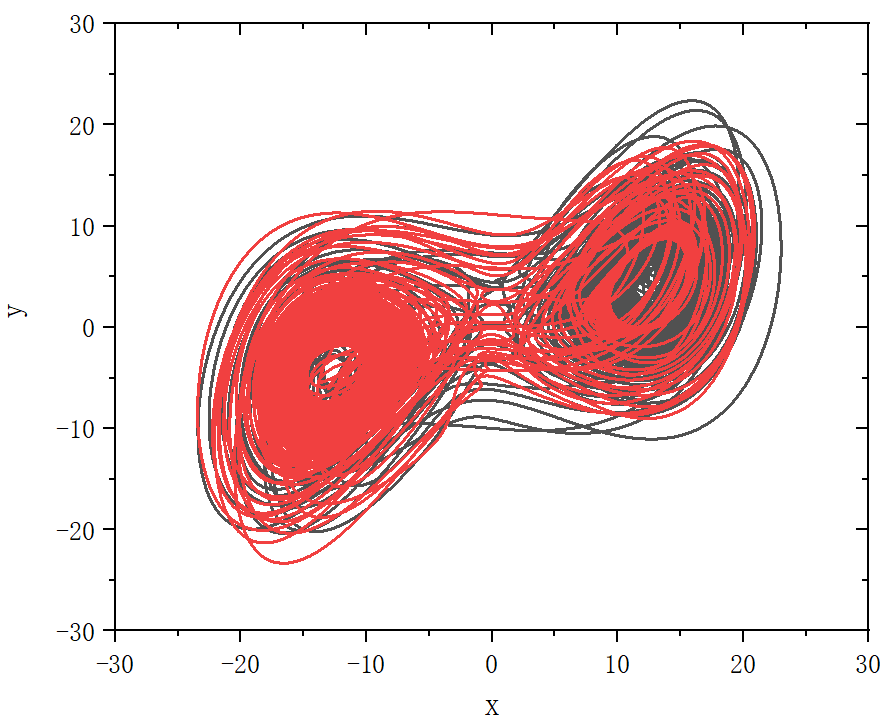
figure 1_G

figure 1_H

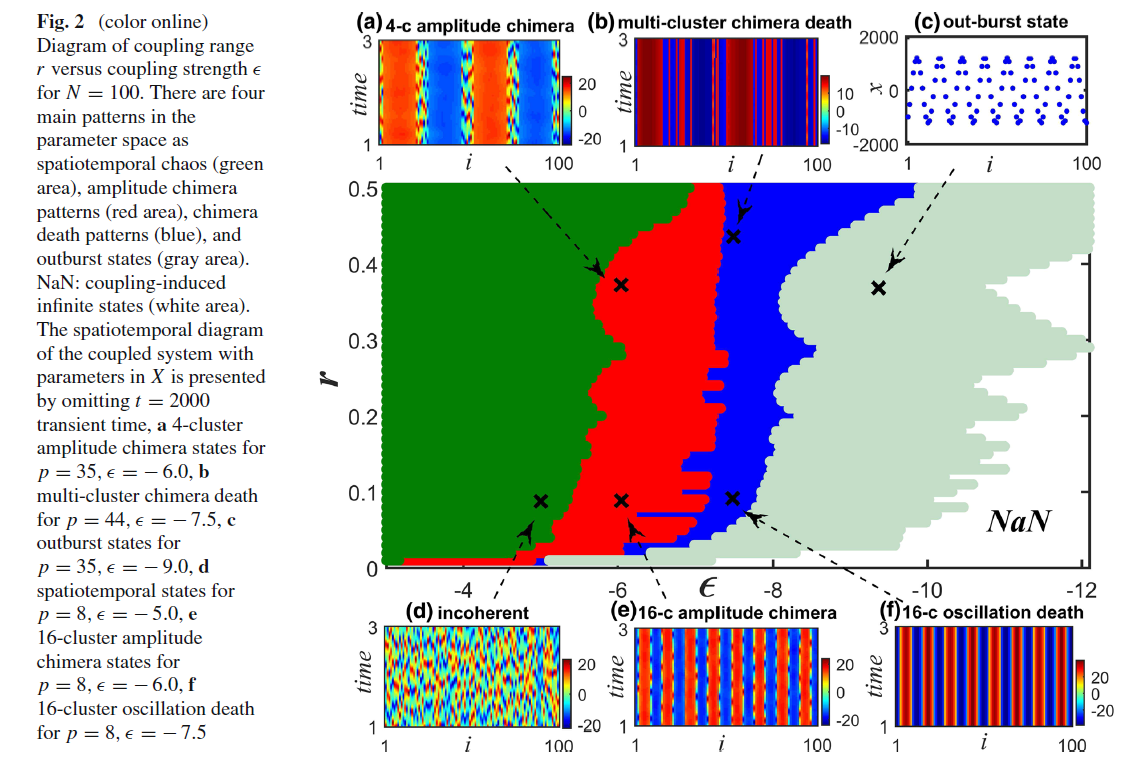
figure 2

module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=2006000,T_trans=2003000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p=35
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-6.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_1.txt")
    open(50,file="t_x_y_z_2.txt")
    open(60,file="i_t_x_y_z.txt")
    max=-1000.0
    min=1000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(2,1),x(2,2),x(2,3)
            do i=1,M,1
                if(mod(t,1)==0) then
                    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if    
            end do    
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main

figure 2_A

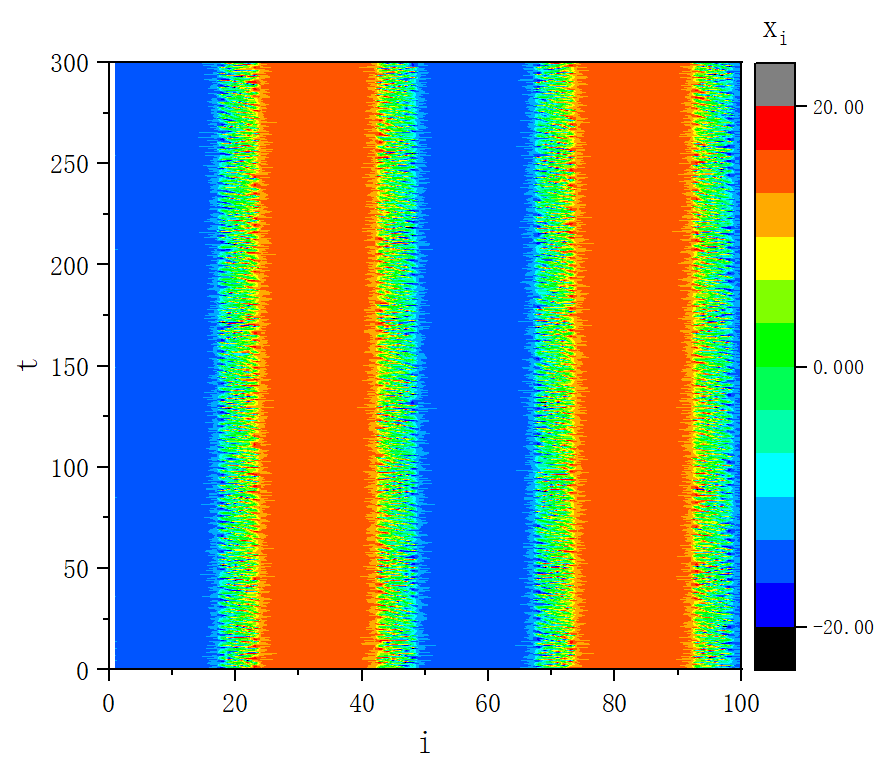
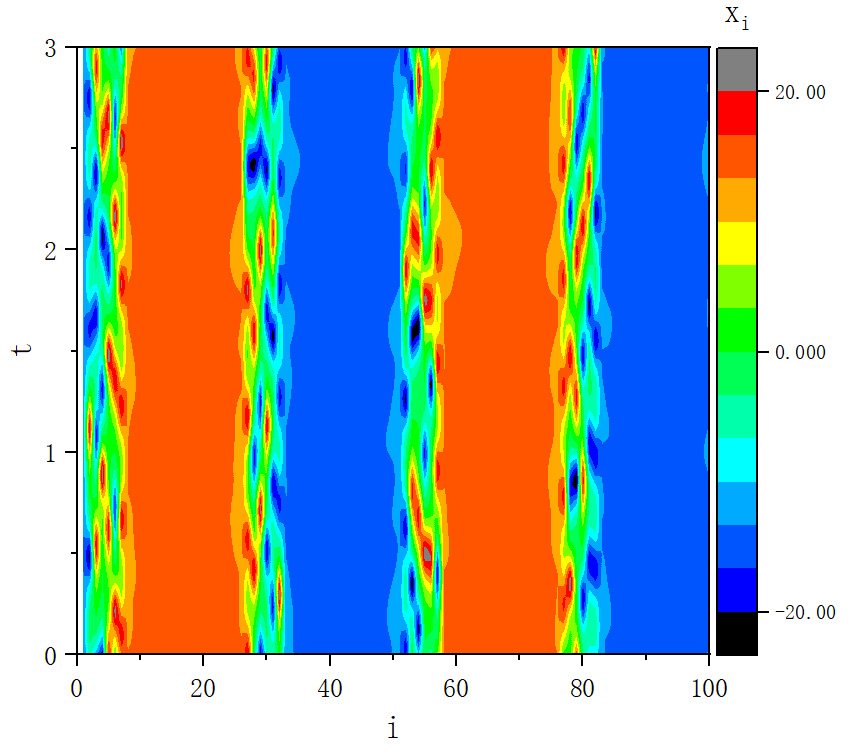
figure 2_B

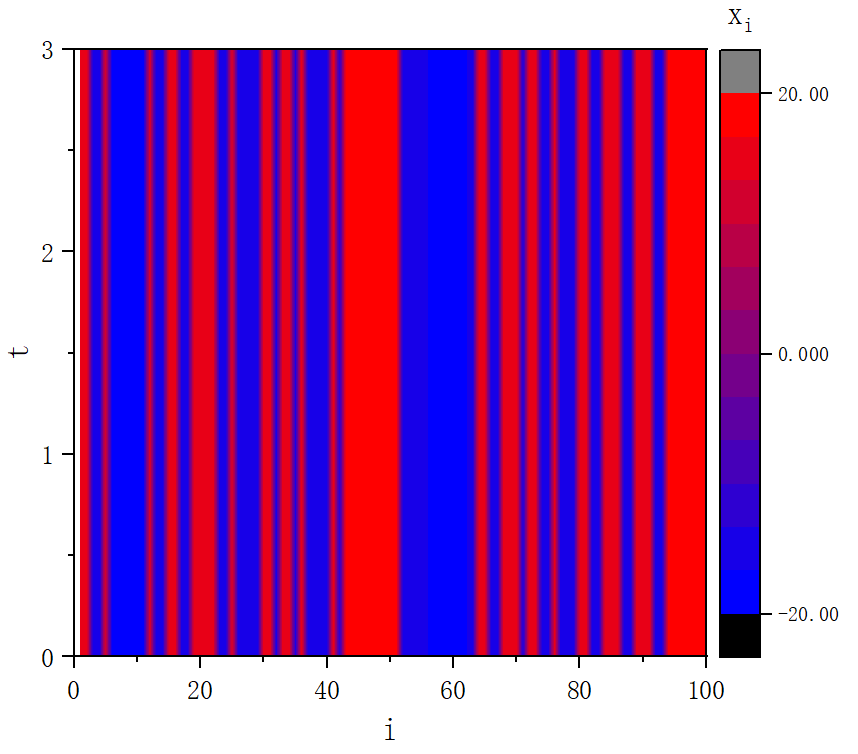
figure 2_C

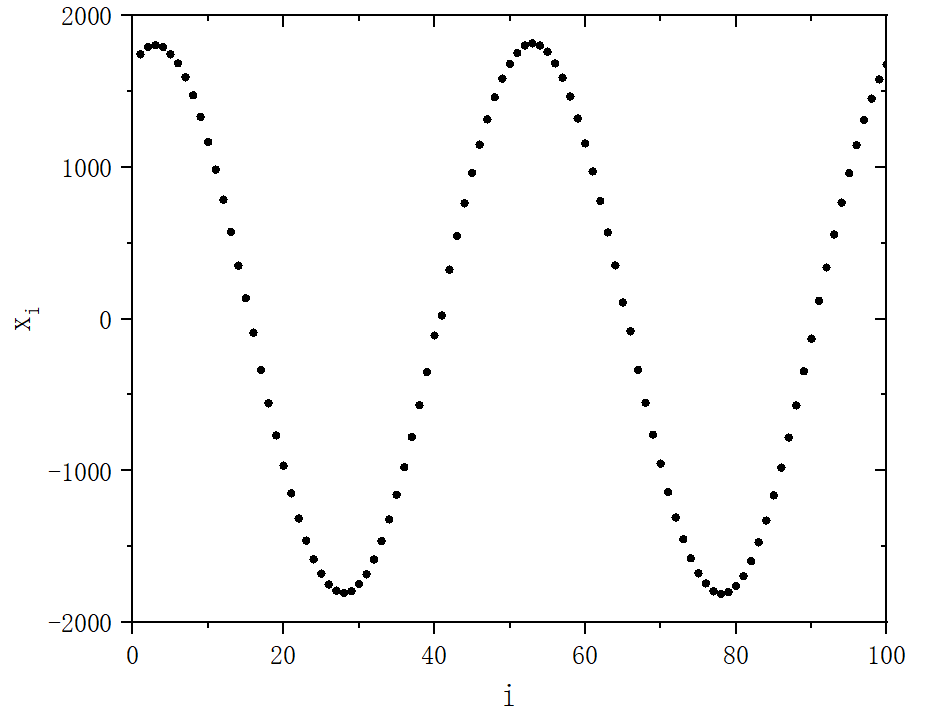
figure 2_D

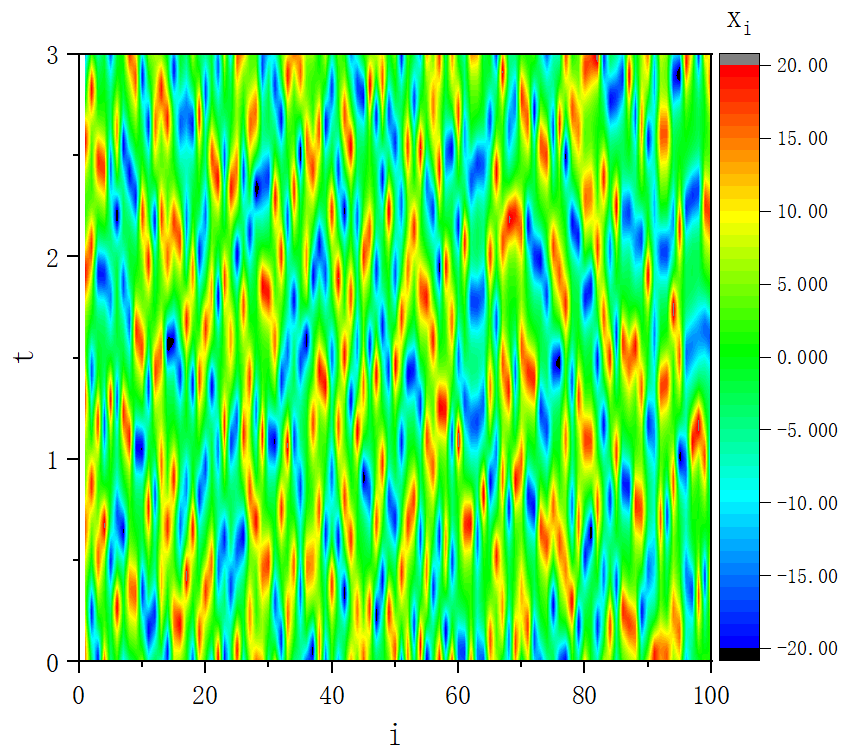
figure 2_E

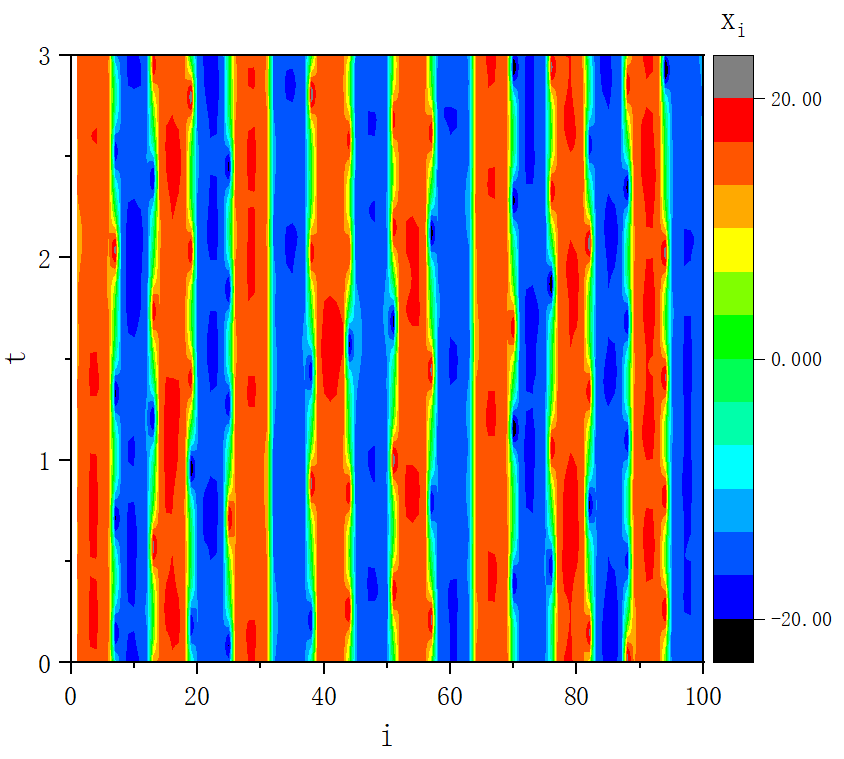
figure 2_F

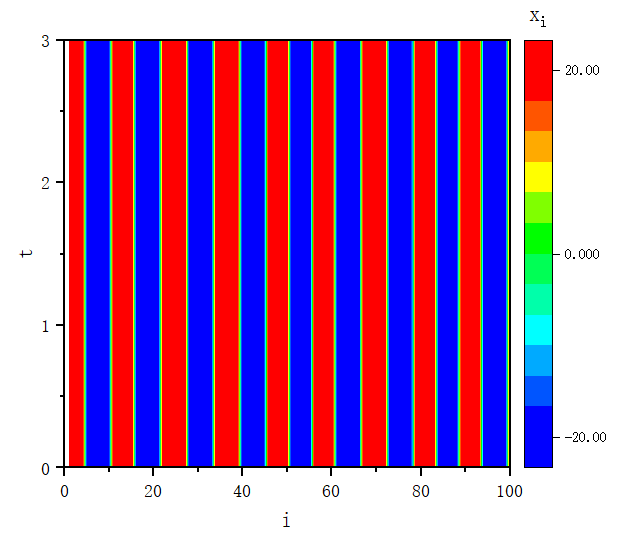
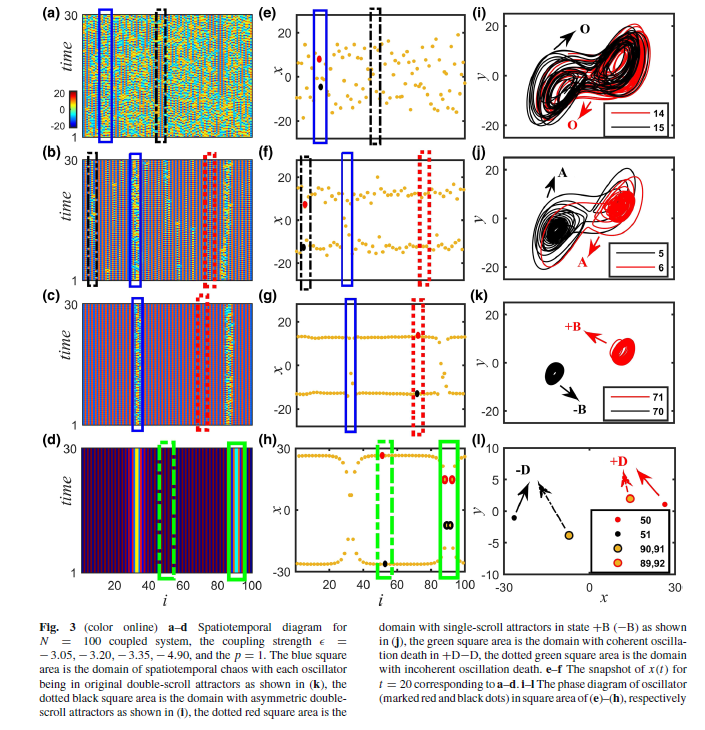
figure 3

module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=2030000,T_trans=2000000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p=1
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-3.05
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    max=-10000.0
    min=10000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
            do i=1,M,1
                if((t-T_trans)*h==20) then
                    write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
                if(mod(t,50)==0) then
                    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
            end do
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main

figure 3_A

figure 3_B

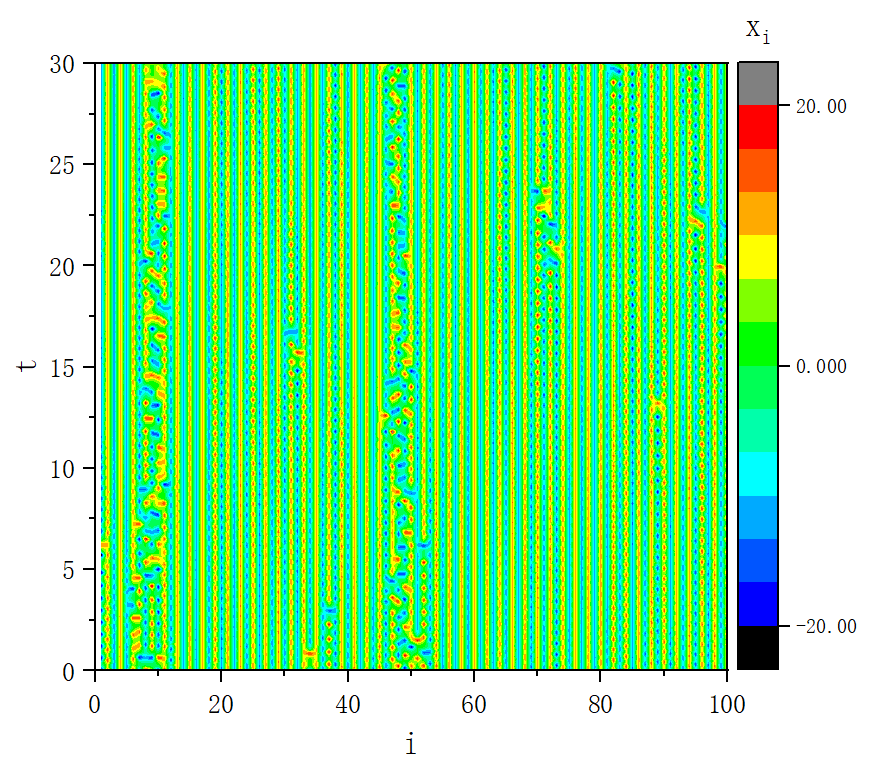
figure 3_C

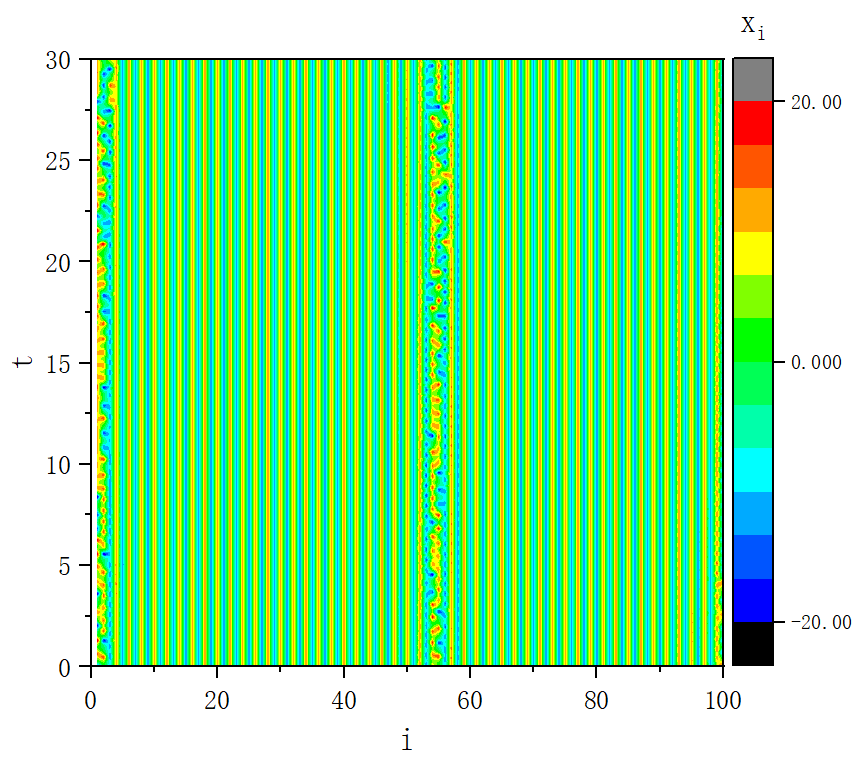
figure 3_D

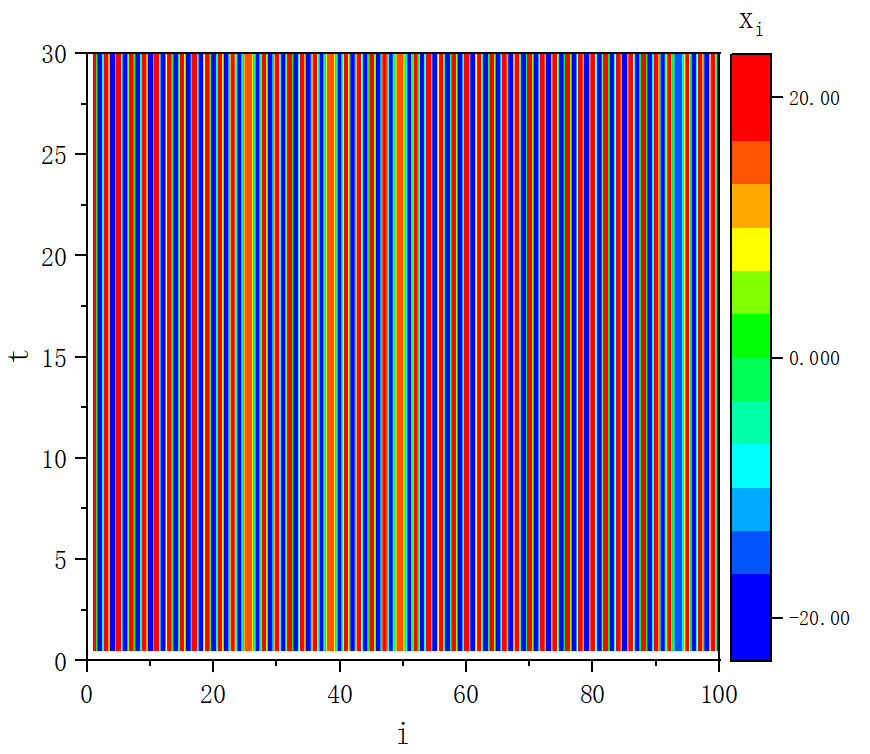
figure 3_E

figure 3_F

figure 3_G

figure 3_H

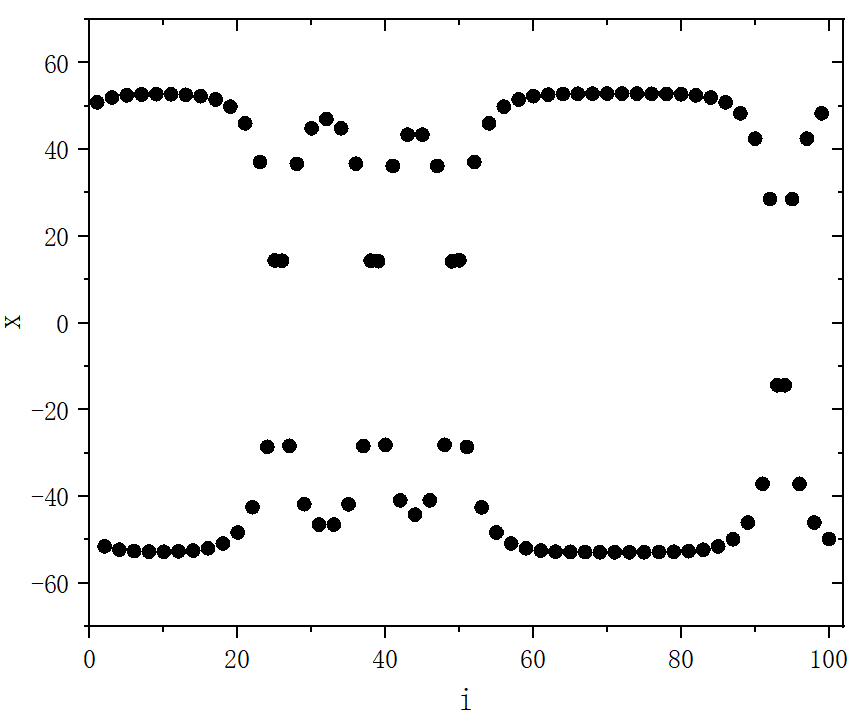
figure 3_I

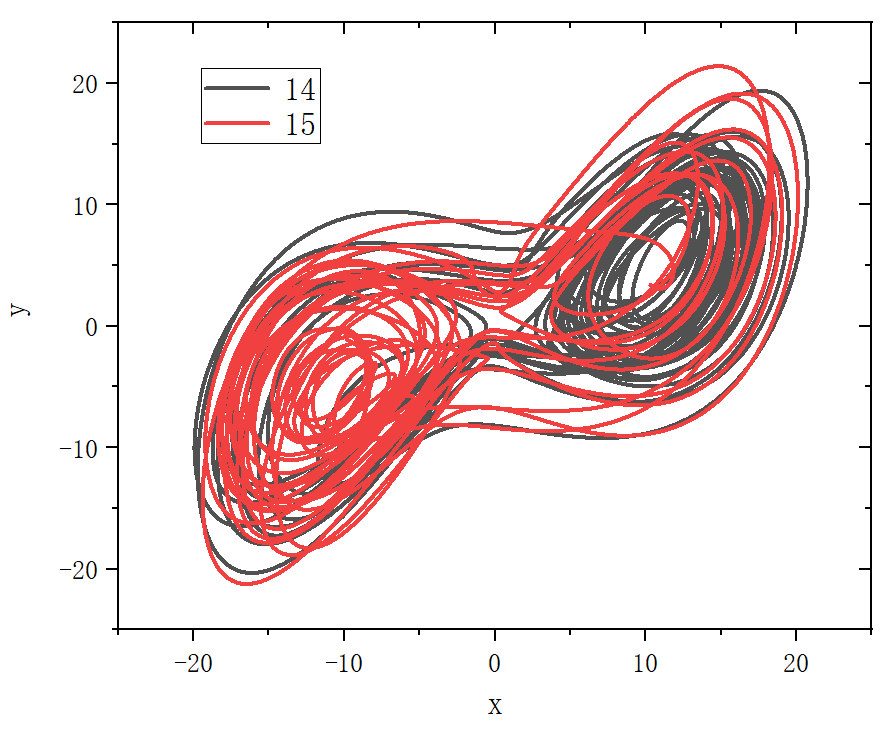
figure 3_J

figure 3_K

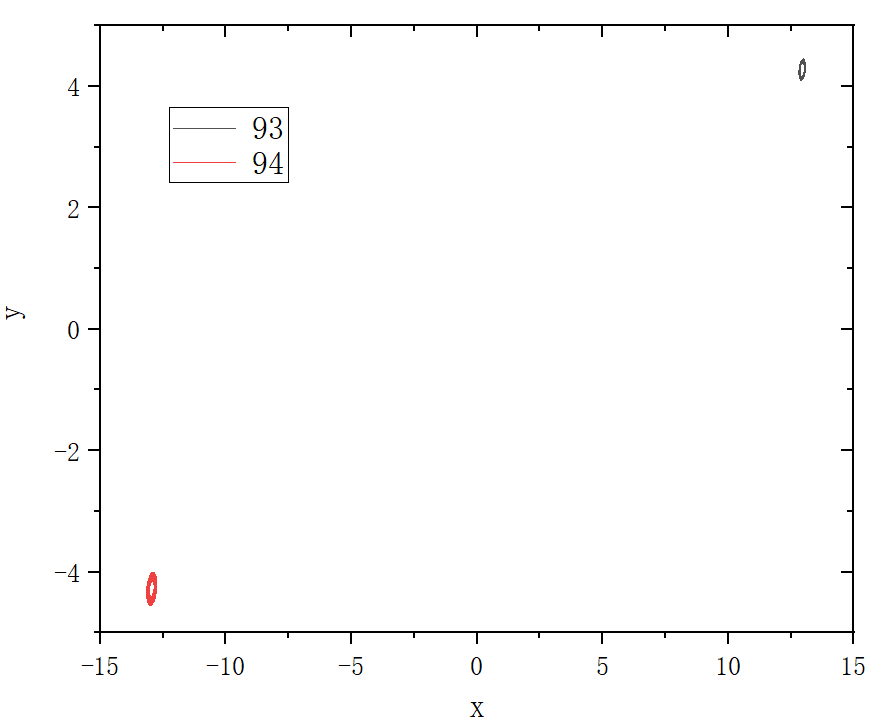
figure 3_L

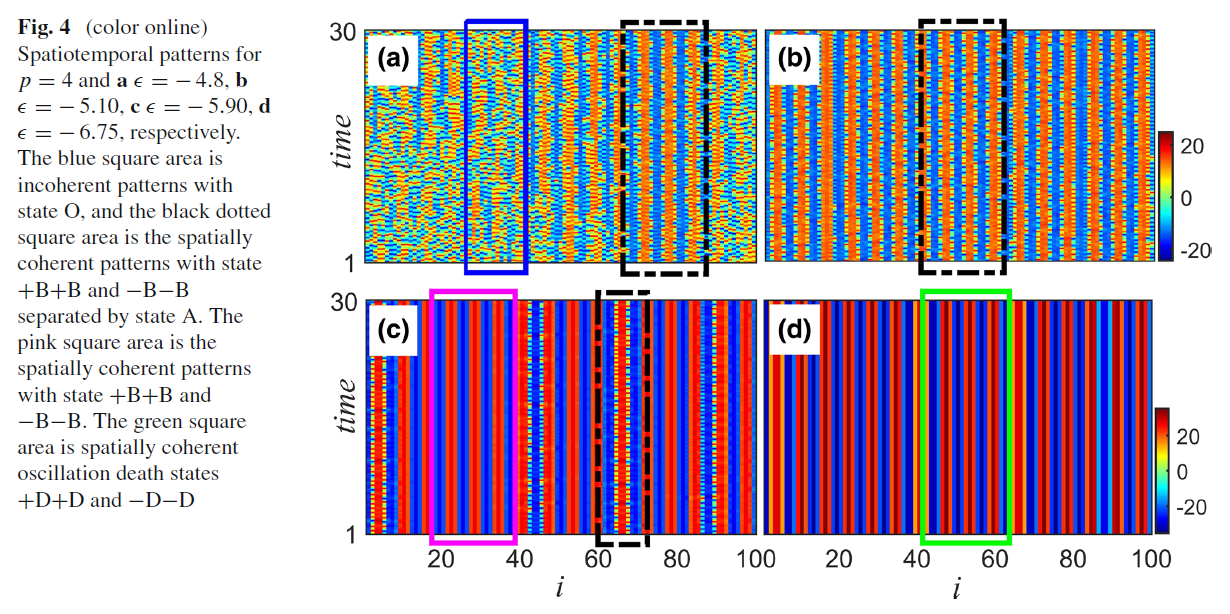
figure 4

module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=2030000,T_trans=2000000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p=4
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-5.90
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    max=-10000.0
    min=10000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
            do i=1,M,1
                write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                if((t-T_trans)*h==20) then
                    write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
                if(mod(t,50)==0) then
                    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
            end do
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main

figure 4_A

figure 4_B

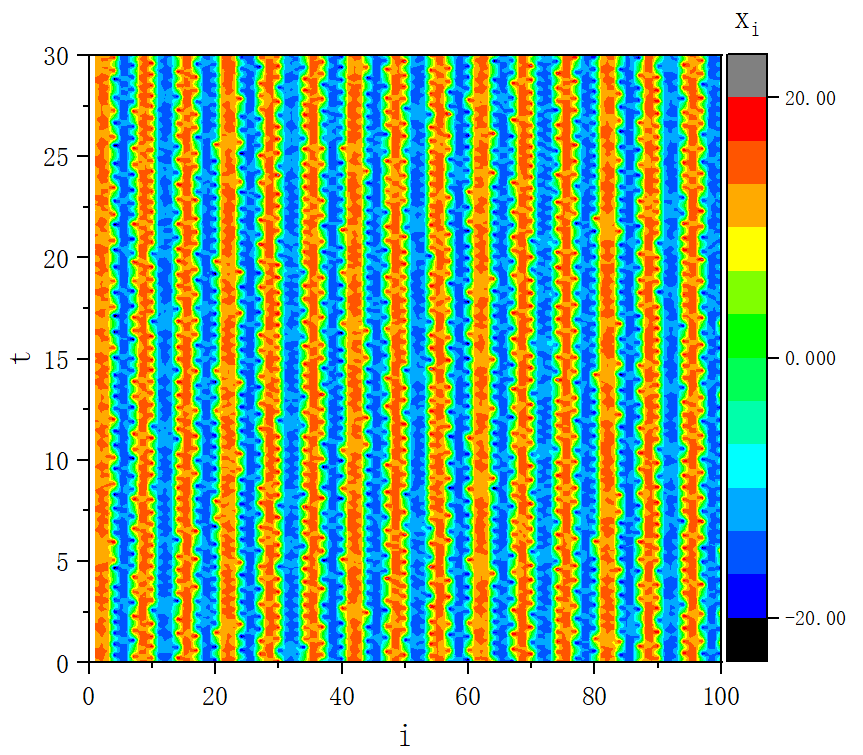
figure 4_C

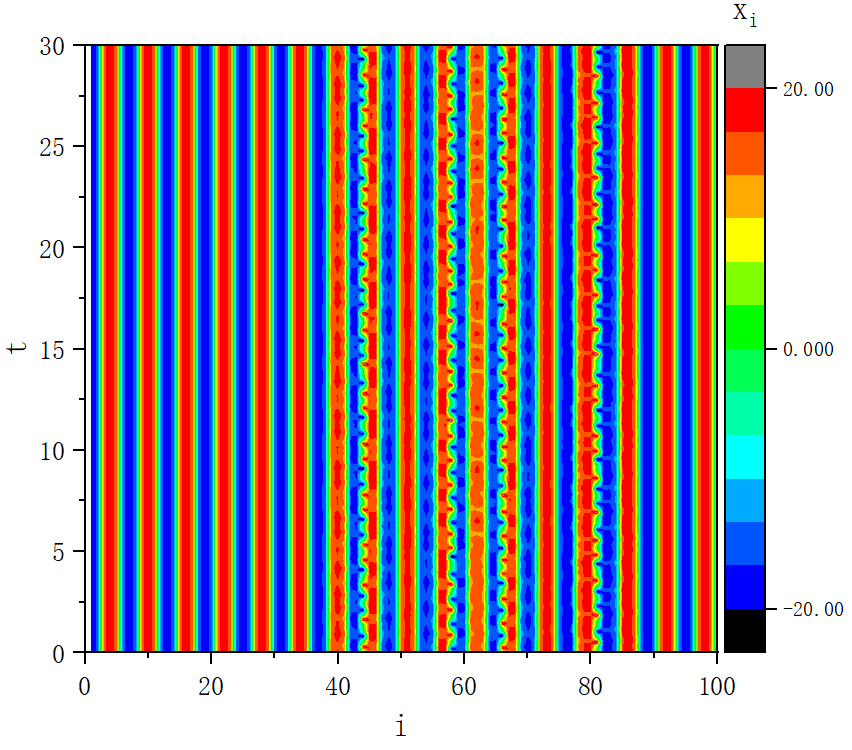
figure 4_D

figure 5

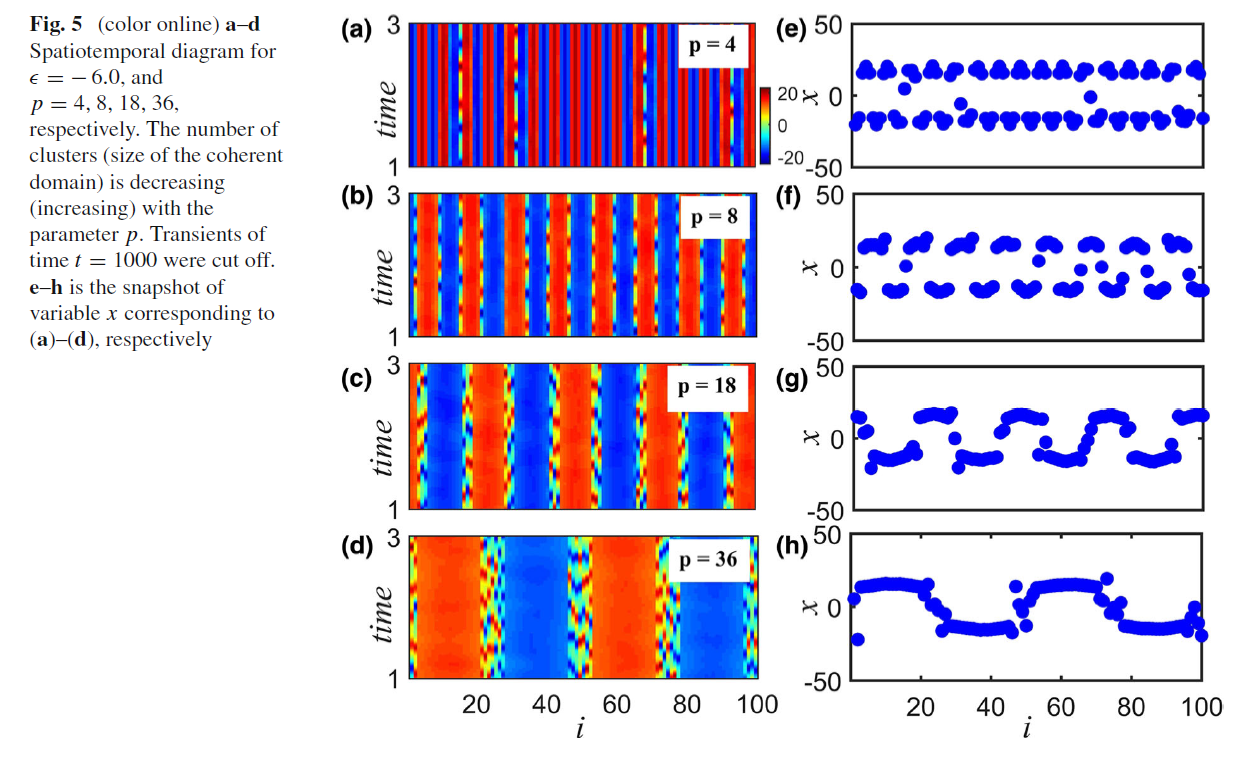
module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=1003000,T_trans=1000000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p=36
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-6.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    max=-10000.0
    min=10000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
            do i=1,M,1
                write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                if(t-1==T_trans) then
                    write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
                if(mod(t,10)==0) then
                    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
            end do
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main

figure 5_A

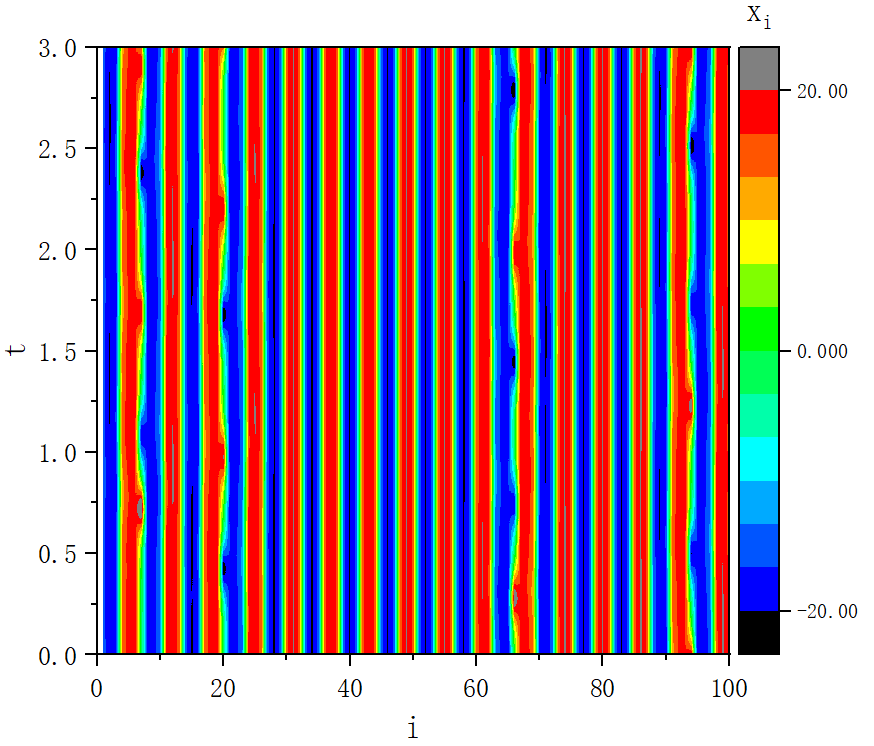
figure 5_B

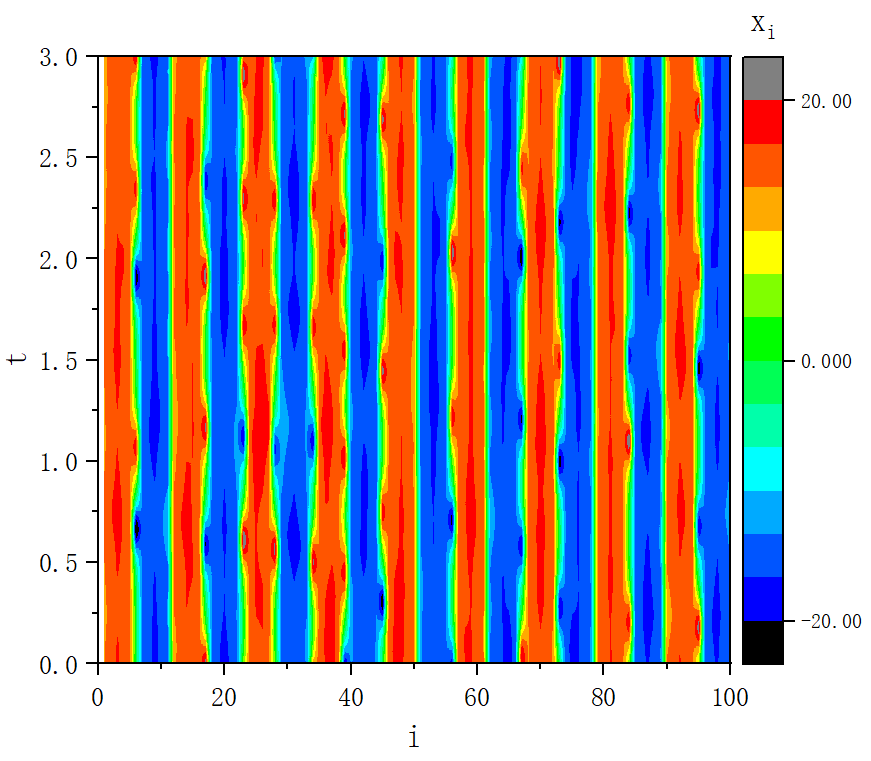
figure 5_C

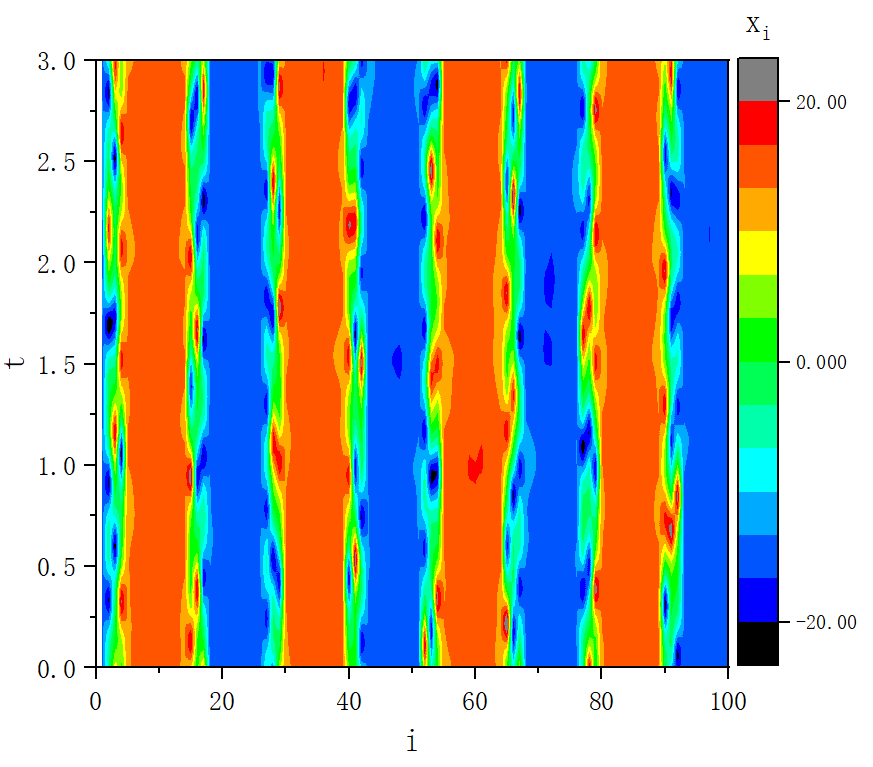
figure 5_D

figure 5_E

figure 5_F

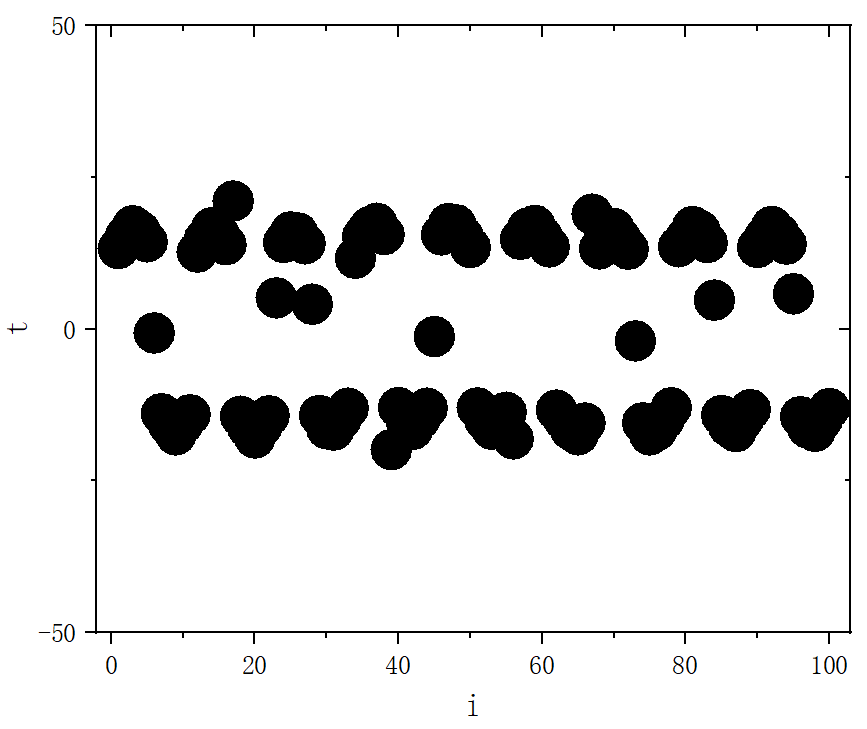
figure 5_G

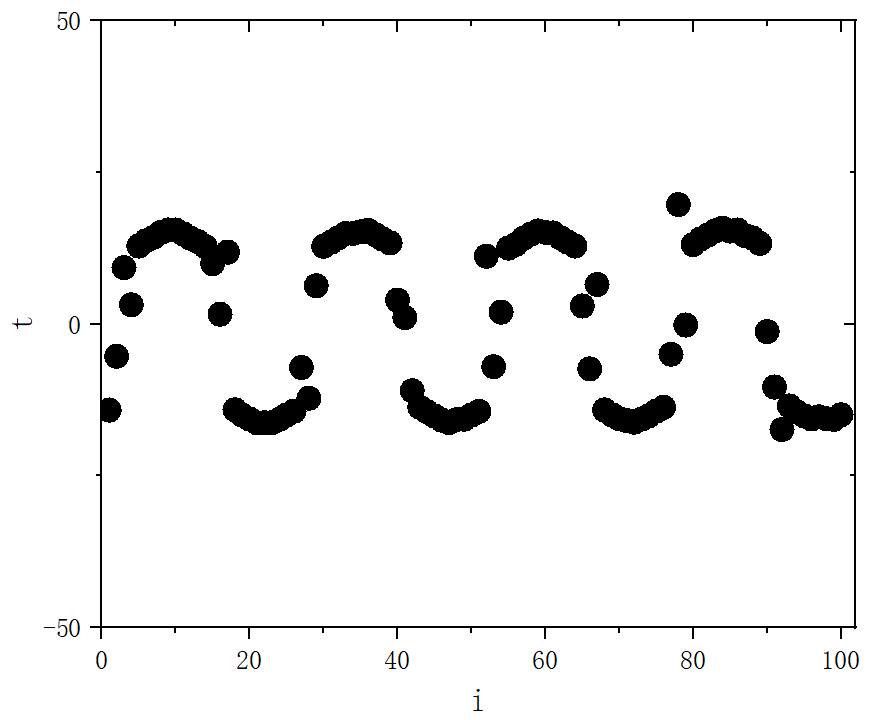
figure 5_H

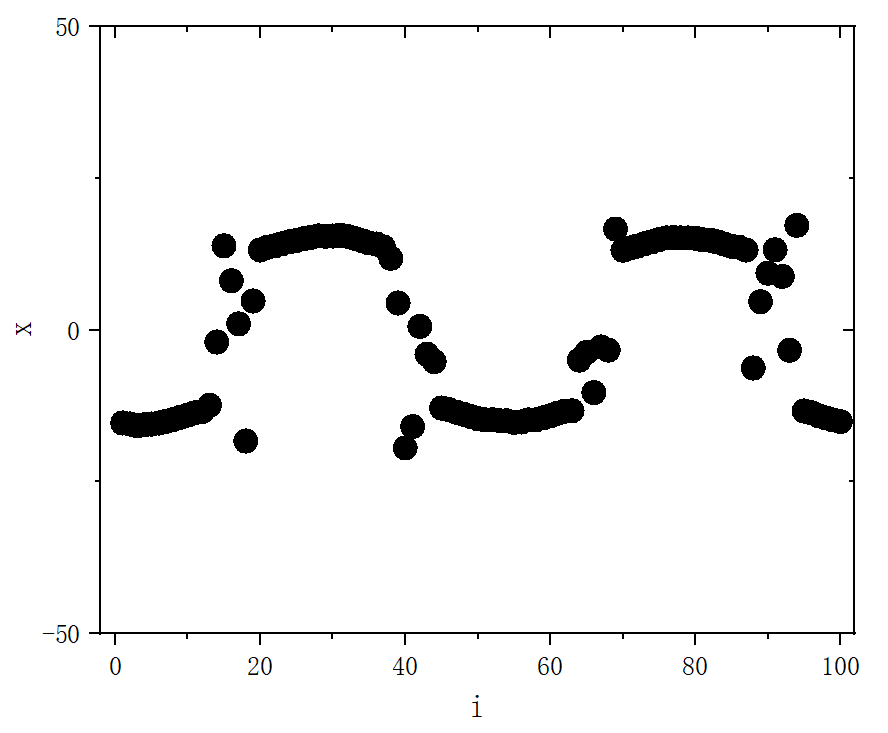
figure 6

module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=1030000,T_trans=1000000,N=3,M=200
    real(kind=8) :: x(M,N)
    integer :: p
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            !write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-6.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
!        do i=1,M,1
!            do j=1,M,1
!                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
!            end do
!            write(10,*)
!        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t,Nc
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    open(90,file="p_Nc.txt")
    do p=1,50,1
        max=-10000.0
        min=10000.0
        Nc=0
        call x0()
        call neighbour(2*p)
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
                call Max_Min(x(:,1),max,min)
!                write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
!                write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
                do i=1,M,1
                    !write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    !if((t-T_trans)*h==20) then
                    !    write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    !end if
                    !if(mod(t,50)==0) then
                    !    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    !end if
                end do
            end if
        end do
        do j=1,M-1,1
            write(30,*) j,max(j),min(j)
            if(((max(j)>0.and.min(j)>0).and.max(j+1)<0).or.((max(j)<0.and.min(j)<0).and.max(j+1)>0)) then
                Nc=Nc+1
            end if
        end do
        write(90,*) p,Nc
        write(*,*) p,Nc
        deallocate(neighbour_matrix)
    end do
end program main

figure 6_A

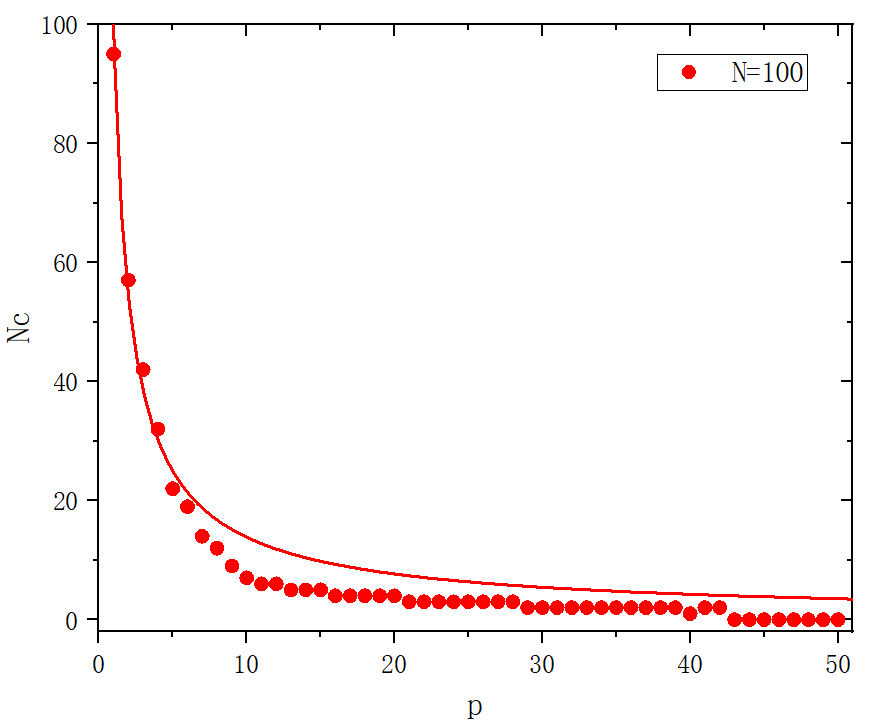
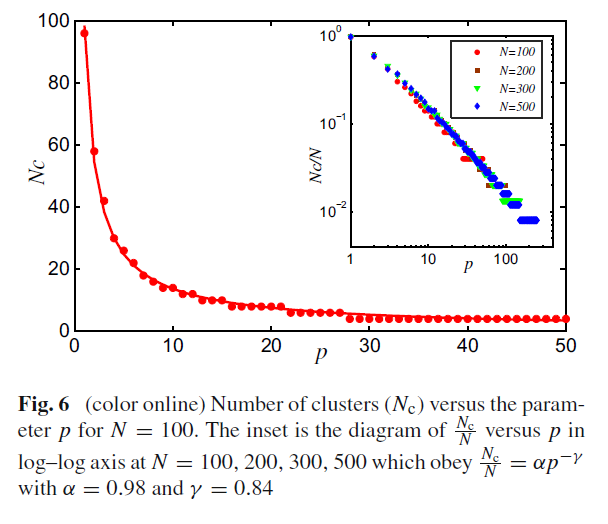
figure 7

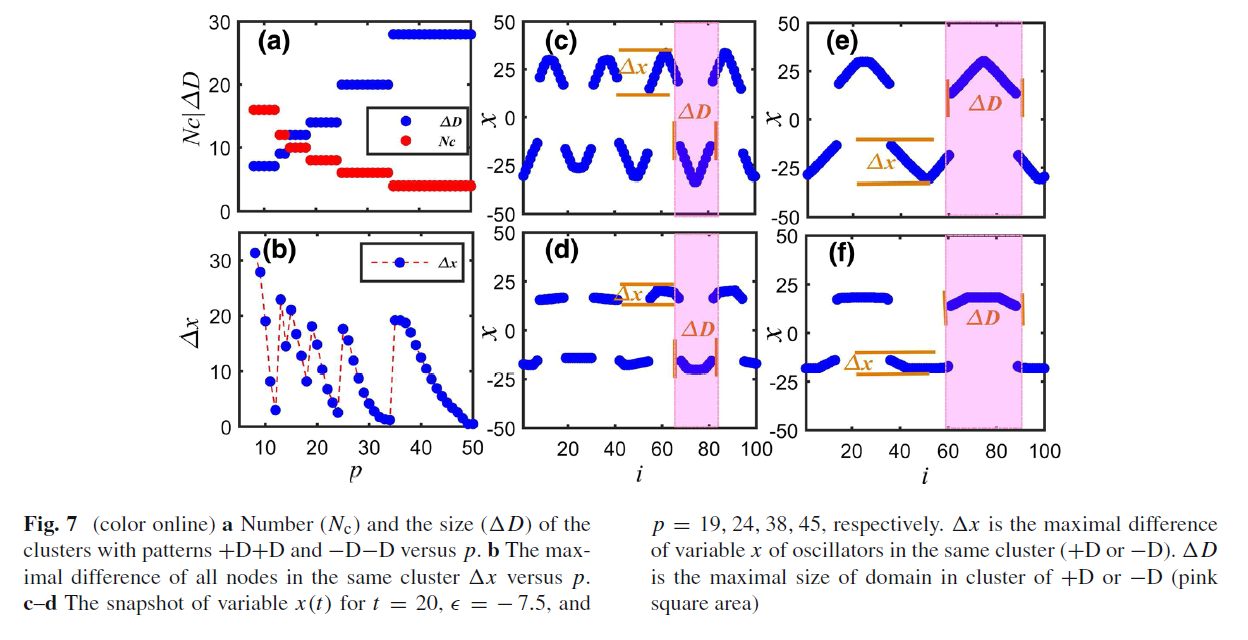
module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=2030000,T_trans=2000000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-7.5
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
!        do i=1,M,1
!            do j=1,M,1
!                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
!            end do
!            write(10,*)
!        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t,Nc
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    open(90,file="p_Nc.txt")
    do p=10,10,1
        max=-10000.0
        min=10000.0
        Nc=0
        call x0()
        call neighbour(2*p)
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
                call Max_Min(x(:,1),max,min)
!                write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
!                write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
                do i=1,M,1
                    write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    if(t-1==T_trans) then
                        write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    end if
                    if(mod(t,50)==0) then
                        write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    end if
                end do
            end if
        end do
        do j=1,M,1
            write(30,*) j,max(j),min(j)
            if((max(j)>0.and.min(j)>0).or.(max(j)<0.and.min(j)<0)) then
                Nc=Nc+1
            end if
        end do
        write(90,*) p,Nc
        write(*,*) p,Nc
        deallocate(neighbour_matrix)
    end do
end program main

figure 7_A

module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=2030000,T_trans=2000000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-7.5
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        !        do i=1,M,1
        !            do j=1,M,1
        !                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
        !            end do
        !            write(10,*)
        !        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t,Nc,count
    real(kind=8) :: max(M),min(M),data_x(M),delta_D(M)
    real,allocatable :: delta_DD(:),delta_DDD(:),delta_X(:)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    open(90,file="p_Nc_deltaD_deltaX.txt")
    do p=7,50,1
        max=-10000.0
        min=10000.0
        data_x=0.0
        delta_D=0.0
        count=1
        Nc=0
        call x0()
        call neighbour(2*p)
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
                call Max_Min(x(:,1),max,min)
                do i=1,M,1
                    if((t-T_trans)*h==20) then
                        data_x(i)=x(i,1)
!                        write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                    end if
                end do
            end if
        end do
        do j=1,M-1,1
            write(30,*) j,max(j),min(j)
            if(((max(j)>0.and.min(j)>0).and.max(j+1)<0).or.((max(j)<0.and.min(j)<0).and.max(j+1)>0)) then
                delta_D(j)=j
                Nc=Nc+1
            end if
        end do
        allocate(delta_DD(Nc))
        allocate(delta_DDD(Nc))
        allocate(delta_X(Nc))
        delta_DD=0.0
        delta_DDD=0.0
        delta_X=0.0
        do j=1,M,1
            if(delta_D(j)>0.0) then
                delta_DD(count)=delta_D(j)
                count=count+1
            end if
        end do
        do j=1,Nc-1,1
            delta_DDD(j)=abs(delta_DD(j+1)-delta_DD(j))
            delta_X(j)=abs(maxval(data_x(delta_DD(j)+1:delta_DD(j+1)))-minval(data_x(delta_DD(j)+1:delta_DD(j+1))))
        end do
        write(*,*) p,Nc,"delta_X",maxval(delta_X(:)),"delta_DDD",maxval(delta_DDD(:))
        write(90,*) p,Nc,maxval(delta_X(:)),maxval(delta_DDD(:))
        deallocate(neighbour_matrix)
        deallocate(delta_DD)
        deallocate(delta_DDD)
        deallocate(delta_X)
    end do
end program main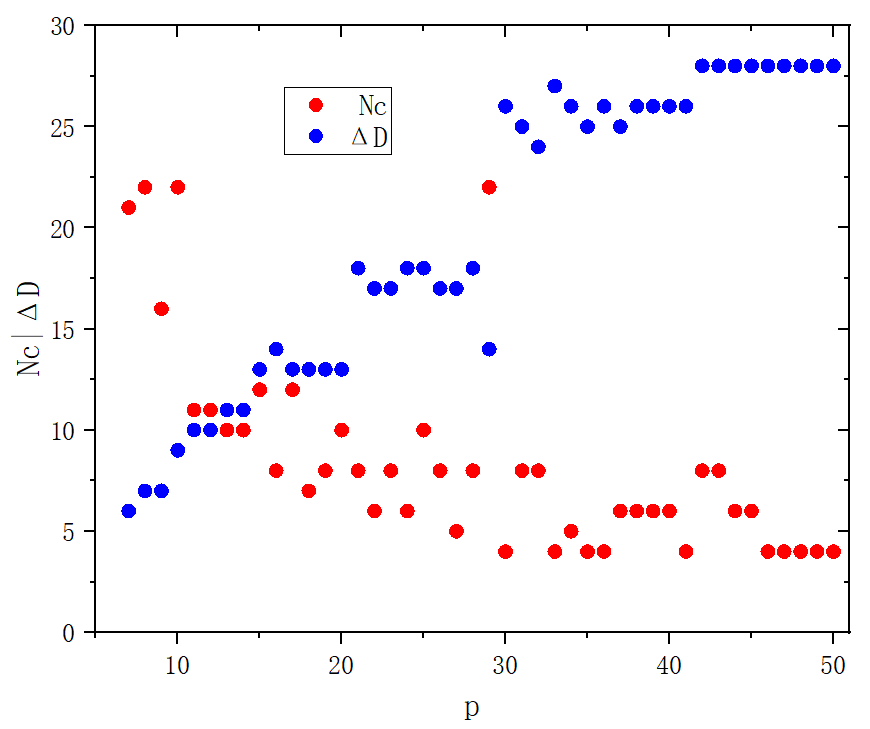

figure 7_B

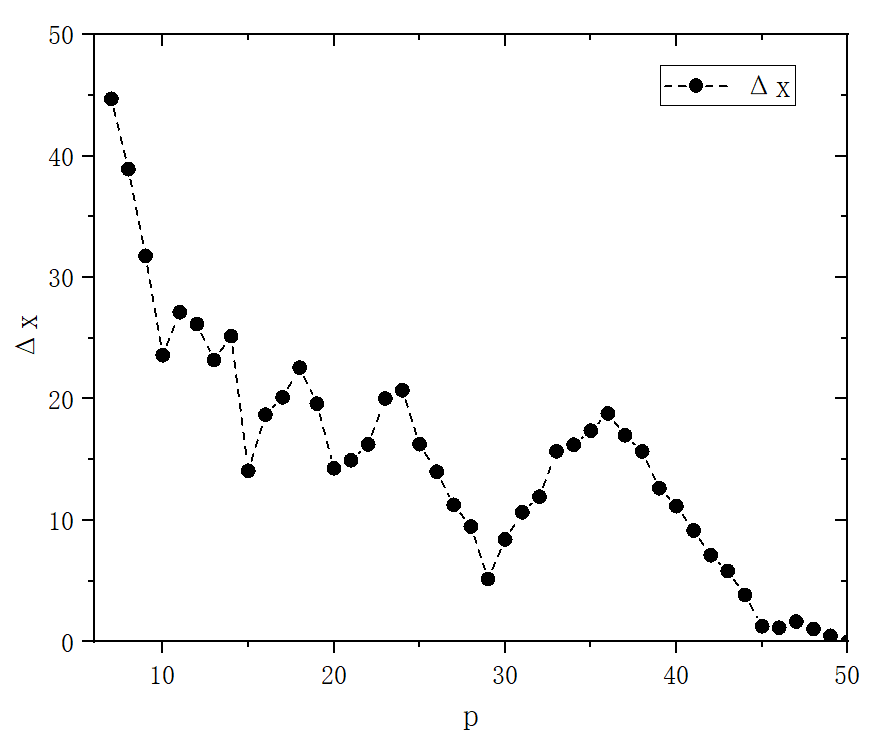
figure 7_C

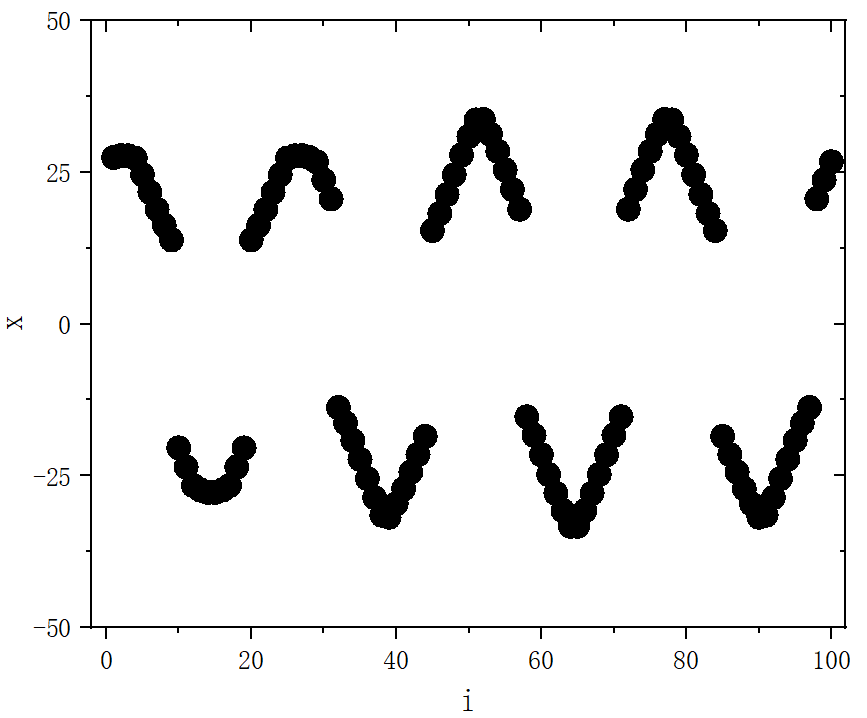
figure 7_D

• p=28

figure 7_E

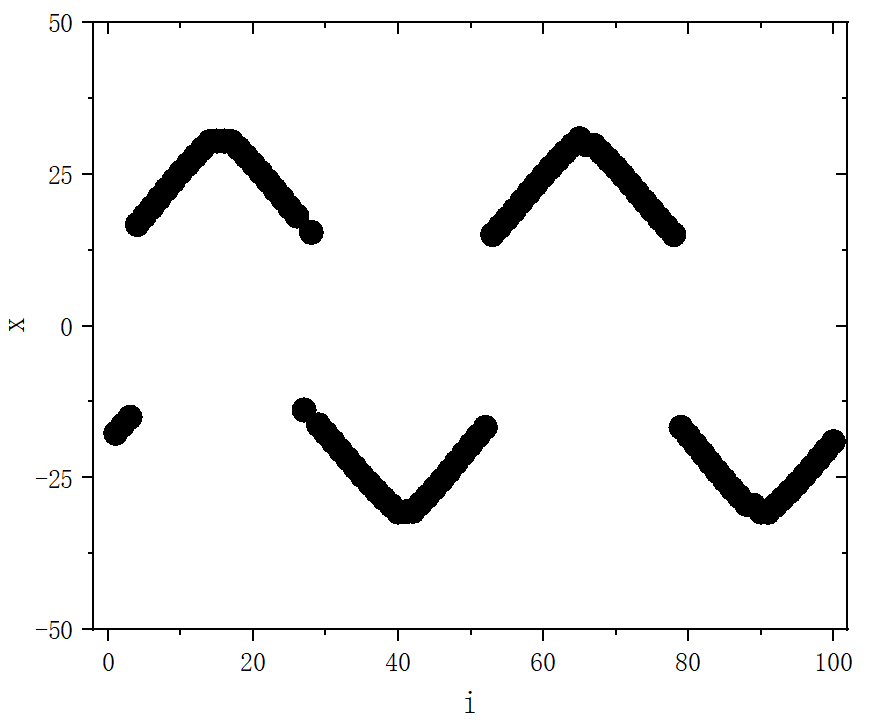
figure 7_F

• p=44

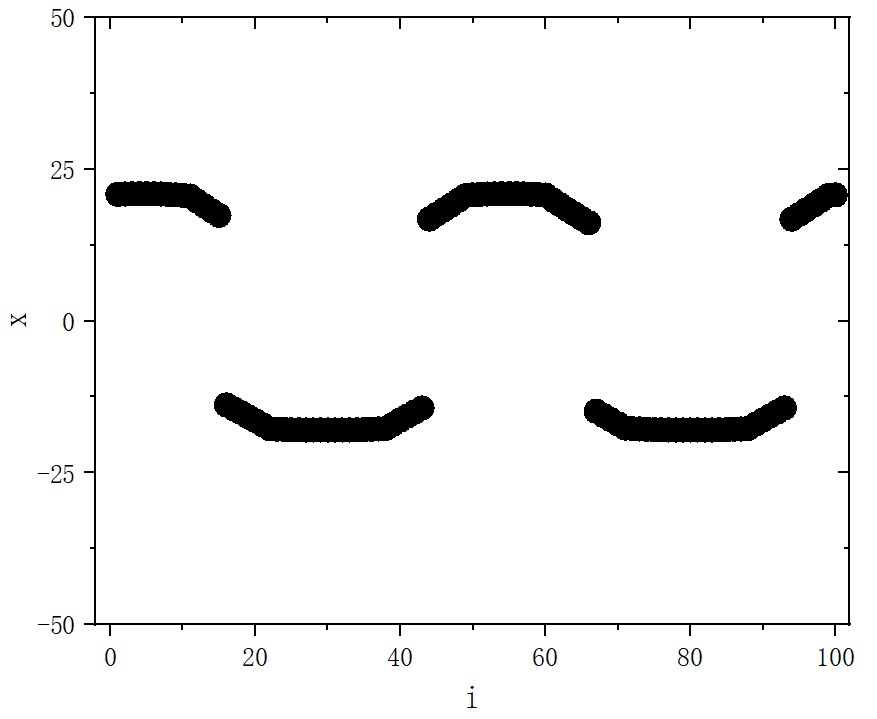
figure 8

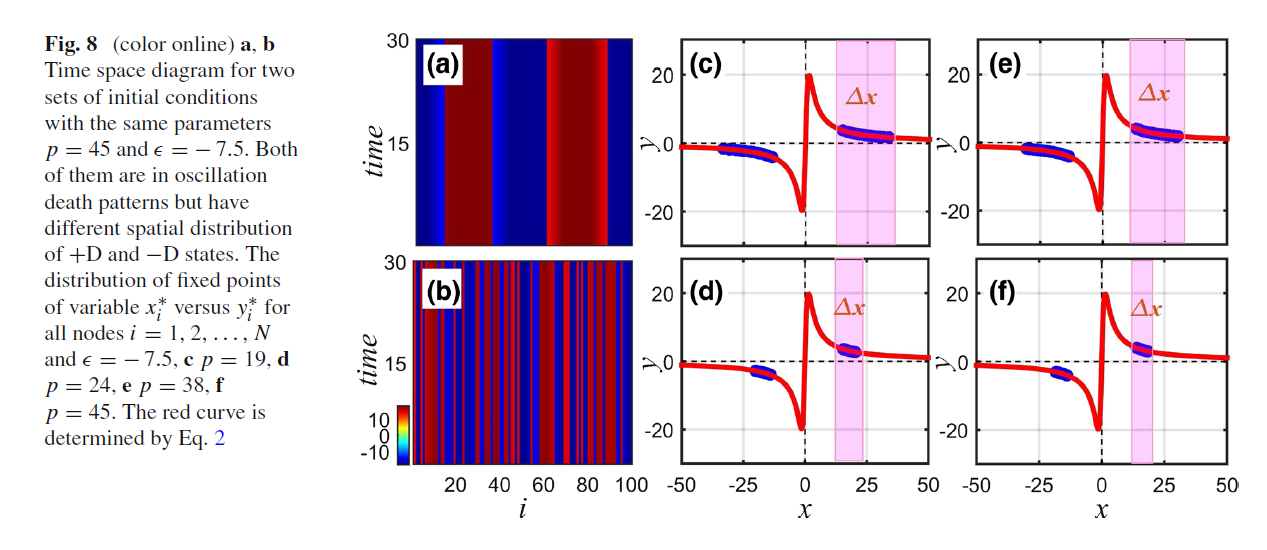
figure 8_A

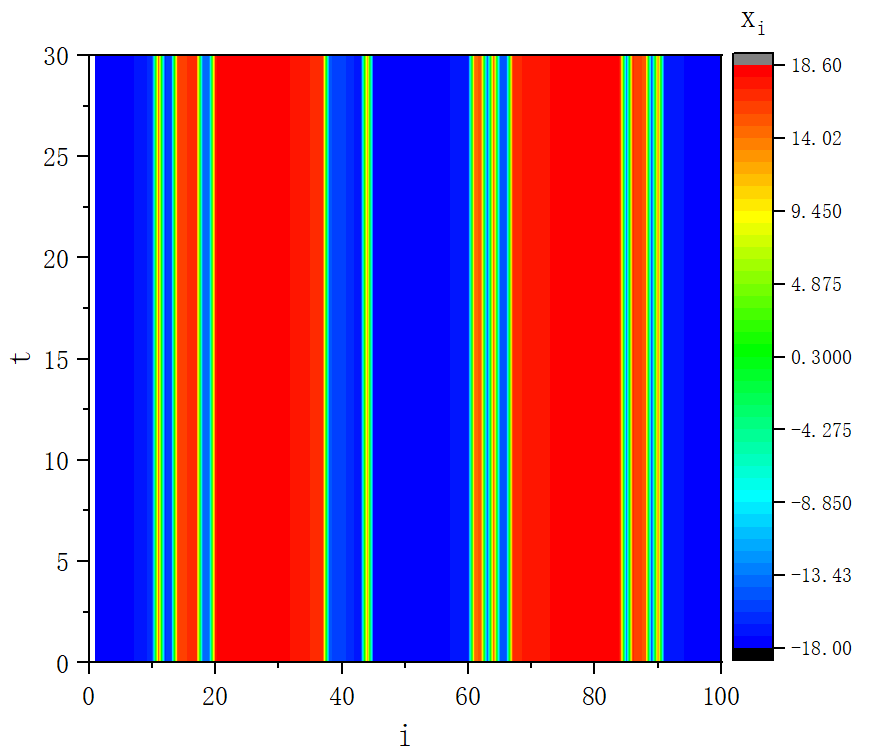
figure 8_B

figure 8_C

figure 8_D

p=28

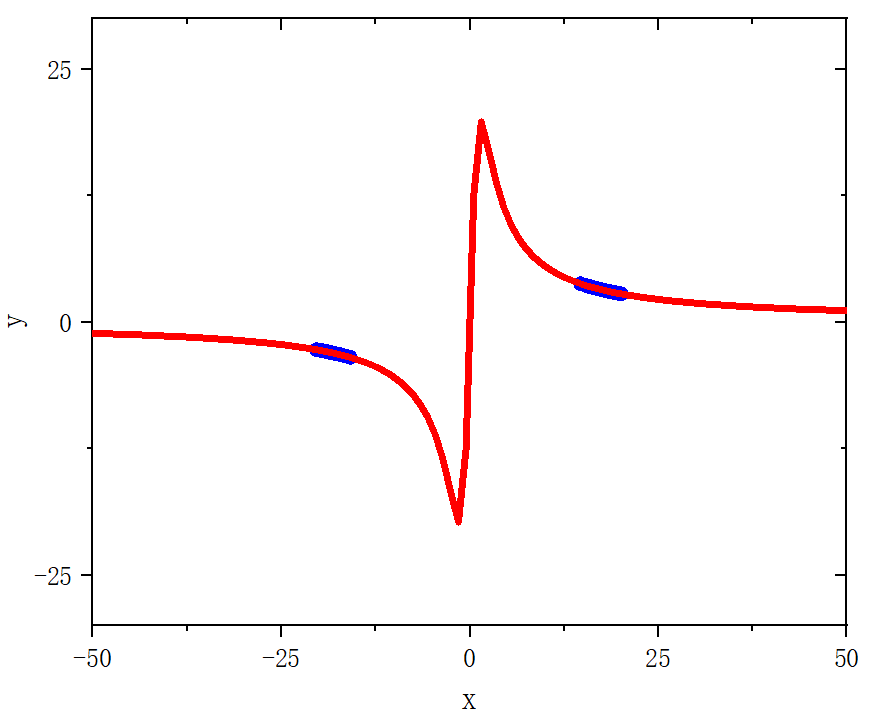
figure 8_E

figure 8_F

• p=44

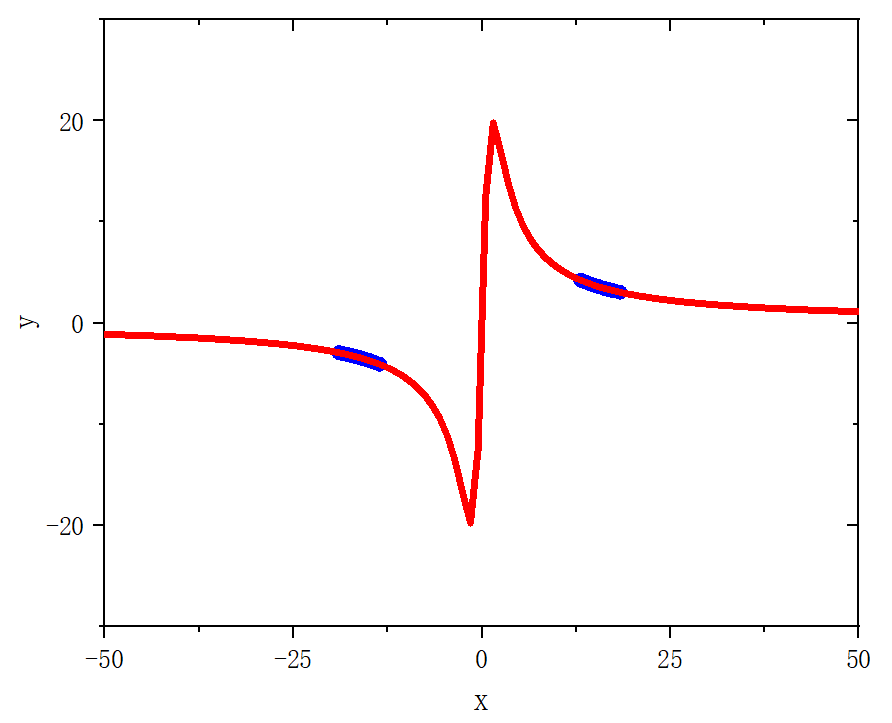
figure 9

• 时空斑图

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=200300,T_trans=200000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p=35
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=31.0*x1-14.0
            x(i,2)=44.0*x2-20.0
            x(i,3)=23.0*x3-1.0
            write(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-5.5
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    max=-10000.0
    min=10000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
            do i=1,M,1
                write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                if(t-1==T_trans) then
                    write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
                if(mod(t,50)==0) then
                    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
            end do
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main

• SI

module Lorenz
    implicit none
    real,parameter :: h=0.001
    integer,parameter :: MaxT=230000,T_trans=200000,N=3,M=100,mm=50
    real(kind=8) :: x(M,N),epsilon
    integer :: p=35
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
!            call random_number(x1)
!            call random_number(x2)
!            call random_number(x3)
!            x(i,1)=31.0*x1-14.0
!            x(i,2)=44.0*x2-20.0
!            x(i,3)=23.0*x3-1.0
            read(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling
        coupling=0.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !SI不相干强度
    subroutine SIM(Z)
        implicit none
        integer :: i,j,t,nn
        real(kind=8) :: delta
        real(kind=8) :: Z(M,MaxT-T_trans),sigma(mm),S(mm),ZZm(M,MaxT-T_trans),ZZ(MaxT-T_trans)
        real(kind=8) :: Sm,SI
        delta=1.0
        SI=0.0
        ZZm=0.0
        ZZ=0.0
        nn=M/mm
        do i=1,M-1,1
            do t=1,MaxT-T_trans,1
                ZZm(i,t)=Z(i,t)-Z(i+1,t)
            end do
        end do
        do t=1,MaxT-T_trans,1
            ZZ(t)=sum(ZZm(:,t))/real(M-1)
        end do
        sigma=0.0
        do j=1,m,1
            do i=nn*(j-1)+1,nn*j,1
                do t=1,MaxT-T_trans,1
                    sigma(j)=sigma(j)+(ZZm(i,t)-ZZ(t))**2
                end do
            end do
            sigma(j)=sqrt(sigma(j)/real(nn))/((MaxT-T_trans)*h)
        end do

        do j=1,mm,1
            Sm=sigma(j)-delta
            if(Sm>0.0) then
                S(j)=1.0
            else
                S(j)=0.0
            end if
        end do
        SI=sum(S(:))/real(mm)
        write(100,*) epsilon,SI
        write(*,*) epsilon,SI
        return
    end subroutine SIM

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        !        do i=1,M,1
        !            do j=1,M,1
        !                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
        !            end do
        !            write(10,*)
        !        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t,Nc,count
    real(kind=8) :: max(M),min(M),data_x(M),delta_D(M),Z(M,MaxT-T_trans)
!    real,allocatable :: delta_DD(:),delta_DDD(:),delta_X(:)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    open(90,file="p_Nc_deltaD_deltaX.txt")
    open(100,file="epsilon_SI.txt")
    call x0()
    call neighbour(2*p)
    do epsilon=-5.0,-7.5,-0.1
        max=-10000.0
        min=10000.0
        data_x=0.0
        delta_D=0.0
        count=1
        Nc=0
        Z=0.0
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
!                call Max_Min(x(:,1),max,min)
                Z(:,t-T_trans)=x(:,3)
!                do i=1,M,1
!                    write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
!                    if(t-1==T_trans) then
!                        data_x(i)=x(i,1)
!                        write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
!                    end if
!                    if(mod(t,50)==0) then
!                        write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
!                    end if
!                end do
            end if
        end do
        call SIM(Z)
!        do j=1,M-1,1
!            write(30,*) j,max(j),min(j)
!            if(((max(j)>0.and.min(j)>0).and.max(j+1)<0).or.((max(j)<0.and.min(j)<0).and.max(j+1)>0)) then
!                delta_D(j)=j
!                Nc=Nc+1
!            end if
!        end do
!        allocate(delta_DD(Nc))
!        allocate(delta_DDD(Nc))
!        allocate(delta_X(Nc))
!        delta_DD=0.0
!        delta_DDD=0.0
!        delta_X=0.0
!        do j=1,M,1
!            if(delta_D(j)>0.0) then
!                delta_DD(count)=delta_D(j)
!                count=count+1
!            end if
!        end do
!        do j=1,Nc-1,1
!            delta_DDD(j)=abs(delta_DD(j+1)-delta_DD(j))
!            delta_X(j)=abs(maxval(data_x(delta_DD(j)+1:delta_DD(j+1)))-minval(data_x(delta_DD(j)+1:delta_DD(j+1))))
!        end do
!        write(*,*) p,Nc,"delta_X",maxval(delta_X(:)),"delta_DDD",maxval(delta_DDD(:))
!        write(90,*) p,Nc,maxval(delta_X(:)),maxval(delta_DDD(:))
!        deallocate(delta_DD)
!        deallocate(delta_DDD)
!        deallocate(delta_X)
    end do
    deallocate(neighbour_matrix)
end program main

figure 9_A

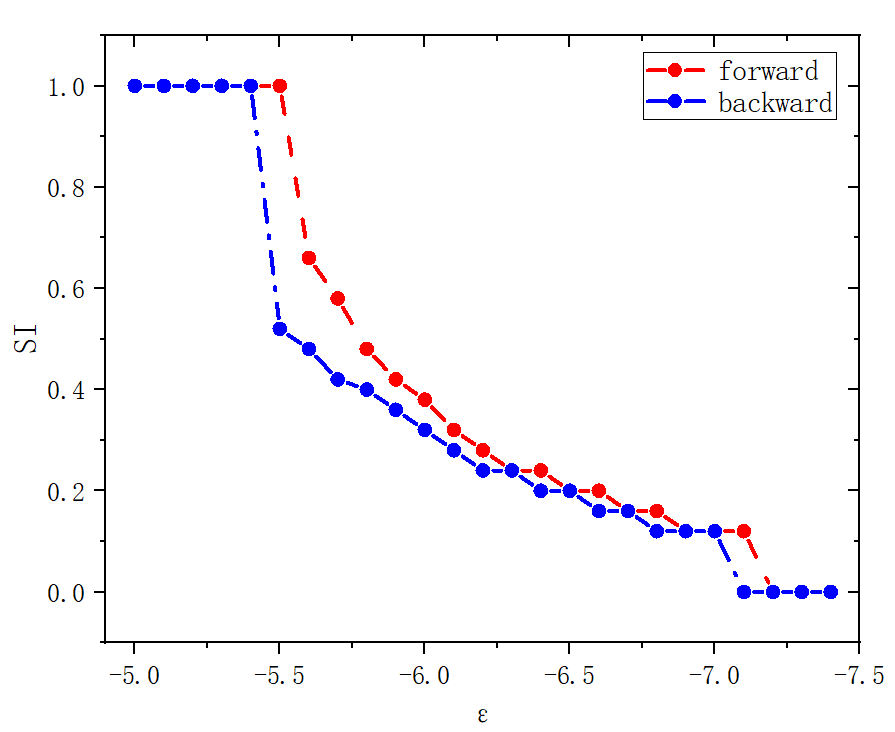
figure 9_B

figure 9_C

figure 9_D

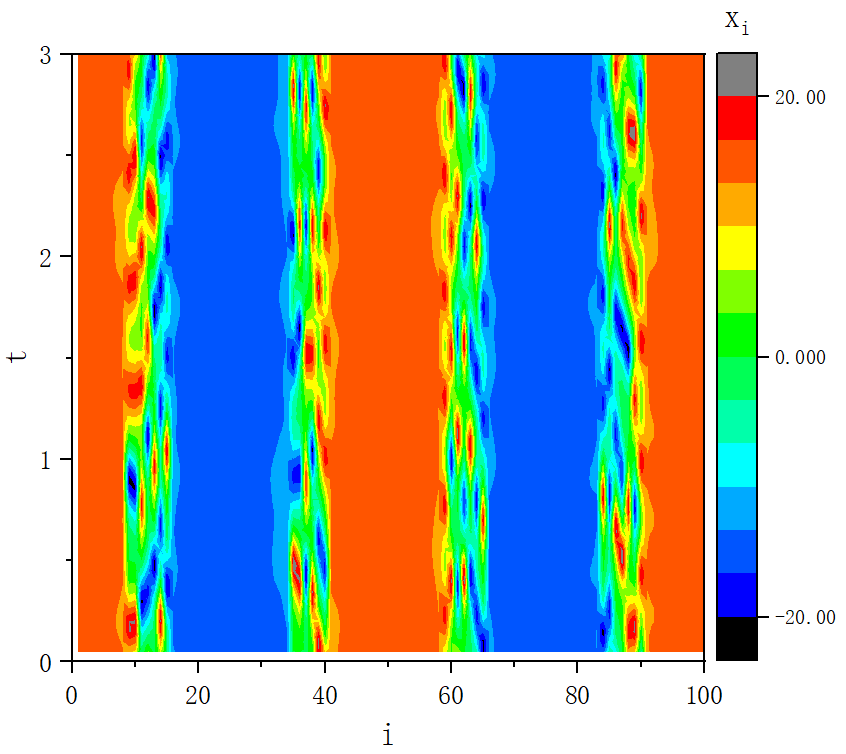
figure 9_E

figure 9_F

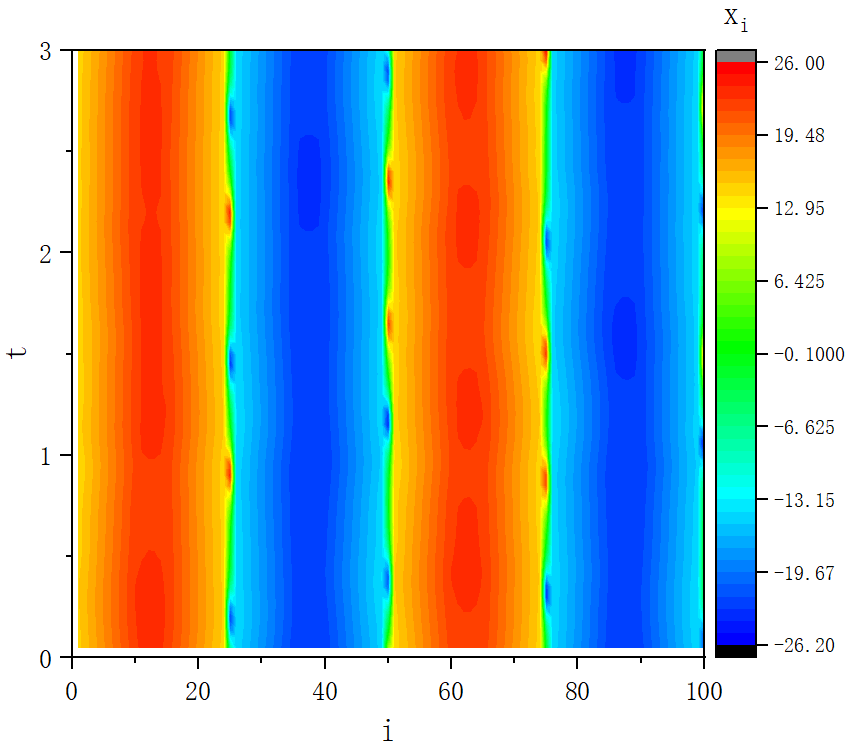
figure 9_G

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=200300,T_trans=200000,N=3,M=100
    real(kind=8) :: x(M,N)
    integer :: p=35
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        do i=1,M,1
            !call random_number(x1)
            !call random_number(x2)
            !call random_number(x3)
            !x(i,1)=31.0*x1-14.0
            !x(i,2)=44.0*x2-20.0
            !x(i,3)=23.0*x3-1.0
            read(20,*) x(i,1),x(i,2),x(i,3)
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,j,i
        real(kind=8) :: a,b,c,coupling,epsilon
        coupling=0.0
        epsilon=-7.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,1)-x(i,1))
        end do
        a=10.0
        b=2.0
        c=28.0
        fx(1)=a*(xx(2)-xx(1))+(epsilon/real(2.0*p))*coupling
        fx(2)=c*xx(1)-xx(1)*xx(3)-xx(2)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,j,t
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !max与min
    subroutine Max_Min(xxx,max,min)
        implicit none
        real(kind=8) :: max(M),min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(max(i)<xxx(i)) then
                max(i)=xxx(i)
            end if
            if(min(i)>xxx(i)) then
                min(i)=xxx(i)
            end if
        end do
        return
    end subroutine Max_Min

    !建立网络矩阵
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                if(abs(i-j)<=K/2.or.abs(i-j)>=M-K/2) then
                    neighbour_matrix(i,j)=1
                    neighbour_matrix(j,i)=1
                end if
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: i,j,t
    real(kind=8) :: max(M),min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="x0.txt")
    open(30,file="c_M_max_min.txt")
    open(40,file="t_x_y_z_14.txt")
    open(50,file="t_x_y_z_15.txt")
    open(60,file="i_t_x_y_z.txt")
    open(70,file="i_t_x_y_z_kuaizhao.txt")
    open(80,file="i_t_x_y_z_all.txt")
    max=-10000.0
    min=10000.0
    call x0()
    call neighbour(2*p)
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call Max_Min(x(:,1),max,min)
            write(40,"(4(F15.6))") (t-T_trans)*h,x(14,1),x(14,2),x(14,3)
            write(50,"(4(F15.6))") (t-T_trans)*h,x(15,1),x(15,2),x(15,3)
            do i=1,M,1
                write(80,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                if(t-1==T_trans) then
                    write(70,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
                if(mod(t,50)==0) then
                    write(60,"(5(F15.6))") real(i),(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
                end if
            end do
        end if
    end do
    do j=1,M,1
        write(30,*) j,max(j),min(j)
    end do
end program main