通过诱导多稳奇异态的出现

Emergence of chimeras through induced multistability

阅读

下载地址：

2018_PRE_Emergence of chimeras through induced multistability.pdf

复现

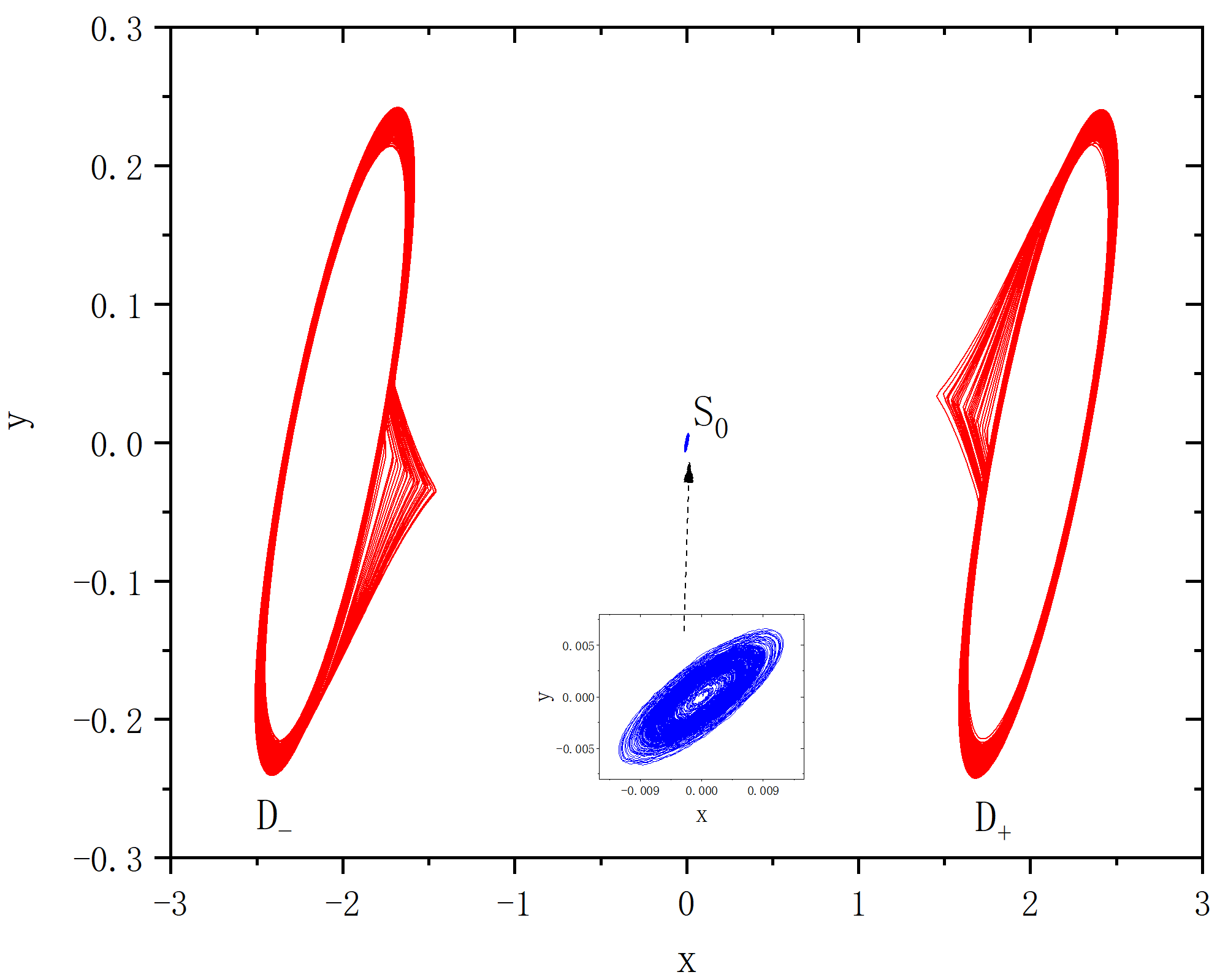
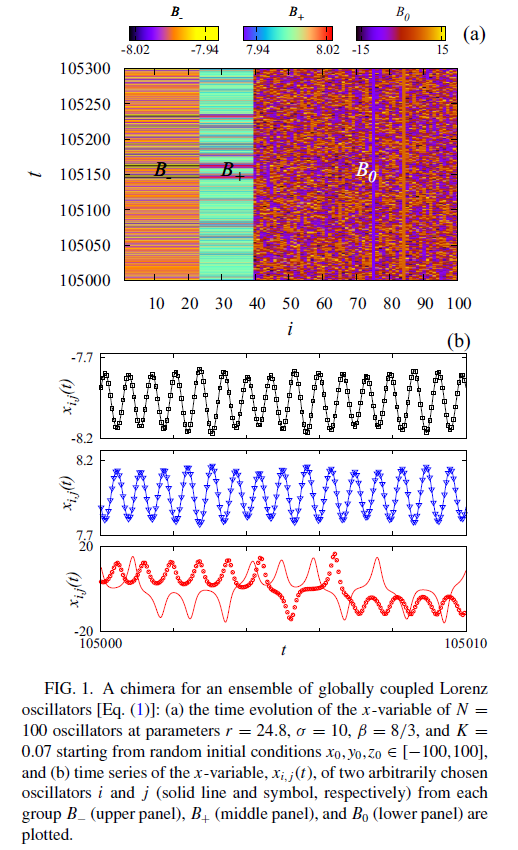
figure 1

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=10530000,T_trans=10500000,N=3,M=100
    real :: x(M,N)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            !call random_number(x1)
            !call random_number(x2)
            !call random_number(x3)
            !x(i,1)=x1*100.0-100.0
            !x(i,2)=x2*100.0-100.0
            !x(i,3)=x3*100.0-100.0
            read(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real :: xx(N),fx(N),coupling
        integer :: t,i,j
        real :: a,b,c,K
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=24.8 !r
        K=0.07
        coupling=0.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
        end do
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)+(K/real(M-1))*coupling
        return
    end subroutine fnf


    subroutine rk4(x)
        implicit none
        integer :: i
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour(K)
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour


end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j,p=1,counter
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_5.txt")
    open(42,file="t_x_50.txt")
    open(43,file="t_x_23.txt")
    open(44,file="t_x_95.txt")
    open(45,file="t_x_36.txt")
    open(46,file="t_x_61.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="error.txt")
    call neighbour(2*p)
    call x0
    U_max=-1000.0
    U_min=1000.0
    counter=1
    do t=1,MaxT,1
        call rk4(x)
        if(t>T_trans) then
            call U_max_min(x(:,1),U_max,U_min)
            write(40,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(41,*) (t-T_trans)*h,x(5,1),x(5,2),x(5,3)
            write(42,*) (t-T_trans)*h,x(50,1),x(50,2),x(50,3)
            write(43,*) (t-T_trans)*h,x(23,1),x(23,2),x(23,3)
            write(44,*) (t-T_trans)*h,x(95,1),x(95,2),x(95,3)
            write(45,*) (t-T_trans)*h,x(36,1),x(36,2),x(36,3)
            write(46,*) (t-T_trans)*h,x(61,1),x(61,2),x(61,3)
            !将相同的动力学模式放在一起
            do i=1,M,1
                data(i,t-T_trans,1) = x(i,1)
                data(i,t-T_trans,2) = x(i,2)
                data(i,t-T_trans,3) = x(i,3)
            end do
        end if
    end do
    do i=1,M,1
        write(30,*) i,U_max(i),U_min(i)
        do t=1,MaxT-T_trans,1
            if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_max(i)<0) then
                !B-
                if(mod(t,100)==0) then
                    write(20,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_min(i)>0) then
                !B+
                if(mod(t,100)==0) then
                    write(21,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)-U_min(i)>5.0.and.U_min(i)<0.and.U_max(i)>0) then
                !B0
                if(mod(t,100)==0) then
                    write(22,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else
                write(60,*) "条件有误！"
            end if
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
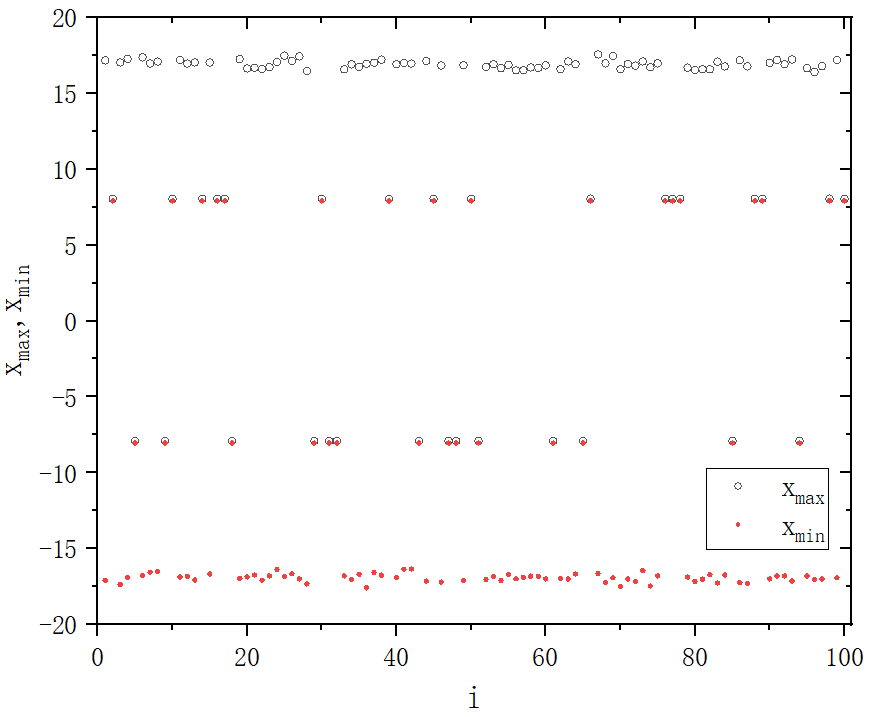
end program main

figure 1_A

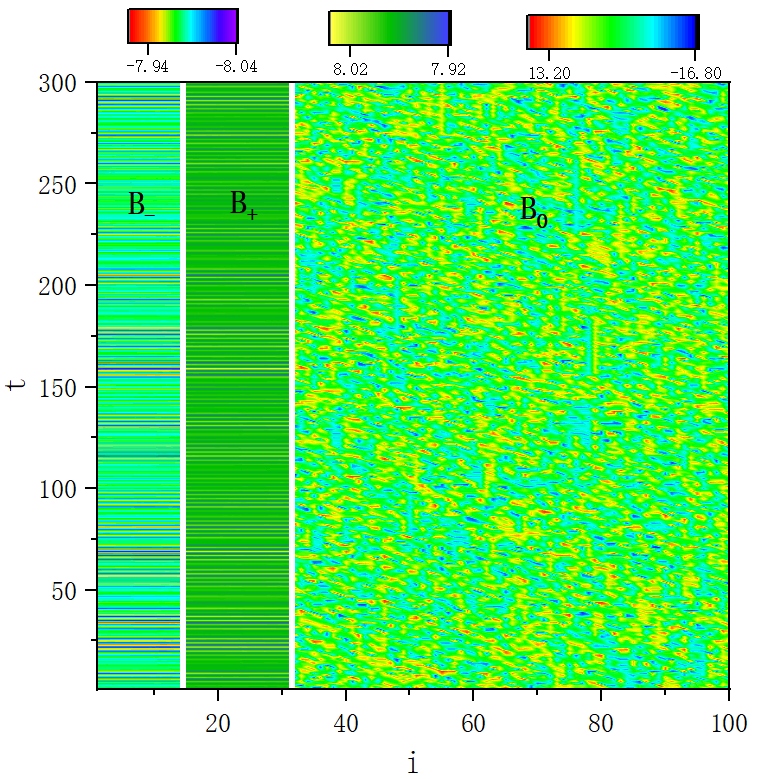
figure 1_B

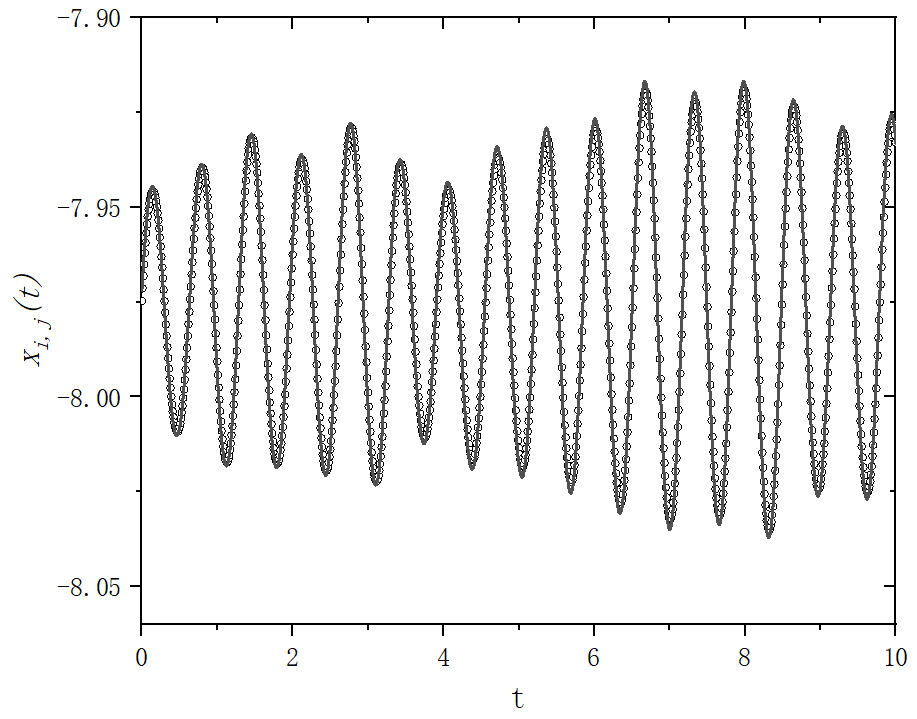
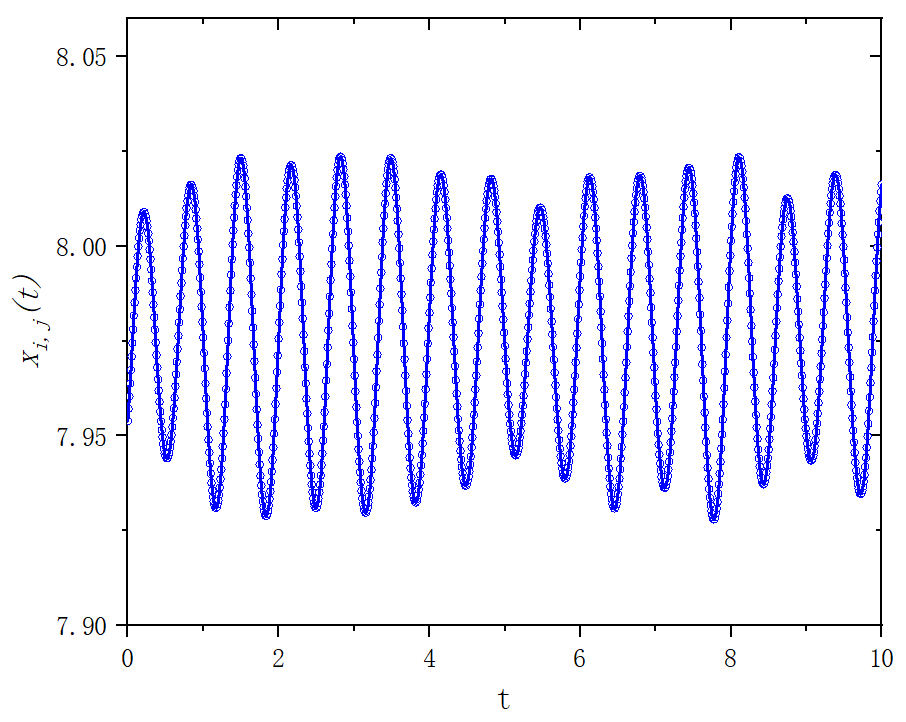
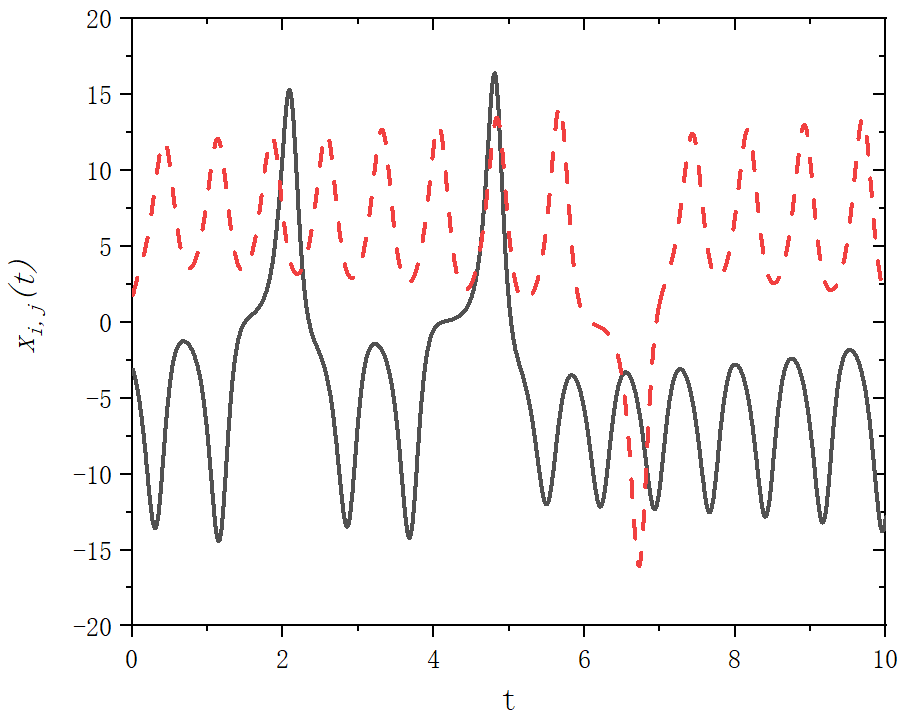
figure 2

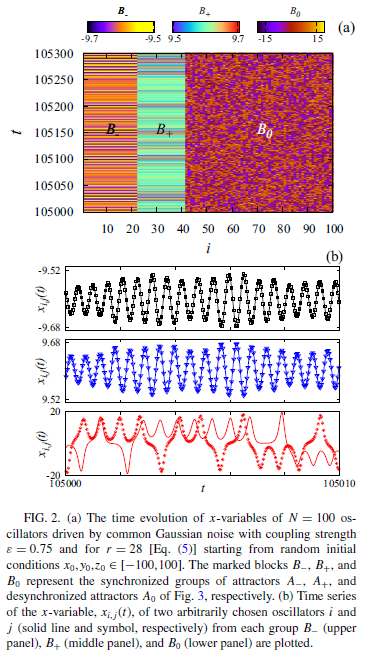
module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=180000,T_trans=150000,N=3,M=100
    real :: x(M,N),f(MaxT)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            !call random_number(x1)
            !call random_number(x2)
            !call random_number(x3)
            !x(i,1)=x1*100.0-100.0
            !x(i,2)=x2*100.0-100.0
            !x(i,3)=x3*100.0-100.0
            read(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i,t)
        implicit none
        real :: xx(N),fx(N)
        integer :: t,i,j
        real :: a,b,c,K,epsilon
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=28.0 !r
        epsilon=0.75
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)+epsilon*(f(t)-xx(3))
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0          ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            !write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise


end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    call neighbour()
    call x0
    call gaussNoise()
    U_max=-1000.0
    U_min=1000.0
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call U_max_min(x(:,1),U_max,U_min)
            write(40,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(41,*) (t-T_trans)*h,x(4,1),x(4,2),x(4,3)
            write(42,*) (t-T_trans)*h,x(8,1),x(8,2),x(8,3)
            write(43,*) (t-T_trans)*h,x(17,1),x(17,2),x(17,3)
            write(44,*) (t-T_trans)*h,x(29,1),x(29,2),x(29,3)
            write(45,*) (t-T_trans)*h,x(20,1),x(20,2),x(20,3)
            write(46,*) (t-T_trans)*h,x(26,1),x(26,2),x(26,3)
            !将相同的动力学模式放在一起
            do i=1,M,1
                data(i,t-T_trans,1) = x(i,1)
                data(i,t-T_trans,2) = x(i,2)
                data(i,t-T_trans,3) = x(i,3)
            end do
        end if
    end do
    do i=1,M,1
        write(30,*) i,U_max(i),U_min(i)
                do t=1,MaxT-T_trans,1
            if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_max(i)<0) then
                !B-
                if(mod(t,100)==0) then
                    write(20,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_min(i)>0) then
                !B+
                if(mod(t,100)==0) then
                    write(21,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)-U_min(i)>5.0.and.U_min(i)<0.and.U_max(i)>0) then
                !B0
                if(mod(t,100)==0) then
                    write(22,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else
                write(60,*) "条件有误！"
            end if
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main

figure 2_A

module Tools
    implicit none
    integer :: Rows
    real,allocatable :: c_peak_interval(:,:)
contains
    !确定文件行数
    subroutine read_file()
        implicit none
        integer :: count,iostat,number,i,j
        real :: x1,x2,x3,x4,x5
        character(len=100) :: line ! 用于存储每行数据
        ! 打开文件
        open(unit=5, file='i_t_x_B0.txt', status='old', action='read')
        ! 逐行读取文件并计算行数
        count = 0
        number= 300
        do
            read(5, '(A)', iostat=iostat) line
            if (iostat /= 0) exit ! 如果读取到文件末尾，则退出循环
            count = count + 1
        end do
        Rows=count
        close(5)
        open(unit=5, file='i_t_x_B0.txt', status='old', action='read')
        do i=1,Rows/number,1
            do j=1,number,1
                read(5,*) x1,x2,x3,x4,x5
                write(10,*) i,x2,x3,x4,x5
            end do
        end do

    end subroutine read_file

end module Tools



program main
    use Tools
    implicit none
    open(10,file="i_t_x_B0_modify.txt")
    call read_file
    return
end program main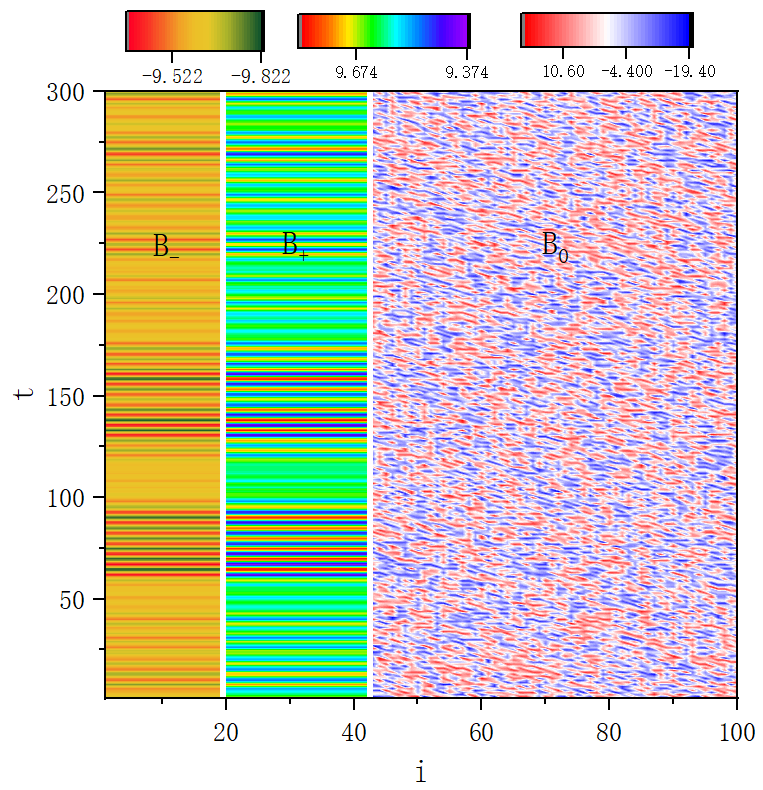

figure 2_B

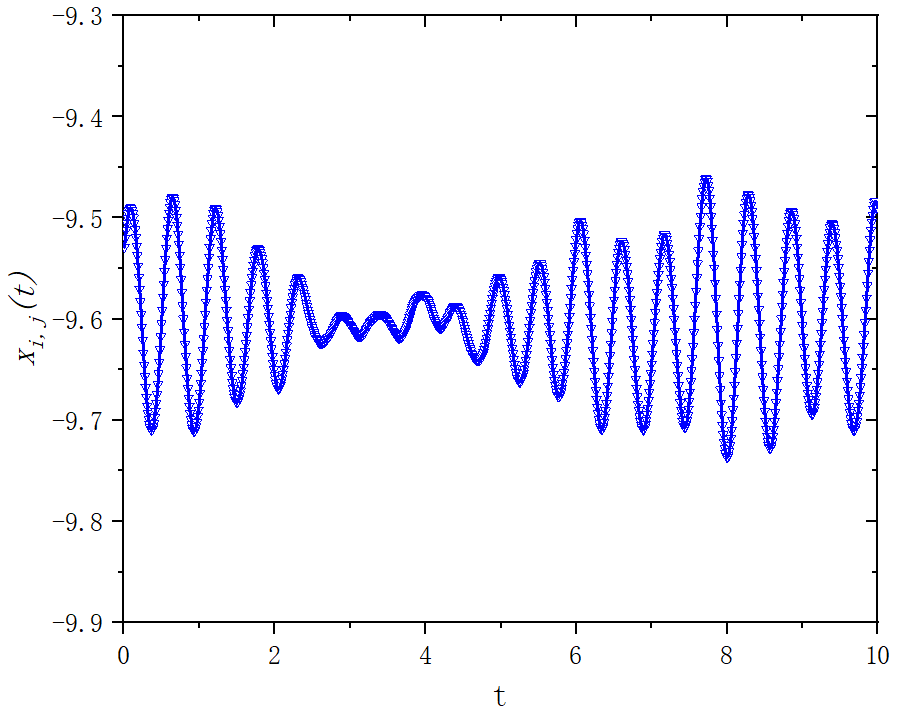
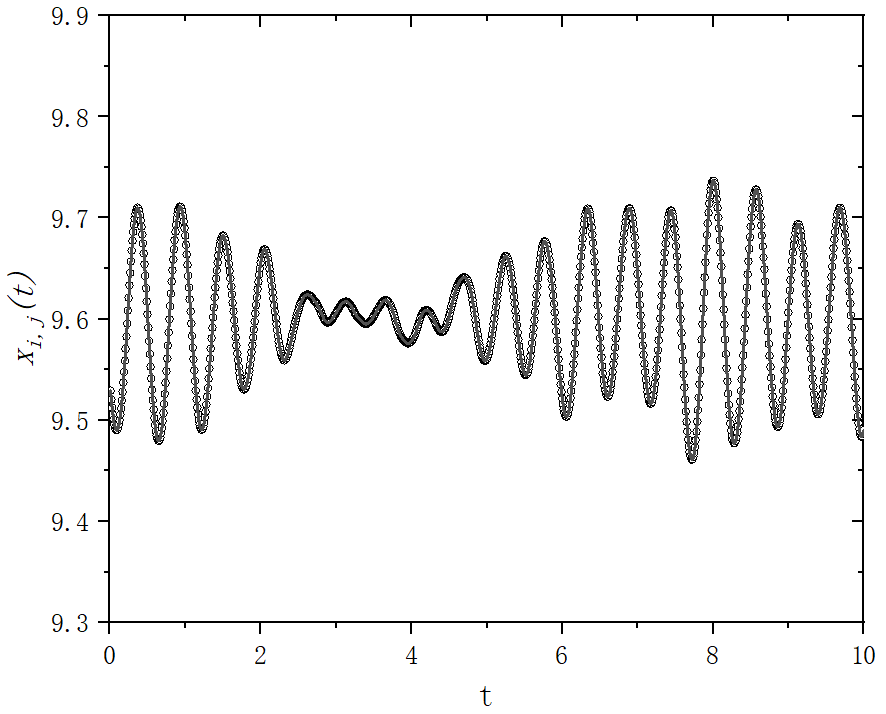
figure 3

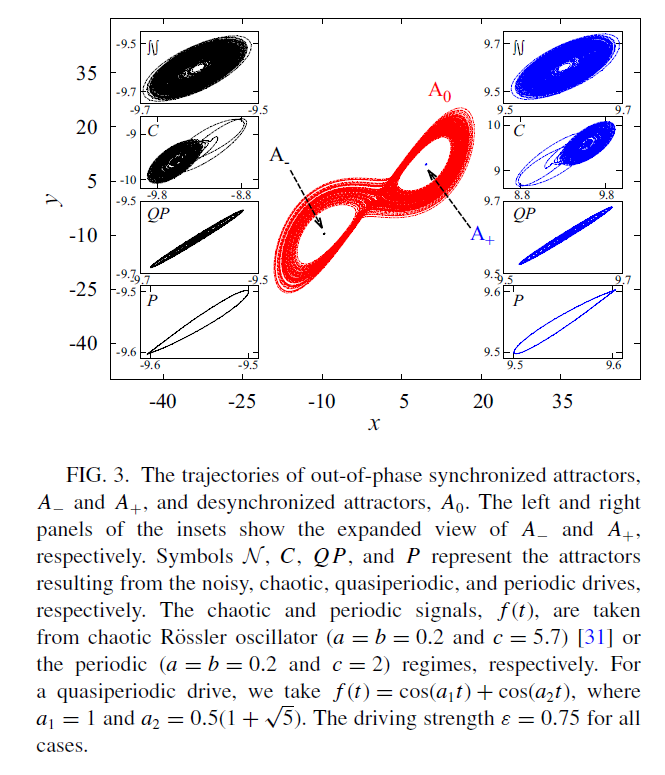
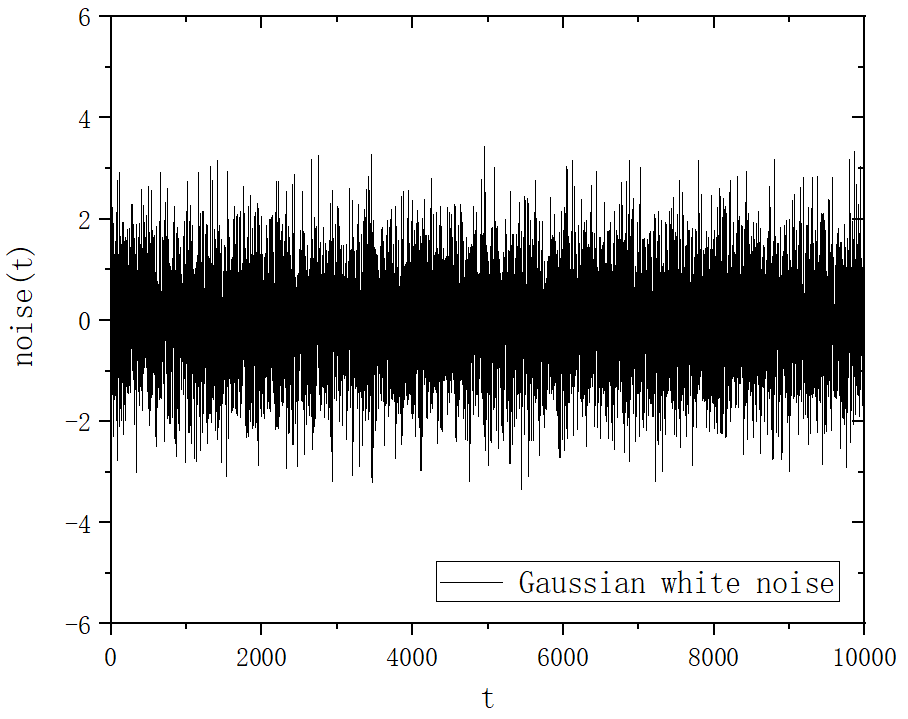
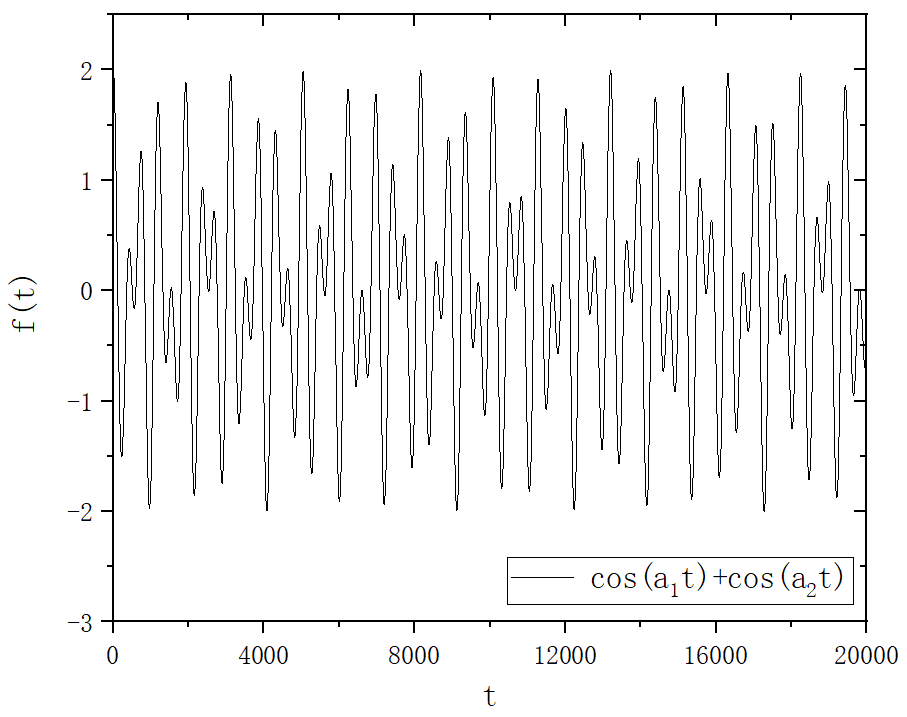
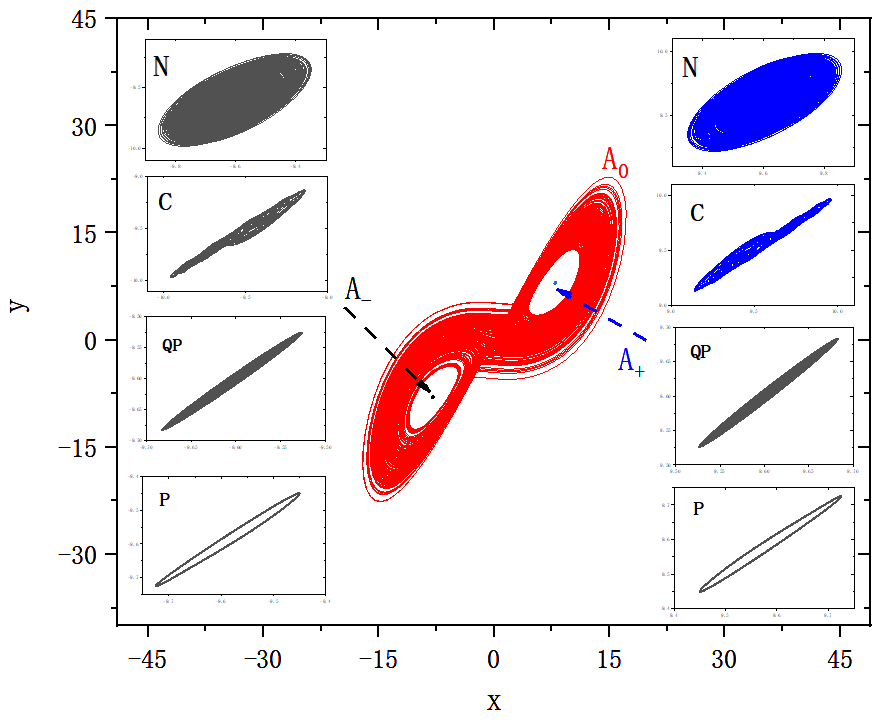
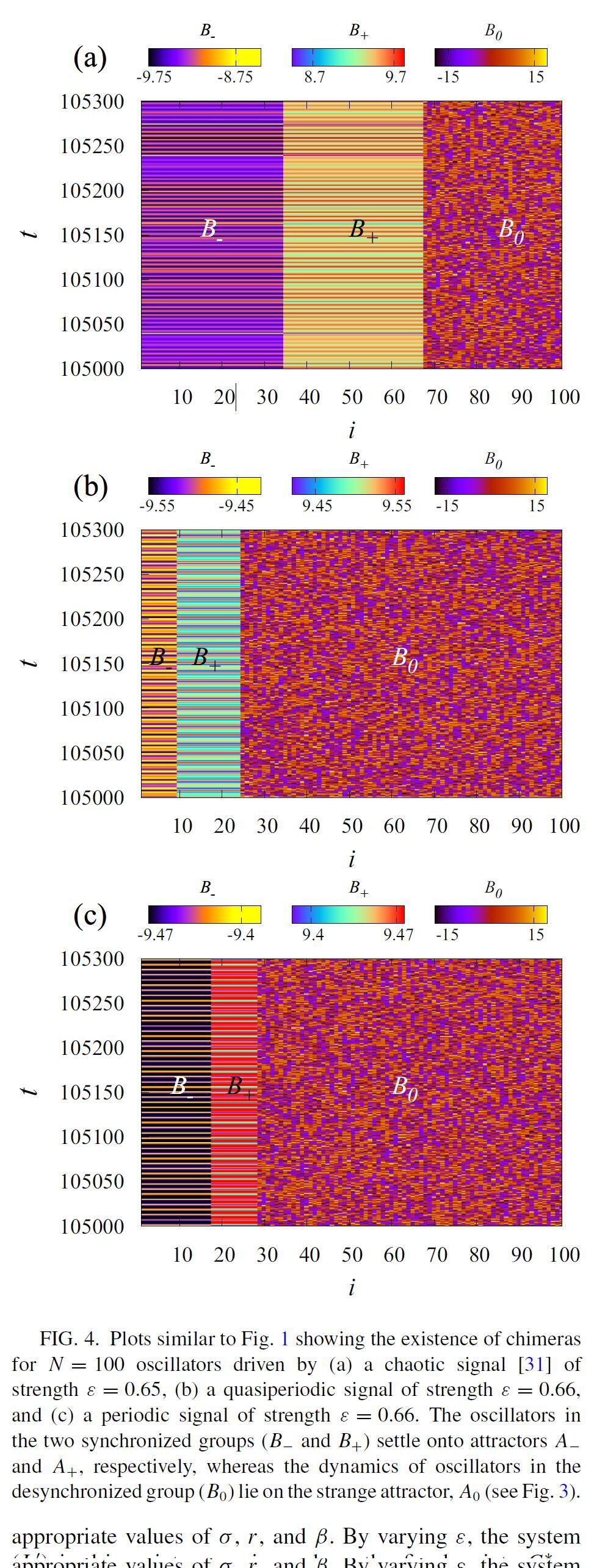
figure 4

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=10530000,T_trans=10500000,N=3,M=100
    real :: x(M,N),f(MaxT)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=x1*100.0-100.0
            x(i,2)=x2*100.0-100.0
            x(i,3)=x3*100.0-100.0
            write(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i,t)
        implicit none
        real :: xx(N),fx(N)
        integer :: t,i,j
        real :: a,b,c,K,epsilon
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=28.0 !r
        epsilon=0.65
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)+epsilon*(f(t)-xx(3))
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise

    !读取Rossler信号给f(t)
    subroutine Rossler_f()
        implicit none
        integer :: i
        real :: x1,x2,x3,x4
        open(12,file="Rossler_t_x_y_z.txt")
        do i=1,MaxT,1
            read(12,*) x1,x2,x3,x4
            f(i) = x2
        end do
        close(12)
        return
    end subroutine Rossler_f

    !cos(a1t)+cos(a2t)
    subroutine QP()
        implicit none
        real :: a1,a2
        integer :: i
        a1=1.0
        a2=0.5*(1.0+sqrt(5.0))
        do i=1,MaxT,1
            f(i)=cos(a1*i*h)+cos(a2*i*h)
        end do
        return
    end subroutine QP

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    call neighbour()
    call x0
    !call gaussNoise()
    call Rossler_f()
    !call QP()
    U_max=-1000.0
    U_min=1000.0
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call U_max_min(x(:,1),U_max,U_min)
            write(40,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(41,*) (t-T_trans)*h,x(4,1),x(4,2),x(4,3)
            write(42,*) (t-T_trans)*h,x(8,1),x(8,2),x(8,3)
            write(43,*) (t-T_trans)*h,x(17,1),x(17,2),x(17,3)
            write(44,*) (t-T_trans)*h,x(29,1),x(29,2),x(29,3)
            write(45,*) (t-T_trans)*h,x(20,1),x(20,2),x(20,3)
            write(46,*) (t-T_trans)*h,x(26,1),x(26,2),x(26,3)
            !将相同的动力学模式放在一起
            do i=1,M,1
                data(i,t-T_trans,1) = x(i,1)
                data(i,t-T_trans,2) = x(i,2)
                data(i,t-T_trans,3) = x(i,3)
            end do
        end if
    end do
    do i=1,M,1
        write(30,*) i,U_max(i),U_min(i)
        do t=1,MaxT-T_trans,1
            if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_max(i)<0) then
                !B-
                if(mod(t,100)==0) then
                    write(20,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_min(i)>0) then
                !B+
                if(mod(t,100)==0) then
                    write(21,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)-U_min(i)>5.0.and.U_min(i)<0.and.U_max(i)>0) then
                !B0
                if(mod(t,100)==0) then
                    write(22,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else
                write(60,*) "条件有误！"
            end if
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main

figure 4_A

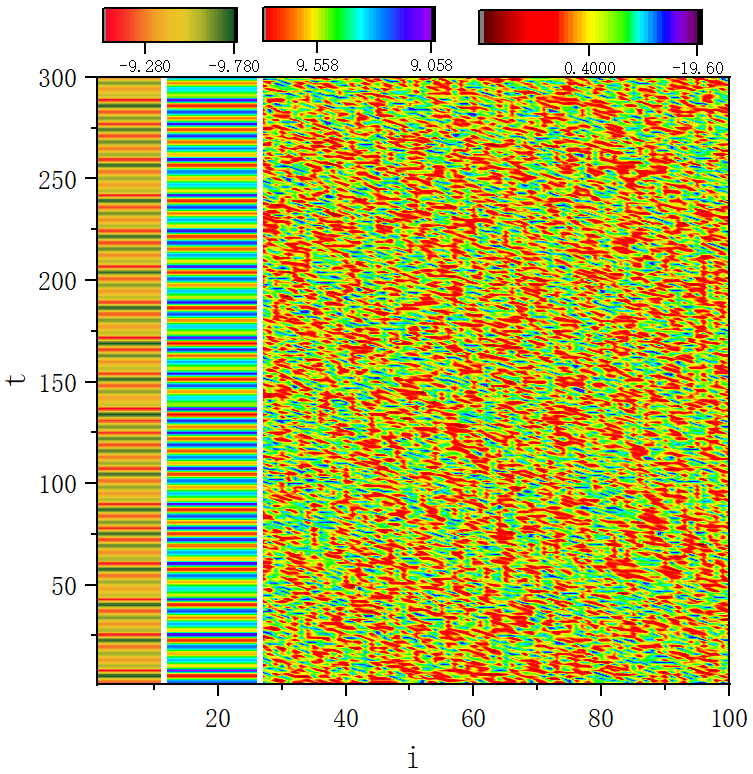
figure 4_B

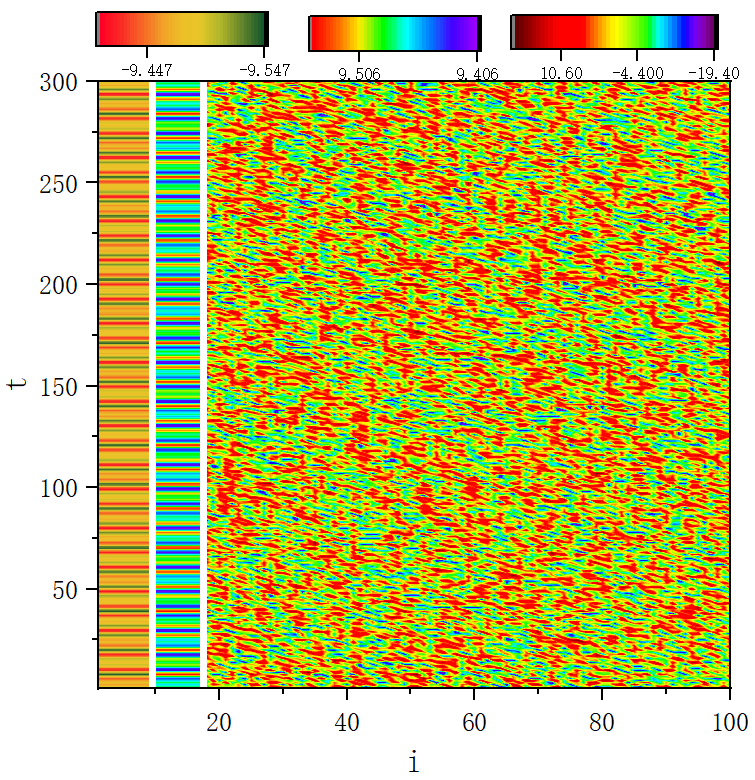
figure 4_C

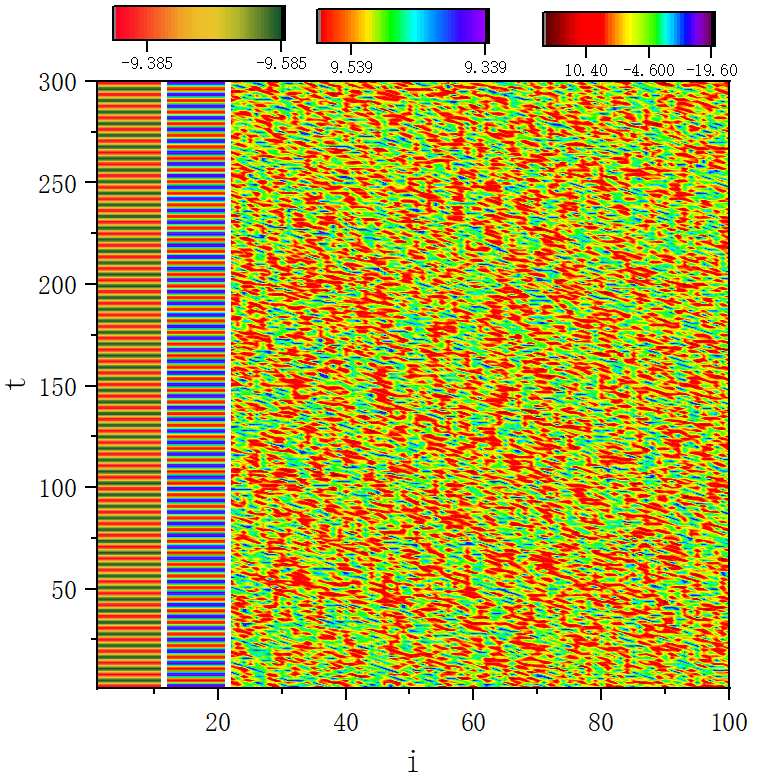
figure 5

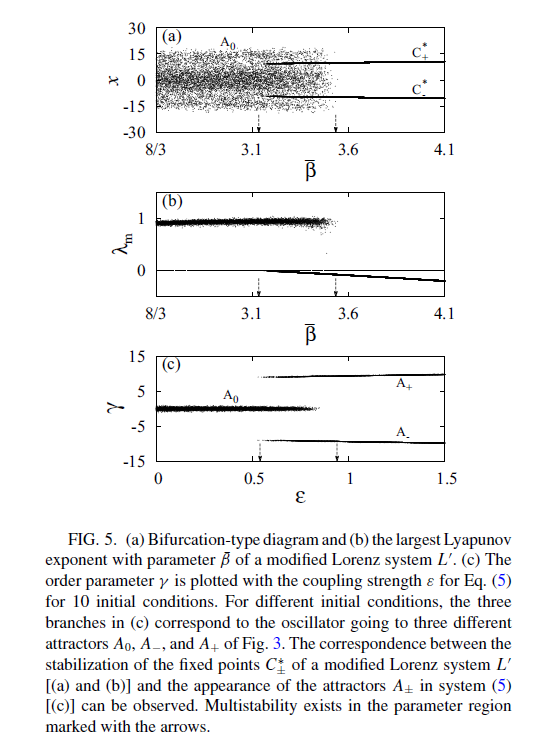
figure 5_A

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1060000,T_trans=1050000,N=3,M=10
    real :: x(M,N),f(MaxT),epsilon
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=x1*100.0-100.0
            x(i,2)=x2*100.0-100.0
            x(i,3)=x3*100.0-100.0
            write(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i,t)
        implicit none
        real :: xx(N),fx(N)
        integer :: t,i,j
        real :: a,b,c,beta_ave
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=28.0 !r
        beta_ave=(b+epsilon)
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-beta_ave*xx(3)+epsilon*f(t)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise

    !读取Rossler信号给f(t)
    subroutine Rossler_f()
        implicit none
        integer :: i
        real :: x1,x2,x3,x4
        open(12,file="Rossler_t_x_y_z.txt")
        do i=1,MaxT,1
            read(12,*) x1,x2,x3,x4
            f(i) = x2
        end do
        close(12)
        return
    end subroutine Rossler_f

    !cos(a1t)+cos(a2t)
    subroutine QP()
        implicit none
        real :: a1,a2
        integer :: i
        a1=1.0
        a2=0.5*(1.0+sqrt(5.0))
        do i=1,MaxT,1
            f(i)=cos(a1*i*h)+cos(a2*i*h)
            write(11,*) i,f(i)
        end do
        return
    end subroutine QP

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="beta_ave_x.txt")
    call neighbour()
!    call gaussNoise()
!    call Rossler_f()
    !call QP()
    do j=1,144,1
        call x0
        epsilon=j*0.01
        write(*,*) epsilon+8.0/3.0
        U_max=-1000.0
        U_min=1000.0
        f=0.0
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
                call U_max_min(x(:,1),U_max,U_min)
                if(mod(t,10000)==0) then
                    do i=1,M,1
                        write(60,*) epsilon+8.0/3.0,i,x(i,1)
                    end do    
                end if    
                !write(40,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
!                write(41,*) (t-T_trans)*h,x(4,1),x(4,2),x(4,3)
!                write(42,*) (t-T_trans)*h,x(8,1),x(8,2),x(8,3)
!                write(43,*) (t-T_trans)*h,x(17,1),x(17,2),x(17,3)
!                write(44,*) (t-T_trans)*h,x(29,1),x(29,2),x(29,3)
!                write(45,*) (t-T_trans)*h,x(20,1),x(20,2),x(20,3)
!                write(46,*) (t-T_trans)*h,x(26,1),x(26,2),x(26,3)
                !将相同的动力学模式放在一起
!                do i=1,M,1
!                    data(i,t-T_trans,1) = x(i,1)
!                    data(i,t-T_trans,2) = x(i,2)
!                    data(i,t-T_trans,3) = x(i,3)
!                end do
            end if
        end do
        do i=1,M,1
            write(30,*) epsilon+8.0/3.0,i,U_max(i),U_min(i)
!            do t=1,MaxT-T_trans,1
!                if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_max(i)<0) then
!                    !B-
!                    if(mod(t,100)==0) then
!                        write(20,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
!                    end if
!                else if(abs(U_max(i))-abs(U_min(i))<5.0.and.U_min(i)>0) then
!                    !B+
!                    if(mod(t,100)==0) then
!                        write(21,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
!                    end if
!                else if(U_max(i)-U_min(i)>5.0.and.U_min(i)<0.and.U_max(i)>0) then
!                    !B0
!                    if(mod(t,100)==0) then
!                        write(22,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
!                    end if
!                else
!                    write(60,*) "条件有误！"
!                end if
!            end do
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main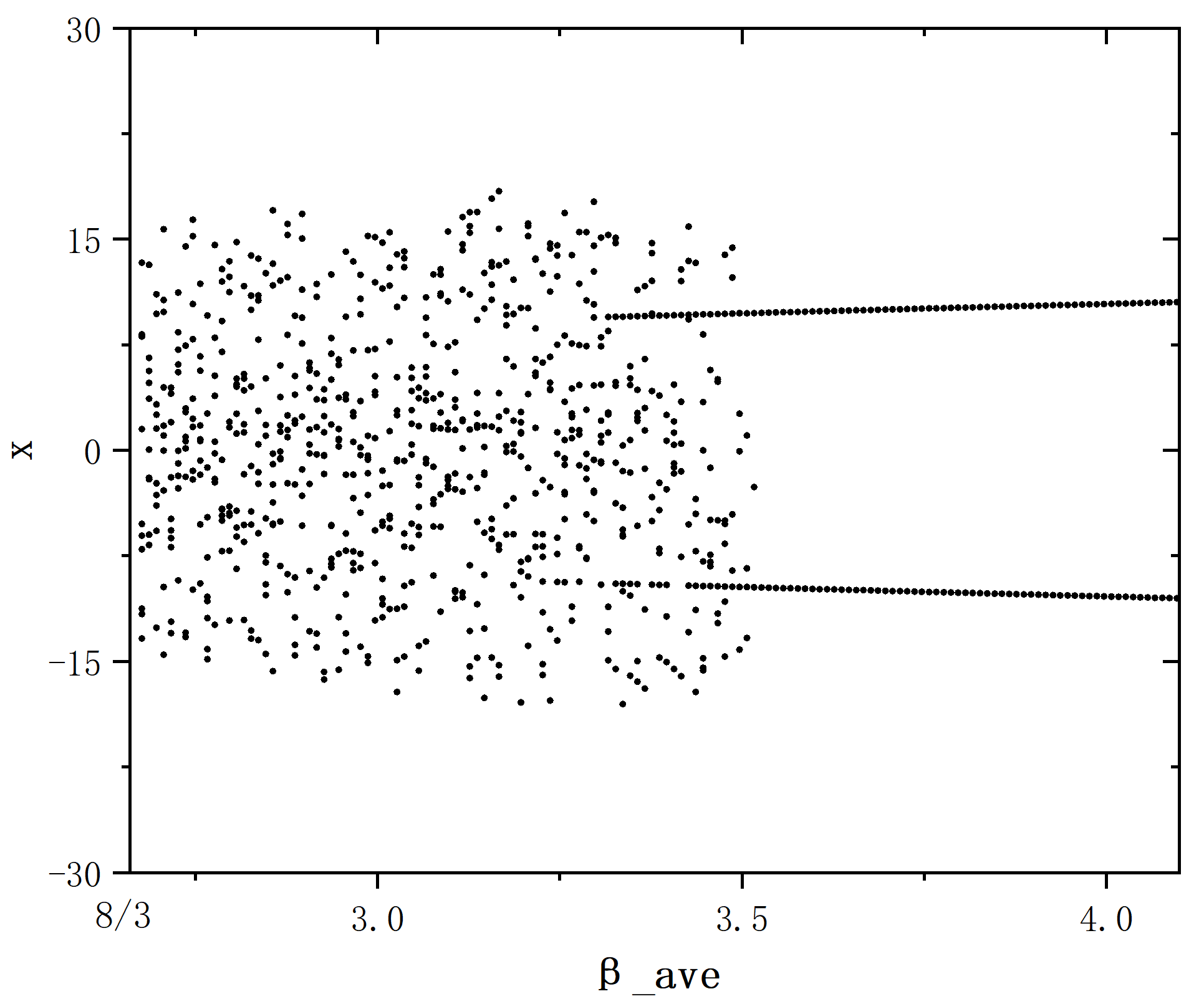

figure 5_B

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=250000,N=3,M=1,T_trans=200000
    real(kind=8) :: x1(M,N),x2(M,N),f(MaxT)
    real :: epsilon
contains

    subroutine x0()
        implicit none
        integer :: i
        real(kind=8) :: x11,x22,x33
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x11)
            call random_number(x22)
            call random_number(x33)
            x1(i,1)=x11*100.0-100.0
            x1(i,2)=x22*100.0-100.0
            x1(i,3)=x33*100.0-100.0
            write(5,*) x1(i,1),x1(i,2),x1(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,i,j
        real(kind=8) :: a,b,c,beta_ave
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=28.0 !r
        beta_ave=(b+epsilon)
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-beta_ave*xx(3)+epsilon*f(t)
        return
    end subroutine fnf


    subroutine rk4(x)
        implicit none
        integer :: i
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4


end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real(kind=8) :: d1=0.0,d0,lam,lamda
    open(10,file="beta_ave_lamda.txt")
    d0=1.0e-7
    !初值基准点
    do i=1,144,1
        do j=1,100,1
            lam=0.0
            lamda=0.0
            f=0.0
            epsilon=i*0.01
            call x0()
            x2=x1
            x2(1,3)=x1(1,3)+d0
            do t=1,MaxT,1
                call rk4(x1)
                call rk4(x2)
                d1=sqrt((x2(1,1)-x1(1,1))**2+(x2(1,2)-x1(1,2))**2+(x2(1,3)-x1(1,3))**2)
                !新的偏离点在上一次计算的两轨迹末端的连线上，且距离仍等于d0
                x2(1,1)=x1(1,1)+(d0/d1)*(x2(1,1)-x1(1,1))
                x2(1,2)=x1(1,2)+(d0/d1)*(x2(1,2)-x1(1,2))
                x2(1,3)=x1(1,3)+(d0/d1)*(x2(1,3)-x1(1,3))
                if(t>T_trans) then
                    lam=lam+log(d1/d0)
                end if
            end do
            lamda=lam/((MaxT-T_trans-1))/h
            write(10,*) j,epsilon+8.0/3.0,lamda
            write(*,*) j,epsilon+8.0/3.0,lamda
        end do
    end do
    close(10)
end program main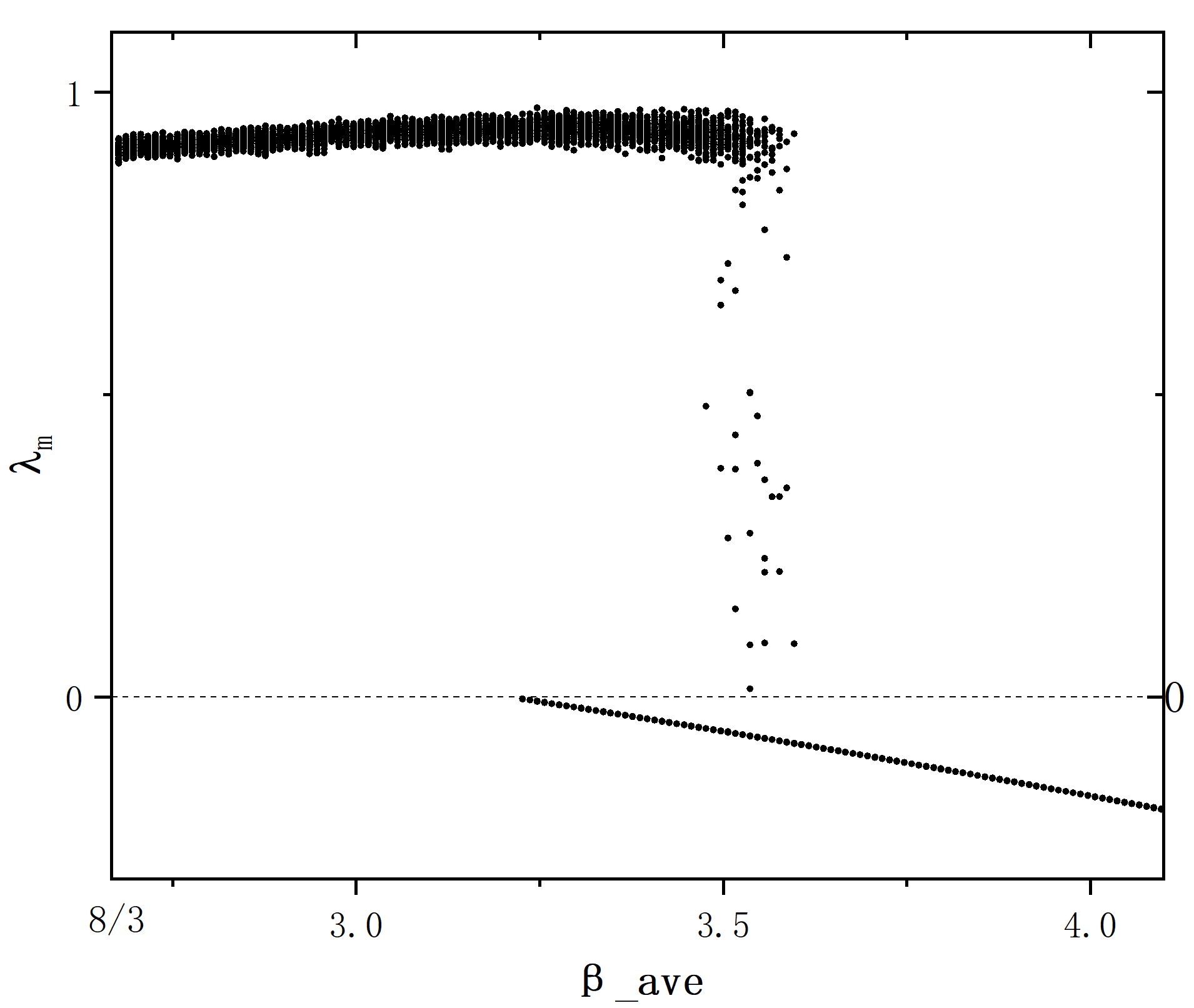

figure 5_C

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1060000,T_trans=1050000,N=3,M=100
    real :: x(M,N),f(MaxT),epsilon
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=x1*100.0-100.0
            x(i,2)=x2*100.0-100.0
            x(i,3)=x3*100.0-100.0
!            write(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i,t)
        implicit none
        real :: xx(N),fx(N)
        integer :: t,i,j
        real :: a,b,c
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=28.0 !r
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)+epsilon*(f(t)-xx(3))
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise

    !读取Rossler信号给f(t)
    subroutine Rossler_f()
        implicit none
        integer :: i
        real :: x1,x2,x3,x4
        open(12,file="Rossler_t_x_y_z.txt")
        do i=1,MaxT,1
            read(12,*) x1,x2,x3,x4
            f(i) = x2
        end do
        close(12)
        return
    end subroutine Rossler_f

    !cos(a1t)+cos(a2t)
    subroutine QP()
        implicit none
        real :: a1,a2
        integer :: i
        a1=1.0
        a2=0.5*(1.0+sqrt(5.0))
        do i=1,MaxT,1
            f(i)=cos(a1*i*h)+cos(a2*i*h)
            write(11,*) i,f(i)
        end do
        return
    end subroutine QP

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="beta_ave_x.txt")
    call neighbour()
    !    call Rossler_f()
    !call QP()
    do j=1,151,1
        call x0
        epsilon=j*0.01-0.01
        write(*,*) epsilon
        U_max=-1000.0
        U_min=1000.0
        call gaussNoise()
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
                call U_max_min(x(:,1),U_max,U_min)
            end if
        end do
        do i=1,M,1
            write(30,*) epsilon,i,(U_max(i)+U_min(i))/2.0
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main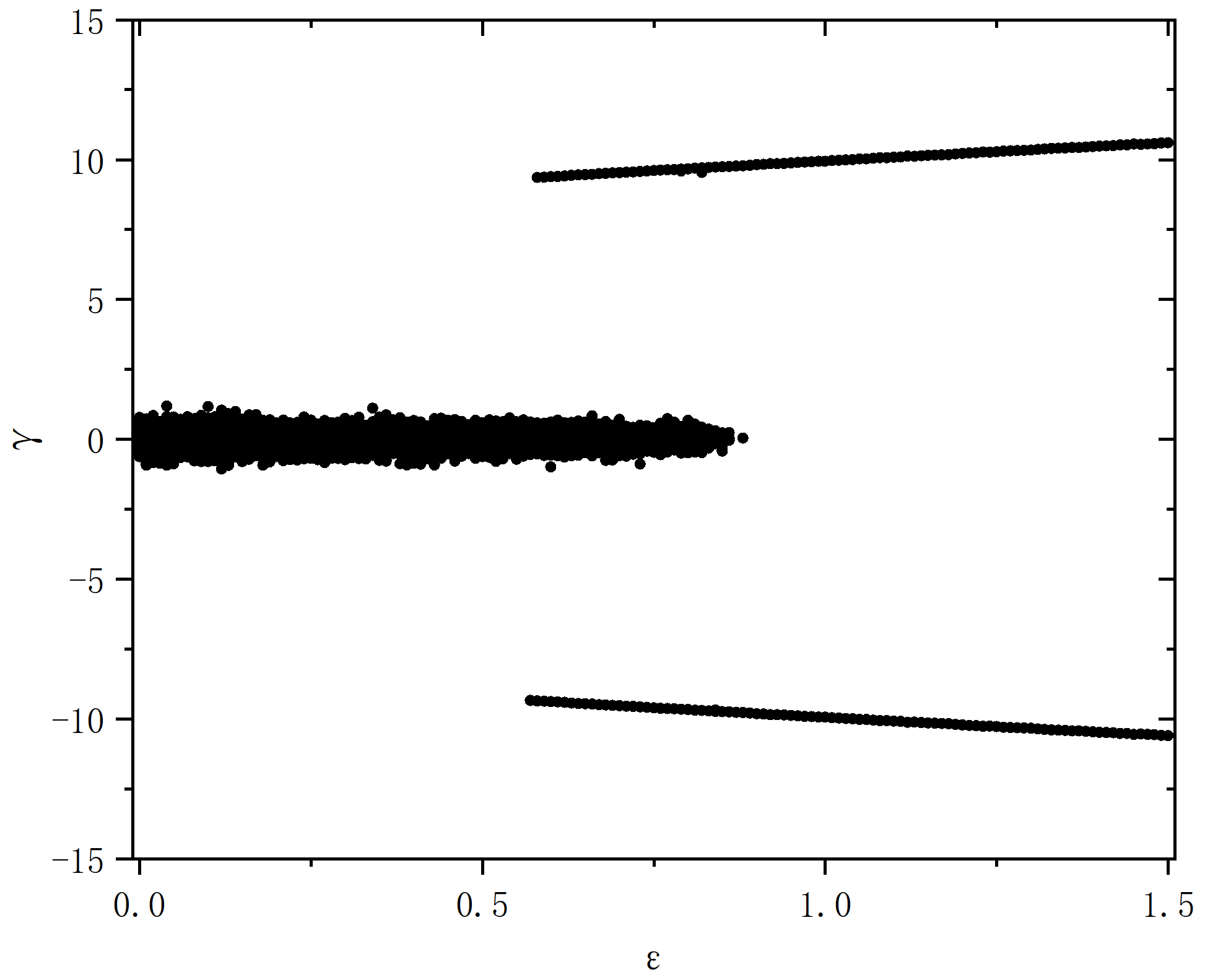

figure 6

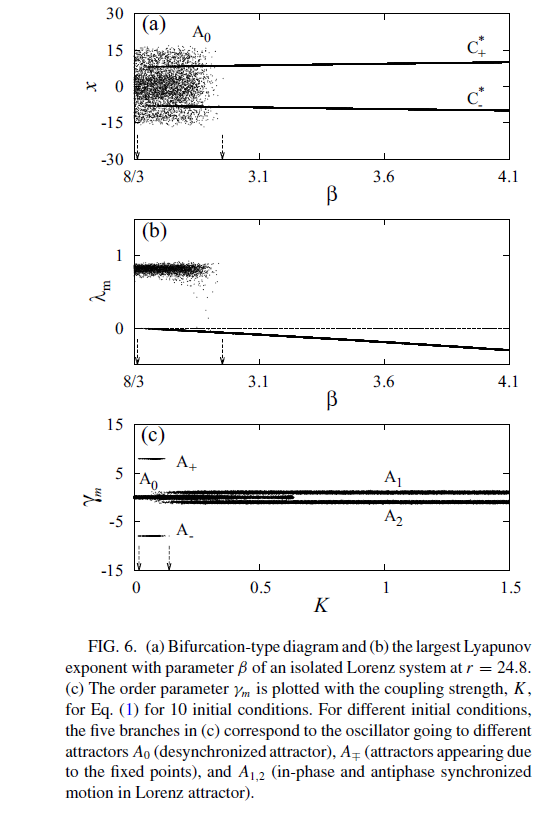
figure 6_A

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1060000,T_trans=1050000,N=3,M=50
    real :: x(M,N),f(MaxT),beta
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=x1*100.0-100.0
            x(i,2)=x2*100.0-100.0
            x(i,3)=x3*100.0-100.0
            write(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i,t)
        implicit none
        real :: xx(N),fx(N)
        integer :: t,i,j
        real :: a,b,c
        a=10.0 !sigma
        b=beta !beta
        c=24.8 !r
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise

    !读取Rossler信号给f(t)
    subroutine Rossler_f()
        implicit none
        integer :: i
        real :: x1,x2,x3,x4
        open(12,file="Rossler_t_x_y_z.txt")
        do i=1,MaxT,1
            read(12,*) x1,x2,x3,x4
            f(i) = x2
        end do
        close(12)
        return
    end subroutine Rossler_f

    !cos(a1t)+cos(a2t)
    subroutine QP()
        implicit none
        real :: a1,a2
        integer :: i
        a1=1.0
        a2=0.5*(1.0+sqrt(5.0))
        do i=1,MaxT,1
            f(i)=cos(a1*i*h)+cos(a2*i*h)
            write(11,*) i,f(i)
        end do
        return
    end subroutine QP

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="beta_ave_x.txt")
    call neighbour()
!    call gaussNoise()
!    call Rossler_f()
    !call QP()
    do j=1,145,1
        call x0
        beta=8.0/3.0+j*0.01-0.01
        write(*,*) beta
        U_max=-1000.0
        U_min=1000.0
        f=0.0
        do t=1,MaxT,1
            call rk4(x,t)
            if(t>T_trans) then
                call U_max_min(x(:,1),U_max,U_min)
                if(mod(t,10000)==0) then
                    do i=1,M,1
                        write(60,*) beta,i,x(i,1)
                    end do    
                end if    
            end if
        end do
        do i=1,M,1
            write(30,*) beta,i,U_max(i),U_min(i)
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main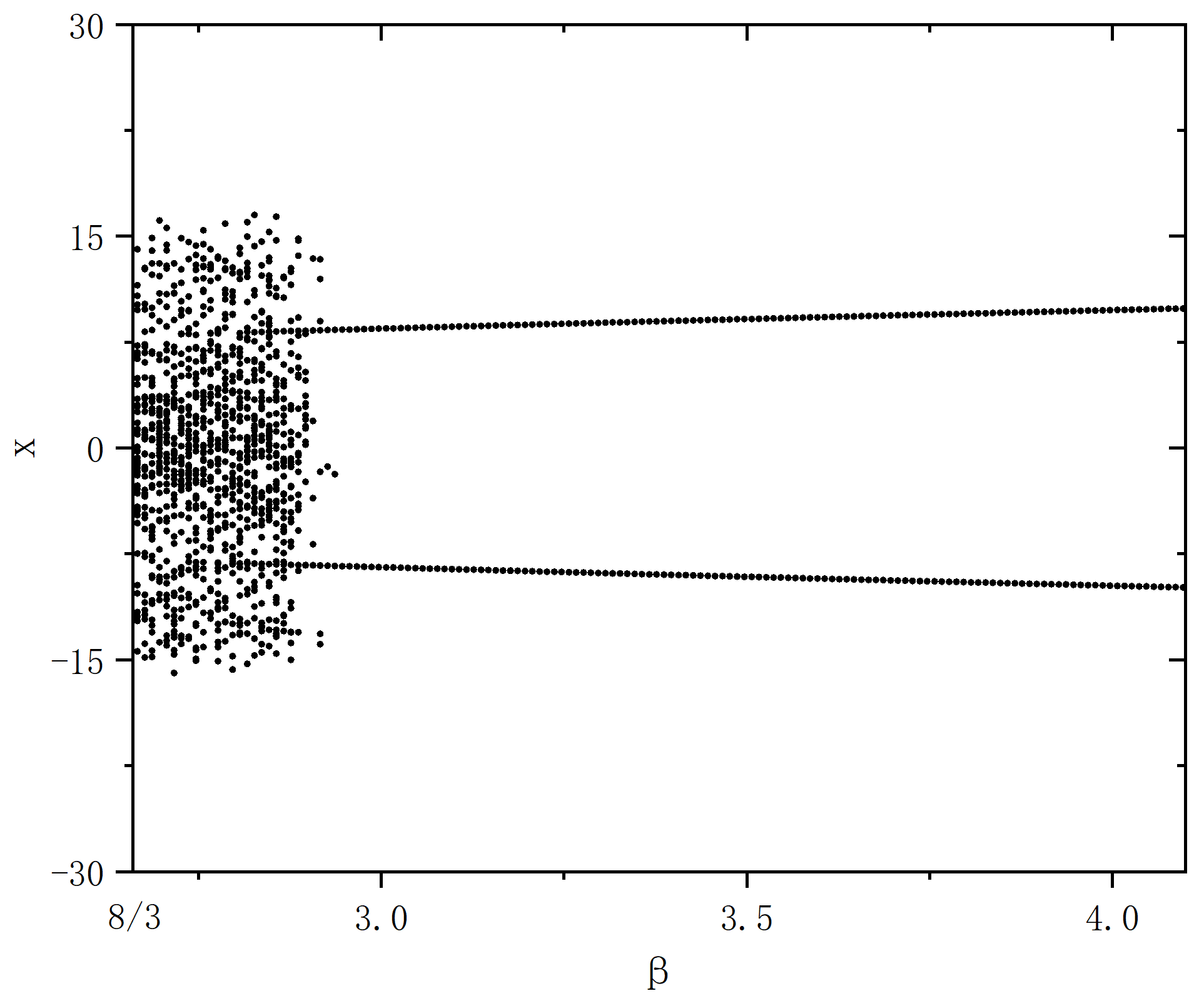

figure 6_B

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=250000,N=3,M=1,T_trans=200000
    real(kind=8) :: x1(M,N),x2(M,N),f(MaxT)
    real :: beta
contains

    subroutine x0()
        implicit none
        integer :: i
        real(kind=8) :: x11,x22,x33
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x11)
            call random_number(x22)
            call random_number(x33)
            x1(i,1)=x11*100.0-100.0
            x1(i,2)=x22*100.0-100.0
            x1(i,3)=x33*100.0-100.0
            write(5,*) x1(i,1),x1(i,2),x1(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real(kind=8) :: xx(N),fx(N)
        integer :: t,i,j
        real(kind=8) :: a,b,c
        a=10.0 !sigma
        b=beta !beta
        c=24.8 !r
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)
        return
    end subroutine fnf


    subroutine rk4(x)
        implicit none
        integer :: i
        real(kind=8) :: x(M,N),xx(N),fx(N)
        real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4


end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j
    real(kind=8) :: d1=0.0,d0,lam,lamda
    open(10,file="beta_ave_lamda.txt")
    d0=1.0e-7
    !初值基准点
    do i=1,144,1
        do j=1,100,1
            lam=0.0
            lamda=0.0
            f=0.0
            beta=i*0.01+8.0/3.0
            call x0()
            x2=x1
            x2(1,3)=x1(1,3)+d0
            do t=1,MaxT,1
                call rk4(x1)
                call rk4(x2)
                d1=sqrt((x2(1,1)-x1(1,1))**2+(x2(1,2)-x1(1,2))**2+(x2(1,3)-x1(1,3))**2)
                !新的偏离点在上一次计算的两轨迹末端的连线上，且距离仍等于d0
                x2(1,1)=x1(1,1)+(d0/d1)*(x2(1,1)-x1(1,1))
                x2(1,2)=x1(1,2)+(d0/d1)*(x2(1,2)-x1(1,2))
                x2(1,3)=x1(1,3)+(d0/d1)*(x2(1,3)-x1(1,3))
                if(t>T_trans) then
                    lam=lam+log(d1/d0)
                end if
            end do
            lamda=lam/((MaxT-T_trans-1))/h
            write(10,*) j,beta,lamda
            write(*,*) j,beta,lamda
        end do
    end do
    close(10)
end program main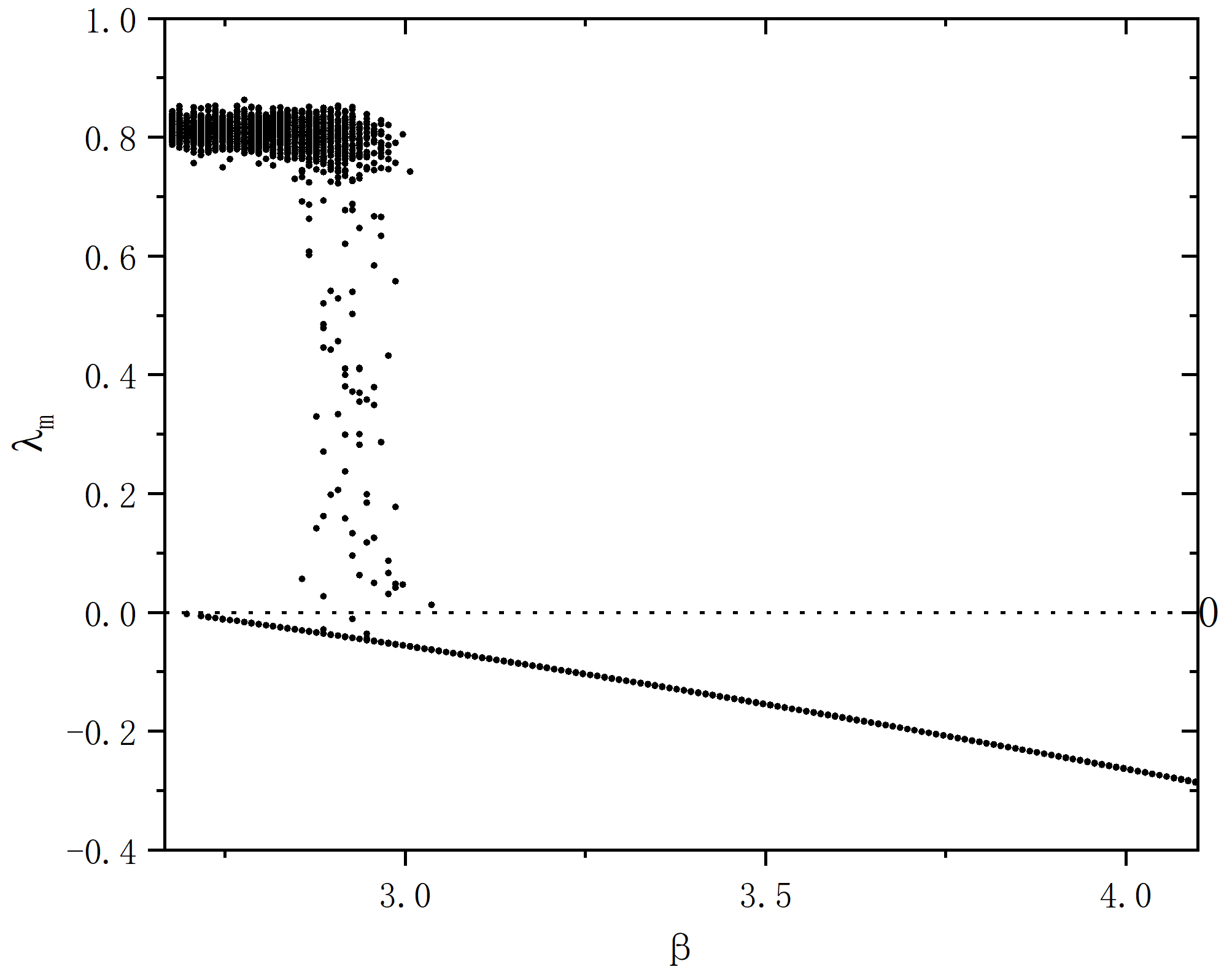

figure 6_C

 module Lorenz
     implicit none
     real,parameter :: h=0.01
     integer,parameter :: MaxT=1060000,T_trans=1050000,N=3,M=10
     real :: x(M,N),f(MaxT),K
     integer,allocatable :: neighbour_matrix(:,:)
 contains

     subroutine x0()
         implicit none
         integer :: i
         real :: x1,x2,x3
         call random_seed()
         open(5,file="x0_y0_z0.txt")
         do i=1,M,1
             call random_number(x1)
             call random_number(x2)
             call random_number(x3)
             x(i,1)=x1*100.0-100.0
             x(i,2)=x2*100.0-100.0
             x(i,3)=x3*100.0-100.0
             !            write(5,*) x(i,1),x(i,2),x(i,3)
         end do
         close(5)
     end subroutine x0

     subroutine fnf(xx,fx,i,t)
         implicit none
         real :: xx(N),fx(N),coupling
         integer :: t,i,j
         real :: a,b,c
         a=10.0 !sigma
         b=8.0/3.0 !beta
         c=24.74 !r
         coupling=0.0
         do j=1,M,1
             coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
         end do
         fx(1)=a*(xx(2)-xx(1))
         fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
         fx(3)=xx(1)*xx(2)-b*xx(3)+(K/real(M-1))*coupling
         return
     end subroutine fnf


     subroutine rk4(x,t)
         implicit none
         integer :: i,t
         real :: x(M,N),xx(N),fx(N)
         real :: kx1(N),kx2(N),kx3(N),kx4(N)
         do i=1,M,1
             xx=x(i,:)
             call fnf(xx,fx,i,t)
             kx1=h*fx
             xx=x(i,:)+0.5*kx1
             call fnf(xx,fx,i,t)
             kx2=h*fx
             xx=x(i,:)+0.5*kx2
             call fnf(xx,fx,i,t)
             kx3=h*fx
             xx=x(i,:)+kx3
             call fnf(xx,fx,i,t)
             kx4=h*fx
             x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
         end do
         return
     end subroutine rk4

     !Umax与Umin
     subroutine U_max_min(xxx,U_max,U_min)
         implicit none
         real :: U_max(M),U_min(M),xxx(M)
         integer :: i
         do i=1,M,1
             if(U_max(i)<xxx(i)) then
                 U_max(i)=xxx(i)
             end if
             if(U_min(i)>xxx(i)) then
                 U_min(i)=xxx(i)
             end if
         end do
         return
     end subroutine U_max_min

     !建立网络结构
     subroutine neighbour()
         implicit none
         integer :: K !单节点K个邻居
         integer :: i,j,number
         allocate(neighbour_matrix(M,M))
         !初始化网络矩阵
         neighbour_matrix=0
         do i=1,M-1,1
             do j=i+1,M,1
                 neighbour_matrix(i,j)=1
                 neighbour_matrix(j,i)=1
             end do
         end do
         !输出矩阵
         do i=1,M,1
             do j=1,M,1
                 write(10,"(I2)",advance='no') neighbour_matrix(i,j)
             end do
             write(10,*)
         end do
         return
     end subroutine neighbour

     !普通高斯白噪声
     subroutine gaussNoise()
         implicit none
         integer, parameter :: L = MaxT ! 生成噪声的长度
         real,parameter :: pi=3.1415926
         real :: noise(L)            ! 储存噪声的数组
         real :: mean = 0.0         ! 均值
         real :: std_dev = 1.0       ! 标准差
         integer :: seed = 1         ! 随机数种子
         integer :: i
         open(11,file="noise.txt")
         ! 生成噪声
         call random_seed()
         do i = 1, L
             call random_number(noise(i))
         end do
         do i=1,L-1
             noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
         end do
         noise(L)=0.0
         ! 输出噪声
         do i = 1, L
             f(i)=noise(i)
             write(11,*) i,noise(i)
         end do
         return
     end subroutine gaussNoise

     !读取Rossler信号给f(t)
     subroutine Rossler_f()
         implicit none
         integer :: i
         real :: x1,x2,x3,x4
         open(12,file="Rossler_t_x_y_z.txt")
         do i=1,MaxT,1
             read(12,*) x1,x2,x3,x4
             f(i) = x2
         end do
         close(12)
         return
     end subroutine Rossler_f

     !cos(a1t)+cos(a2t)
     subroutine QP()
         implicit none
         real :: a1,a2
         integer :: i
         a1=1.0
         a2=0.5*(1.0+sqrt(5.0))
         do i=1,MaxT,1
             f(i)=cos(a1*i*h)+cos(a2*i*h)
             write(11,*) i,f(i)
         end do
         return
     end subroutine QP

 end module Lorenz



 program main
     use Lorenz
     implicit none
     integer :: t,i,j
     real :: U_max(M),U_min(M),gamma_m,gamma,gamma_state,x_direction(M,2),y_direction(M,2)
     open(10,file="neighbour_matrix.txt")
     open(20,file="i_t_x_B-.txt")
     open(21,file="i_t_x_B+.txt")
     open(22,file="i_t_x_B0.txt")
     open(30,file="xmax_xmin.txt")
     open(40,file="t_x_1.txt")
     open(41,file="t_x_4.txt")
     open(42,file="t_x_8.txt")
     open(43,file="t_x_17.txt")
     open(44,file="t_x_29.txt")
     open(45,file="t_x_20.txt")
     open(46,file="t_x_26.txt")
     open(50,file="t_x_1_data.txt")
     open(60,file="beta_ave_x.txt")
     open(70,file="i_K_gamma_m.txt")
     call neighbour()
     !call Rossler_f()
     !call QP()
     !call gaussNoise()
     do j=1,151,1
         call x0
         K=j*0.01-0.01
 !        write(*,*) K
         U_max=-1000.0
         U_min=1000.0
         x_direction=0.0
         y_direction=0.0
         gamma_state=0.0
         do t=1,MaxT,1
             call rk4(x,t)
             if(t>T_trans) then
                 call U_max_min(x(:,1),U_max,U_min)
                 if(t==T_trans+10) then
                     x_direction(:,1)=x(:,1)
                     y_direction(:,1)=x(:,2)
                 end if
                 if(t==T_trans+5) then
                     x_direction(:,2)=x(:,1)
                     y_direction(:,2)=x(:,2)
                 end if
             end if
         end do
         do i=1,M,1
             gamma=(U_max(i)+U_min(i))/2.0
             !判断：同相运动gamma_state=1，反向运动gamma_state=-1，去同步gamma_state=0
 !            if((U_max(i)>0.0.and.U_max(i)>0.0).or.(U_max(i)<0.0.and.U_max(i)<0.0).and.abs(U_max(i))-abs(U_min(i))<1.0) then
 !                gamma_state=0.0
 !            else if(U_max(i)>0.0.and.U_min(i)<0.0) then
 !                if(x_direction(i,1)>0.0.and.y_direction(i,1)>0.0) then
 !                    !第一象限
 !                    if(x_direction(i,1)<x_direction(i,2)) then
 !                        gamma_state=1.0
 !                    else
 !                        gamma_state=-1.0
 !                    end if
 !                else if(x_direction(i,1)<0.0.and.y_direction(i,1)>0.0) then
 !                    !第二象限
 !                    if(x_direction(i,1)<x_direction(i,2)) then
 !                        gamma_state=1.0
 !                    else
 !                        gamma_state=-1.0
 !                    end if
 !                else if(x_direction(i,1)<0.0.and.y_direction(i,1)<0.0)  then
 !                    !第三象限
 !                    if(x_direction(i,1)>x_direction(i,2)) then
 !                        gamma_state=1.0
 !                    else
 !                        gamma_state=-1.0
 !                    end if
 !                else if(x_direction(i,1)>0.0.and.y_direction(i,1)<0.0) then
 !                    !第四象限
 !                    if(x_direction(i,1)>x_direction(i,2)) then
 !                        gamma_state=1.0
 !                    else
 !                        gamma_state=-1.0
 !                    end if
 !                end if
 !            end if
 !            gamma_m=gamma+gamma_state
             write(70,*) i,K,gamma
             write(*,*) i,K,gamma
         end do
     end do
     close(10)
     close(20)
     close(30)
     close(40)
     deallocate(neighbour_matrix)
 end program main

figure 7

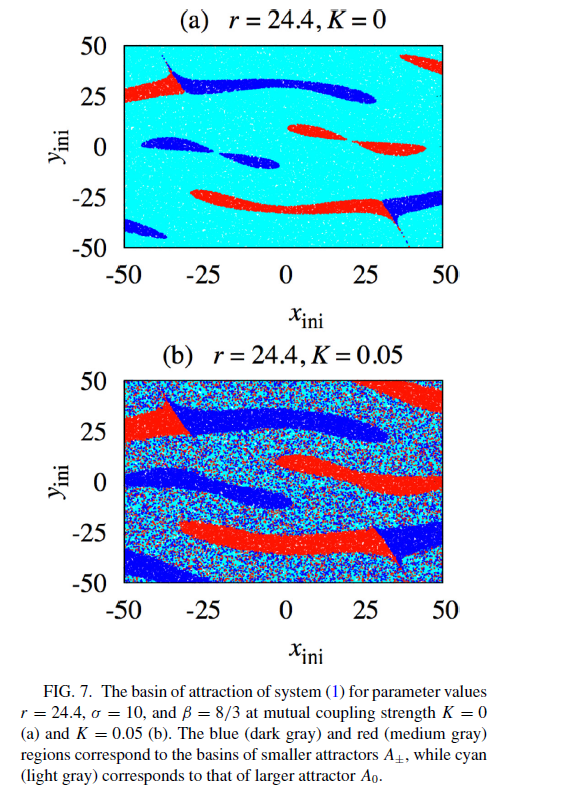
figure 7_A

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1060000,T_trans=1050000,N=3,M=10
    real :: x(M,N),f(MaxT)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0(xini,yini)
        implicit none
        integer :: i
        do i=1,M,1
            x(i,1)=xini
            x(i,2)=yini
            x(i,3)=0.0
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real :: xx(N),fx(N),coupling
        integer :: t,i,j
        real :: a,b,c,K
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=24.4 !r
        coupling=0.0
        K=0.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
        end do
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)+(K/real(M-1))*coupling
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise

    !读取Rossler信号给f(t)
    subroutine Rossler_f()
        implicit none
        integer :: i
        real :: x1,x2,x3,x4
        open(12,file="Rossler_t_x_y_z.txt")
        do i=1,MaxT,1
            read(12,*) x1,x2,x3,x4
            f(i) = x2
        end do
        close(12)
        return
    end subroutine Rossler_f

    !cos(a1t)+cos(a2t)
    subroutine QP()
        implicit none
        real :: a1,a2
        integer :: i
        a1=1.0
        a2=0.5*(1.0+sqrt(5.0))
        do i=1,MaxT,1
            f(i)=cos(a1*i*h)+cos(a2*i*h)
            write(11,*) i,f(i)
        end do
        return
    end subroutine QP

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j,jj,state
    real :: U_max(M),U_min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="beta_ave_x.txt")
    open(70,file="i_K_gamma_m.txt")
    open(80,file="xini_yini_state.txt")
    call neighbour()
    !call Rossler_f()
    !call QP()
    !call gaussNoise()
    do j=-50,50,1
        do jj=-50,50,1
            call x0(j,jj)
            write(*,*) j,jj
            U_max=-1000.0
            U_min=1000.0
            do t=1,MaxT,1
                call rk4(x,t)
                if(t>T_trans) then
                    call U_max_min(x(:,1),U_max,U_min)
                end if
            end do
            do i=1,M,1
                state=0
                if(U_max(i)>0.0.and.U_min(i)>0.0.and.(U_max(i)-U_min(i)<2.0)) then
                    !正稳定点
                    state=1
                else if(U_max(i)<0.0.and.U_min(i)<0.0.and.(U_max(i)-U_min(i)<2.0)) then
                    !负稳定点
                    state=2
                else if(U_max(i)>0.0.and.U_min(i)<0.0.and.(U_max(i)-U_min(i)>10.0)) then
                    !奇异吸引子
                    state=3
                end if
                write(80,*) j,jj,state
            end do
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main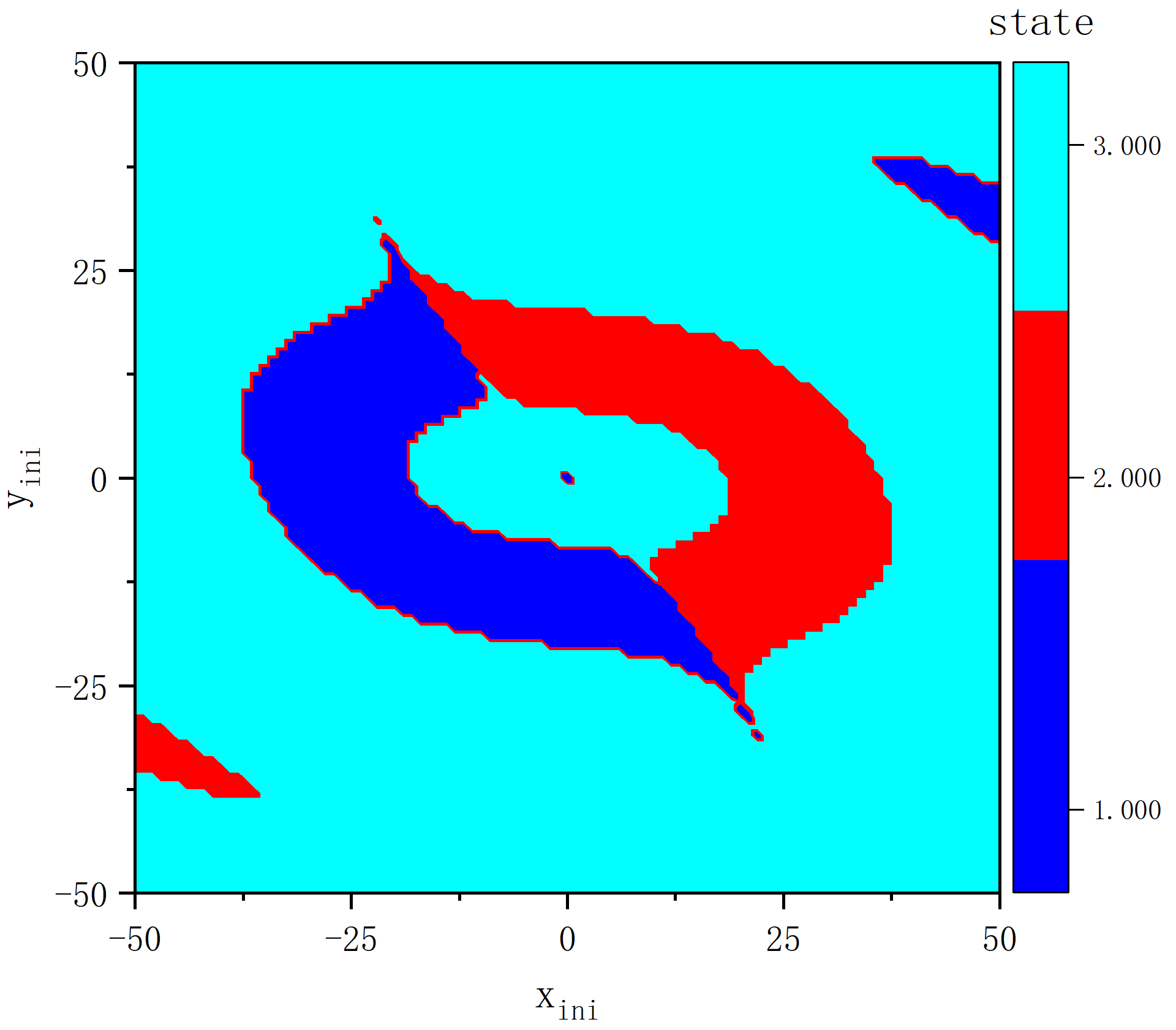

figure 7_B

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1060000,T_trans=1050000,N=3,M=10
    real :: x(M,N),f(MaxT)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0(xini,yini)
        implicit none
        integer :: i
        do i=1,M,1
            x(i,1)=xini
            x(i,2)=yini
            x(i,3)=0.0
        end do
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real :: xx(N),fx(N),coupling
        integer :: t,i,j
        real :: a,b,c,K
        a=10.0 !sigma
        b=8.0/3.0 !beta
        c=24.4 !r
        coupling=0.0
        K=0.05
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
        end do
        fx(1)=a*(xx(2)-xx(1))
        fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
        fx(3)=xx(1)*xx(2)-b*xx(3)+(K/real(M-1))*coupling
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: K !单节点K个邻居
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 1.0       ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise

    !读取Rossler信号给f(t)
    subroutine Rossler_f()
        implicit none
        integer :: i
        real :: x1,x2,x3,x4
        open(12,file="Rossler_t_x_y_z.txt")
        do i=1,MaxT,1
            read(12,*) x1,x2,x3,x4
            f(i) = x2
        end do
        close(12)
        return
    end subroutine Rossler_f

    !cos(a1t)+cos(a2t)
    subroutine QP()
        implicit none
        real :: a1,a2
        integer :: i
        a1=1.0
        a2=0.5*(1.0+sqrt(5.0))
        do i=1,MaxT,1
            f(i)=cos(a1*i*h)+cos(a2*i*h)
            write(11,*) i,f(i)
        end do
        return
    end subroutine QP

end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j,jj,state
    real :: U_max(M),U_min(M)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_4.txt")
    open(42,file="t_x_8.txt")
    open(43,file="t_x_17.txt")
    open(44,file="t_x_29.txt")
    open(45,file="t_x_20.txt")
    open(46,file="t_x_26.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="beta_ave_x.txt")
    open(70,file="i_K_gamma_m.txt")
    open(80,file="xini_yini_state.txt")
    call neighbour()
    !call Rossler_f()
    !call QP()
    !call gaussNoise()
    do j=-50,50,1
        do jj=-50,50,1
            call x0(j,jj)
            write(*,*) j,jj
            U_max=-1000.0
            U_min=1000.0
            do t=1,MaxT,1
                call rk4(x,t)
                if(t>T_trans) then
                    call U_max_min(x(:,1),U_max,U_min)
                end if
            end do
            do i=1,M,1
                state=0
                if(U_max(i)>0.0.and.U_min(i)>0.0.and.(U_max(i)-U_min(i)<2.0)) then
                    !正稳定点
                    state=1
                else if(U_max(i)<0.0.and.U_min(i)<0.0.and.(U_max(i)-U_min(i)<2.0)) then
                    !负稳定点
                    state=2
                else if(U_max(i)>0.0.and.U_min(i)<0.0.and.(U_max(i)-U_min(i)>10.0)) then
                    !奇异吸引子
                    state=3
                end if
                write(80,*) j,jj,state
            end do
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main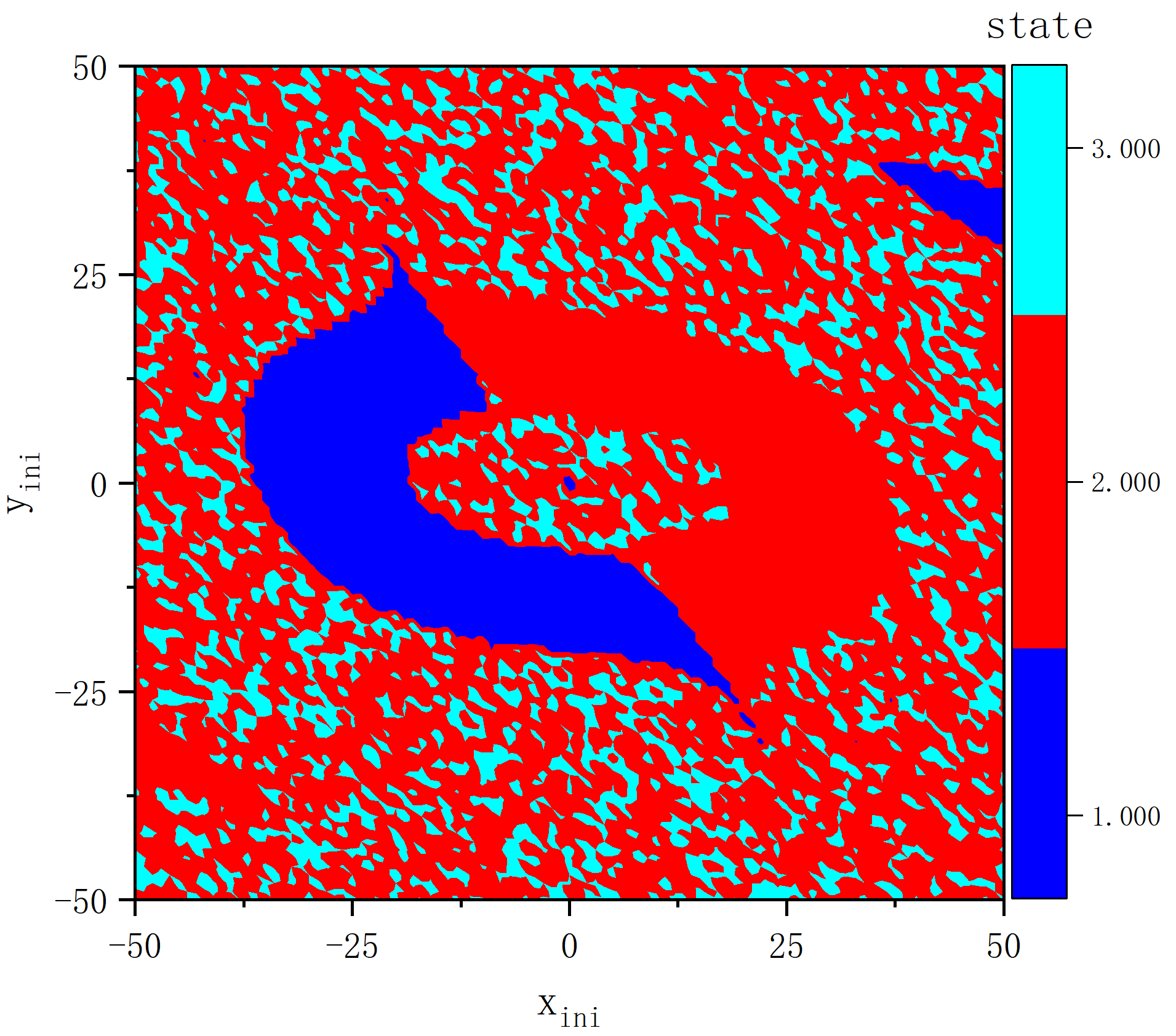

figure 8

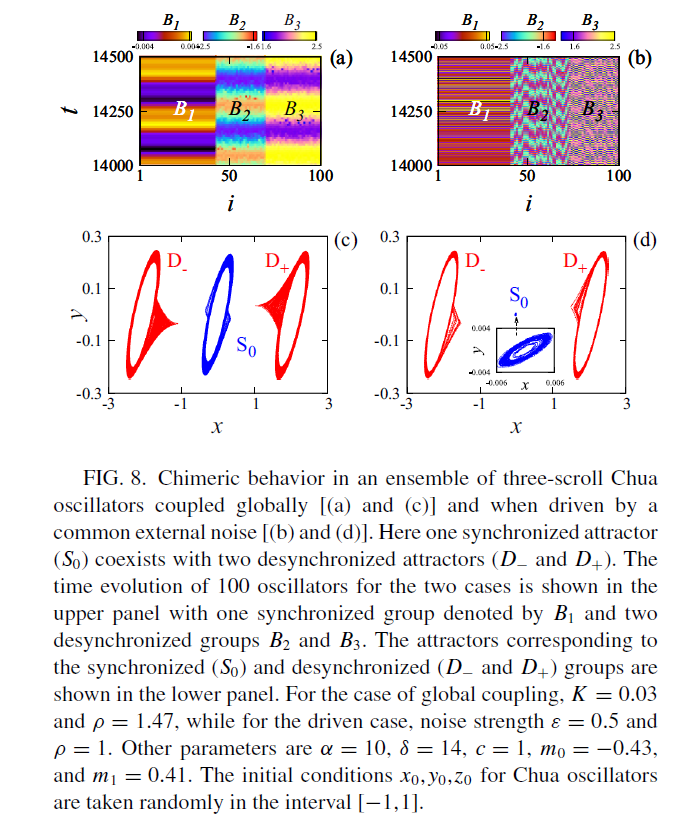
无耦合无外部调制作用(单节点)

• ρ=1.47

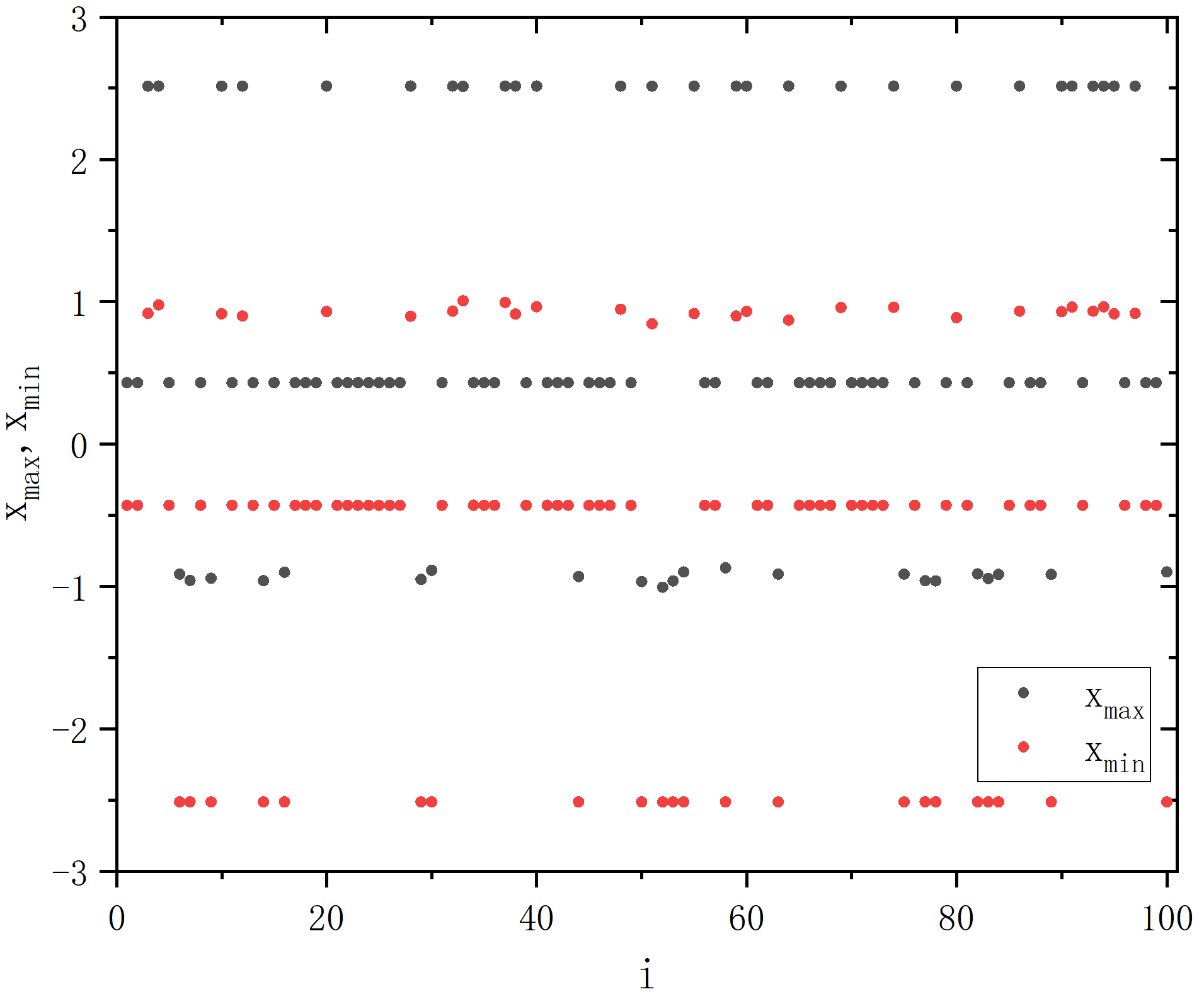
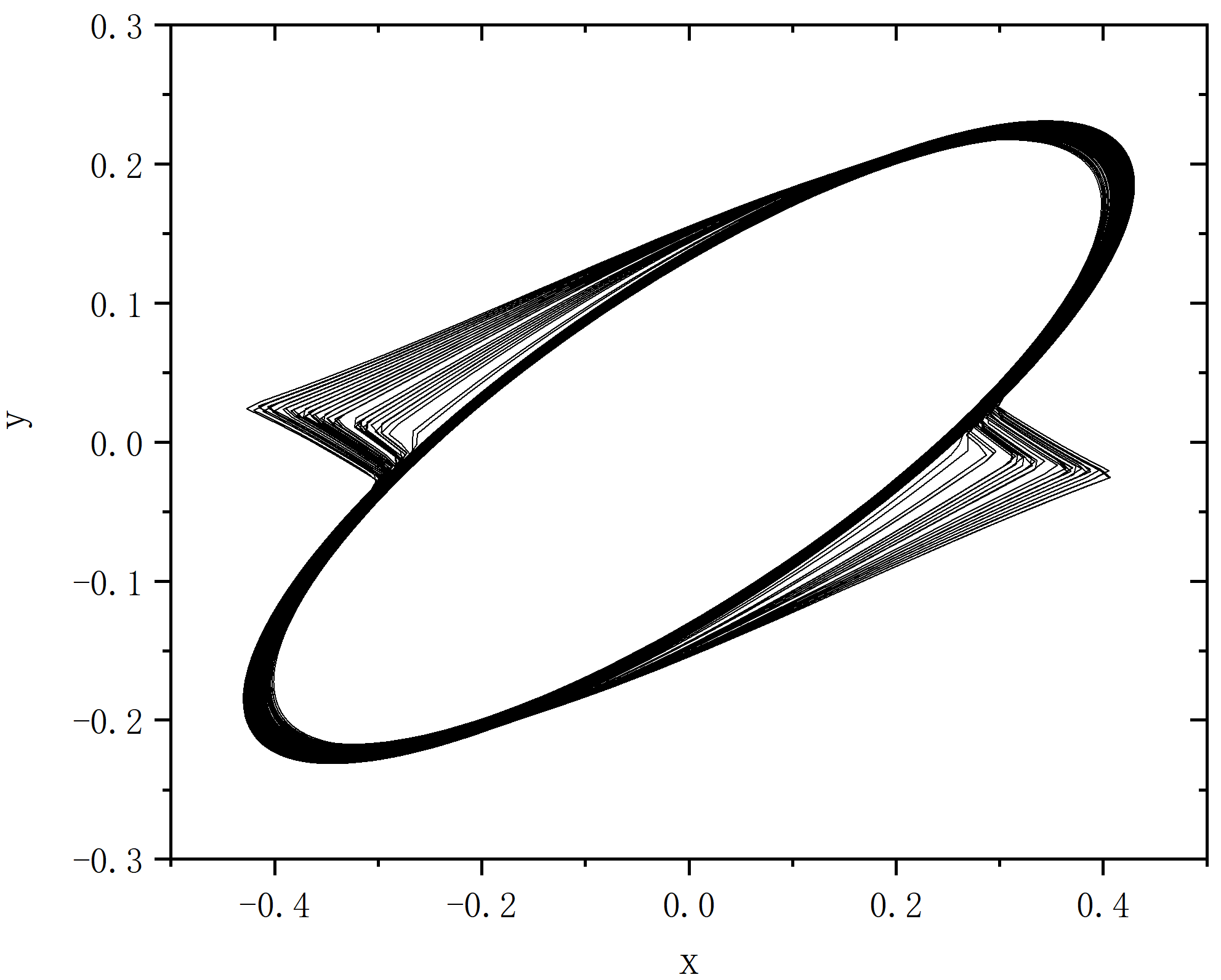
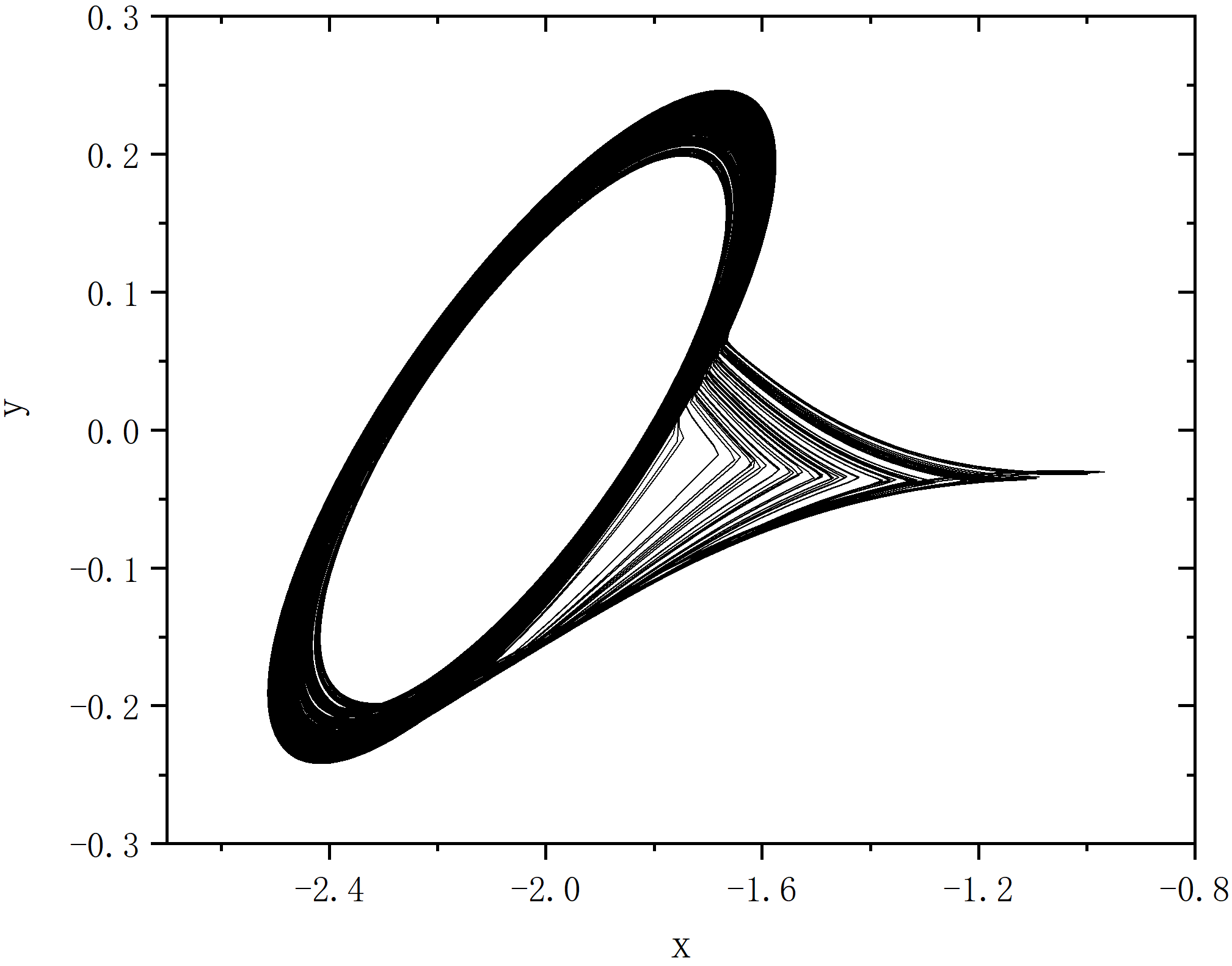
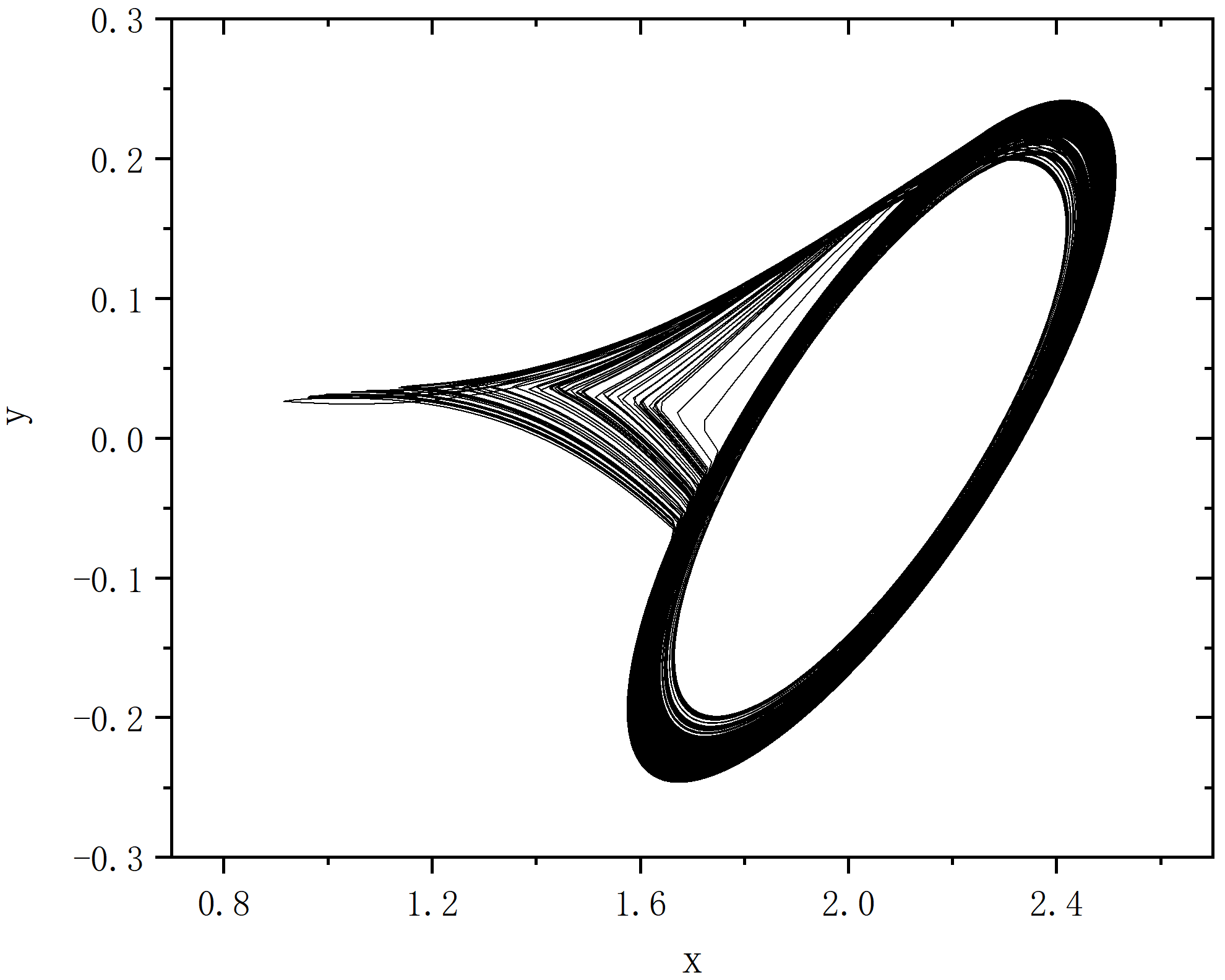
• ρ=1.5

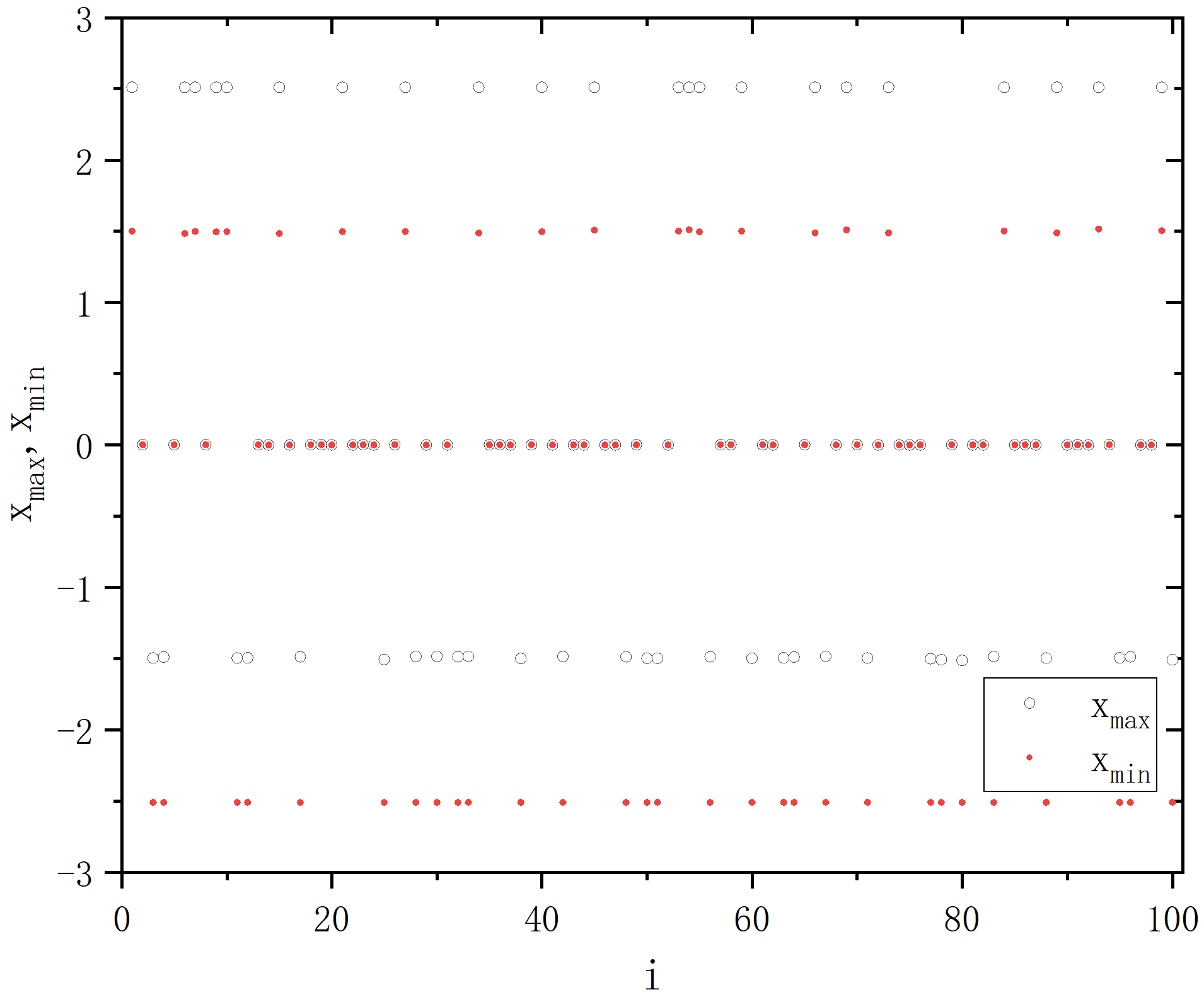
figure 8_A

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1450000,T_trans=1400000,N=3,M=100
    real :: x(M,N)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=2*x1-1.0
            x(i,2)=2*x2-1.0
            x(i,3)=2*x3-1.0
            write(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i)
        implicit none
        real :: xx(N),fx(N),coupling,gx
        integer :: t,i,j
        real :: a,b,c,cc,K,m0,m1
        a=10.0 !alpha
        b=1.47 !rho
        c=14.0 !delta
        K=0.03
        cc=1.0
        m0=-0.43
        m1=0.41
        coupling=0.0
        do j=1,M,1
            coupling=coupling+neighbour_matrix(i,j)*(x(j,2)-x(i,2))
        end do
        gx=m1*xx(1)+(1.0/2.0)*(m0-m1)*(abs(xx(1)+1.0)-abs(xx(1)-1.0))
        if(abs(xx(3))>=cc) then
            fx(1)=a*(xx(2)-gx)
        else if(abs(xx(3))<cc) then
            fx(1)=a*(xx(2)+gx)
        end if
        fx(2)=xx(1)-b*xx(2)+xx(3)+(K/real(M-1))*coupling
        fx(3)=-c*xx(2)
        return
    end subroutine fnf


    subroutine rk4(x)
        implicit none
        integer :: i
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour


end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j,counter
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_5.txt")
    open(42,file="t_x_50.txt")
    open(43,file="t_x_23.txt")
    open(44,file="t_x_95.txt")
    open(45,file="t_x_36.txt")
    open(46,file="t_x_61.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="error.txt")
    call neighbour()
    call x0
    U_max=-1000.0
    U_min=1000.0
    counter=1
    do t=1,MaxT,1
        call rk4(x)
        if(t>T_trans) then
            call U_max_min(x(:,1),U_max,U_min)
            write(40,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(41,*) (t-T_trans)*h,x(5,1),x(5,2),x(5,3)
            write(42,*) (t-T_trans)*h,x(50,1),x(50,2),x(50,3)
            write(43,*) (t-T_trans)*h,x(23,1),x(23,2),x(23,3)
            write(44,*) (t-T_trans)*h,x(95,1),x(95,2),x(95,3)
            write(45,*) (t-T_trans)*h,x(36,1),x(36,2),x(36,3)
            write(46,*) (t-T_trans)*h,x(61,1),x(61,2),x(61,3)
            !将相同的动力学模式放在一起
            do i=1,M,1
                data(i,t-T_trans,1) = x(i,1)
                data(i,t-T_trans,2) = x(i,2)
                data(i,t-T_trans,3) = x(i,3)
            end do
        end if
    end do
    do i=1,M,1
        write(30,*) i,U_max(i),U_min(i)
        do t=1,MaxT-T_trans,1
            if(U_max(i)>0.0.and.U_min(i)<0.0) then
                !B1
                if(mod(t,100)==0) then
                    write(20,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)<0.0.and.U_min(i)<0.0) then
                !B2
                if(mod(t,100)==0) then
                    write(21,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)>0.0.and.U_min(i)>0.0) then
                !B3
                if(mod(t,100)==0) then
                    write(22,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else
                write(60,*) "条件有误！"
            end if
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main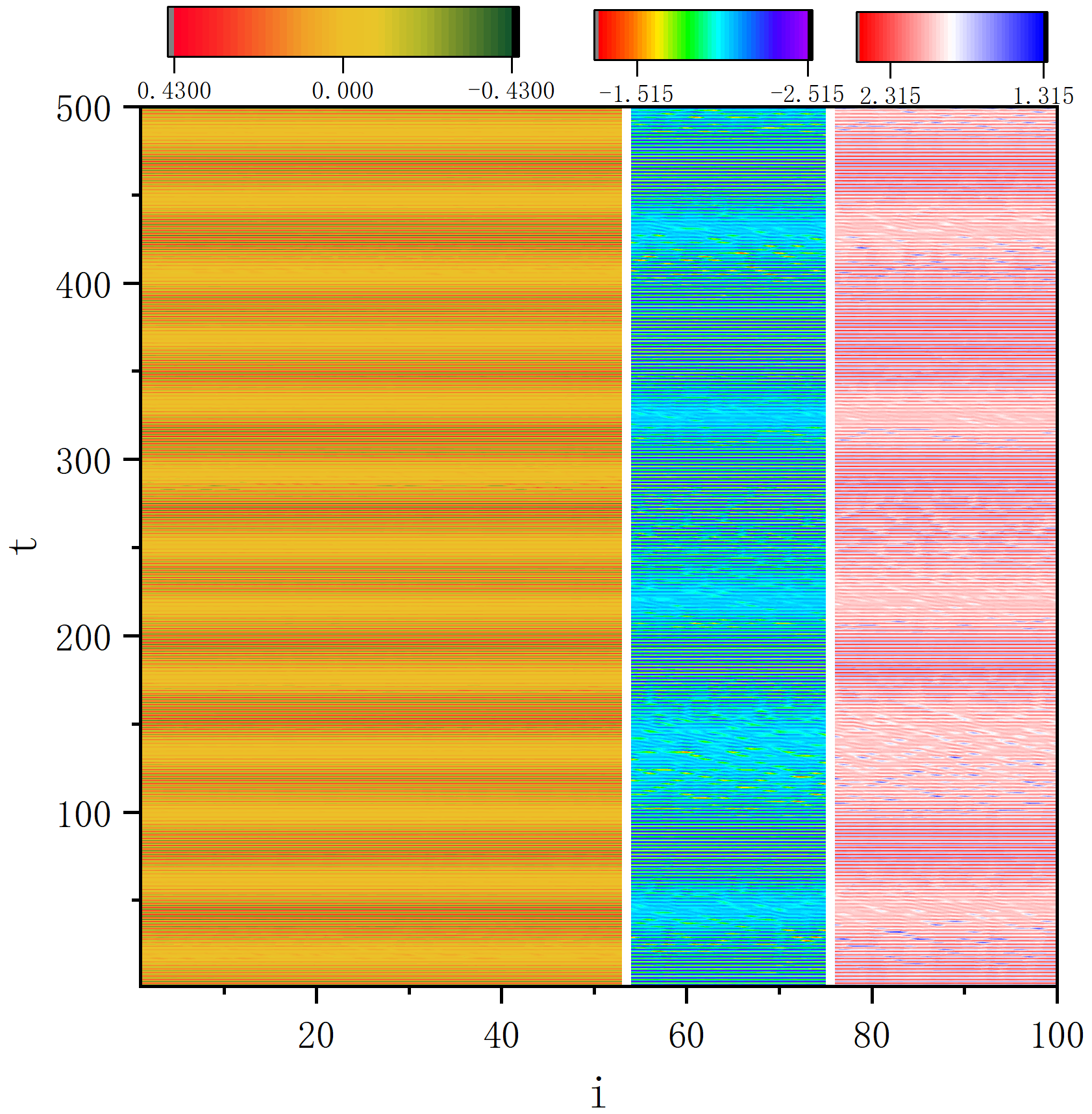

figure 8_B

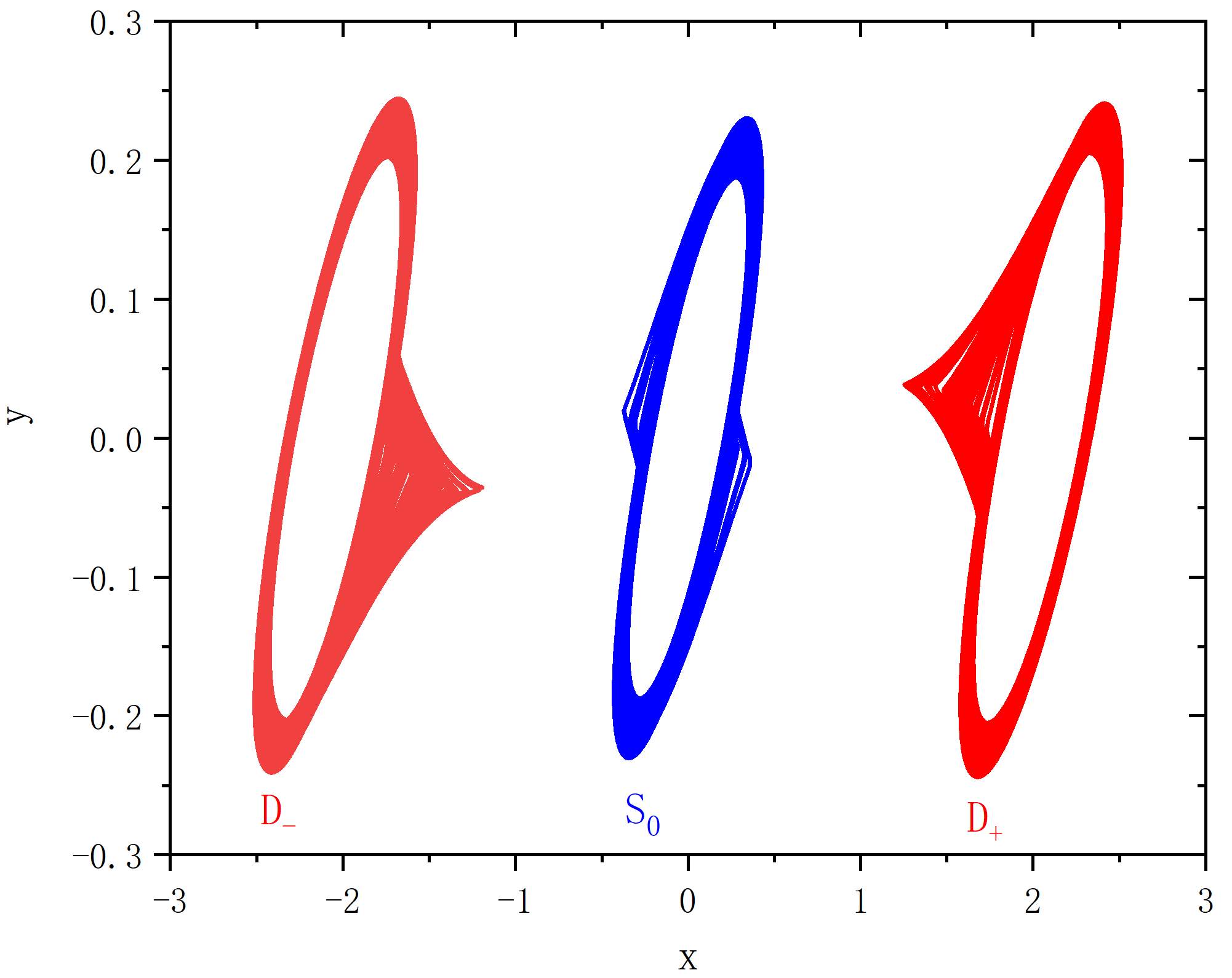
figure 8_C

module Lorenz
    implicit none
    real,parameter :: h=0.01
    integer,parameter :: MaxT=1950000,T_trans=1900000,N=3,M=100
    real :: x(M,N),f(MaxT)
    integer,allocatable :: neighbour_matrix(:,:)
contains

    subroutine x0()
        implicit none
        integer :: i
        real :: x1,x2,x3
        call random_seed()
        open(5,file="x0_y0_z0.txt")
        do i=1,M,1
            call random_number(x1)
            call random_number(x2)
            call random_number(x3)
            x(i,1)=2*x1-1.0
            x(i,2)=2*x2-1.0
            x(i,3)=2*x3-1.0
            write(5,*) x(i,1),x(i,2),x(i,3)
        end do
        close(5)
    end subroutine x0

    subroutine fnf(xx,fx,i,t)
        implicit none
        real :: xx(N),fx(N),coupling,gx
        integer :: t,i,j
        real :: a,b,c,cc,m0,m1,epsilon
        a=10.0 !alpha
        b=1.50 !rho
        c=14.0 !delta
        cc=1.0
        m0=-0.43
        m1=0.41
        epsilon=0.5
        gx=m1*xx(1)+(1.0/2.0)*(m0-m1)*(abs(xx(1)+1.0)-abs(xx(1)-1.0))
        if(abs(xx(3))>cc) then
            fx(1)=a*(xx(2)-gx)
        else if(abs(xx(3))<=cc) then
            fx(1)=a*(xx(2)+gx)
        end if
        fx(2)=xx(1)-b*xx(2)+xx(3)+epsilon*f(t)
        fx(3)=-c*xx(2)
        return
    end subroutine fnf


    subroutine rk4(x,t)
        implicit none
        integer :: i,t
        real :: x(M,N),xx(N),fx(N)
        real :: kx1(N),kx2(N),kx3(N),kx4(N)
        do i=1,M,1
            xx=x(i,:)
            call fnf(xx,fx,i,t)
            kx1=h*fx
            xx=x(i,:)+0.5*kx1
            call fnf(xx,fx,i,t)
            kx2=h*fx
            xx=x(i,:)+0.5*kx2
            call fnf(xx,fx,i,t)
            kx3=h*fx
            xx=x(i,:)+kx3
            call fnf(xx,fx,i,t)
            kx4=h*fx
            x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
        end do
        return
    end subroutine rk4

    !Umax与Umin
    subroutine U_max_min(xxx,U_max,U_min)
        implicit none
        real :: U_max(M),U_min(M),xxx(M)
        integer :: i
        do i=1,M,1
            if(U_max(i)<xxx(i)) then
                U_max(i)=xxx(i)
            end if
            if(U_min(i)>xxx(i)) then
                U_min(i)=xxx(i)
            end if
        end do
        return
    end subroutine U_max_min

    !建立网络结构
    subroutine neighbour()
        implicit none
        integer :: i,j,number
        allocate(neighbour_matrix(M,M))
        !初始化网络矩阵
        neighbour_matrix=0
        do i=1,M-1,1
            do j=i+1,M,1
                neighbour_matrix(i,j)=1
                neighbour_matrix(j,i)=1
            end do
        end do
        !输出矩阵
        do i=1,M,1
            do j=1,M,1
                write(10,"(I2)",advance='no') neighbour_matrix(i,j)
            end do
            write(10,*)
        end do
        return
    end subroutine neighbour

    !普通高斯白噪声
    subroutine gaussNoise()
        implicit none
        integer, parameter :: L = MaxT ! 生成噪声的长度
        real,parameter :: pi=3.1415926
        real :: noise(L)            ! 储存噪声的数组
        real :: mean = 0.0         ! 均值
        real :: std_dev = 0.01      ! 标准差
        integer :: seed = 1         ! 随机数种子
        integer :: i
        open(11,file="noise.txt")
        ! 生成噪声
        call random_seed()
        do i = 1, L
            call random_number(noise(i))
        end do
        do i=1,L-1
            noise(i) = mean + std_dev * sqrt(-2.0 * log(noise(i))) * cos(2.0 * pi * noise(i + 1))
        end do
        noise(L)=0.0
        ! 输出噪声
        do i = 1, L
            f(i)=noise(i)
            !write(11,*) i,noise(i)
        end do
        return
    end subroutine gaussNoise


end module Lorenz



program main
    use Lorenz
    implicit none
    integer :: t,i,j,counter
    real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
    open(10,file="neighbour_matrix.txt")
    open(20,file="i_t_x_B-.txt")
    open(21,file="i_t_x_B+.txt")
    open(22,file="i_t_x_B0.txt")
    open(30,file="xmax_xmin.txt")
    open(40,file="t_x_1.txt")
    open(41,file="t_x_5.txt")
    open(42,file="t_x_50.txt")
    open(43,file="t_x_23.txt")
    open(44,file="t_x_95.txt")
    open(45,file="t_x_36.txt")
    open(46,file="t_x_61.txt")
    open(50,file="t_x_1_data.txt")
    open(60,file="error.txt")
    call neighbour()
    call x0
    call gaussNoise()
    U_max=-1000.0
    U_min=1000.0
    counter=1
    do t=1,MaxT,1
        call rk4(x,t)
        if(t>T_trans) then
            call U_max_min(x(:,1),U_max,U_min)
            write(40,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
            write(41,*) (t-T_trans)*h,x(5,1),x(5,2),x(5,3)
            write(42,*) (t-T_trans)*h,x(50,1),x(50,2),x(50,3)
            write(43,*) (t-T_trans)*h,x(23,1),x(23,2),x(23,3)
            write(44,*) (t-T_trans)*h,x(95,1),x(95,2),x(95,3)
            write(45,*) (t-T_trans)*h,x(36,1),x(36,2),x(36,3)
            write(46,*) (t-T_trans)*h,x(61,1),x(61,2),x(61,3)
            !将相同的动力学模式放在一起
            do i=1,M,1
                data(i,t-T_trans,1) = x(i,1)
                data(i,t-T_trans,2) = x(i,2)
                data(i,t-T_trans,3) = x(i,3)
            end do
        end if
    end do
    do i=1,M,1
        write(30,*) i,U_max(i),U_min(i)
        do t=1,MaxT-T_trans,1
            if(U_max(i)>0.0.and.U_min(i)<0.0) then
                !B1
                if(mod(t,100)==0) then
                    write(20,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)<0.0.and.U_min(i)<0.0) then
                !B2
                if(mod(t,100)==0) then
                    write(21,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else if(U_max(i)>0.0.and.U_min(i)>0.0) then
                !B3
                if(mod(t,100)==0) then
                    write(22,*) i,t,data(i,t,1),data(i,t,2),data(i,t,3)
                end if
            else
                write(60,*) "条件有误！"
            end if
        end do
    end do
    close(10)
    close(20)
    close(30)
    close(40)
    deallocate(neighbour_matrix)
end program main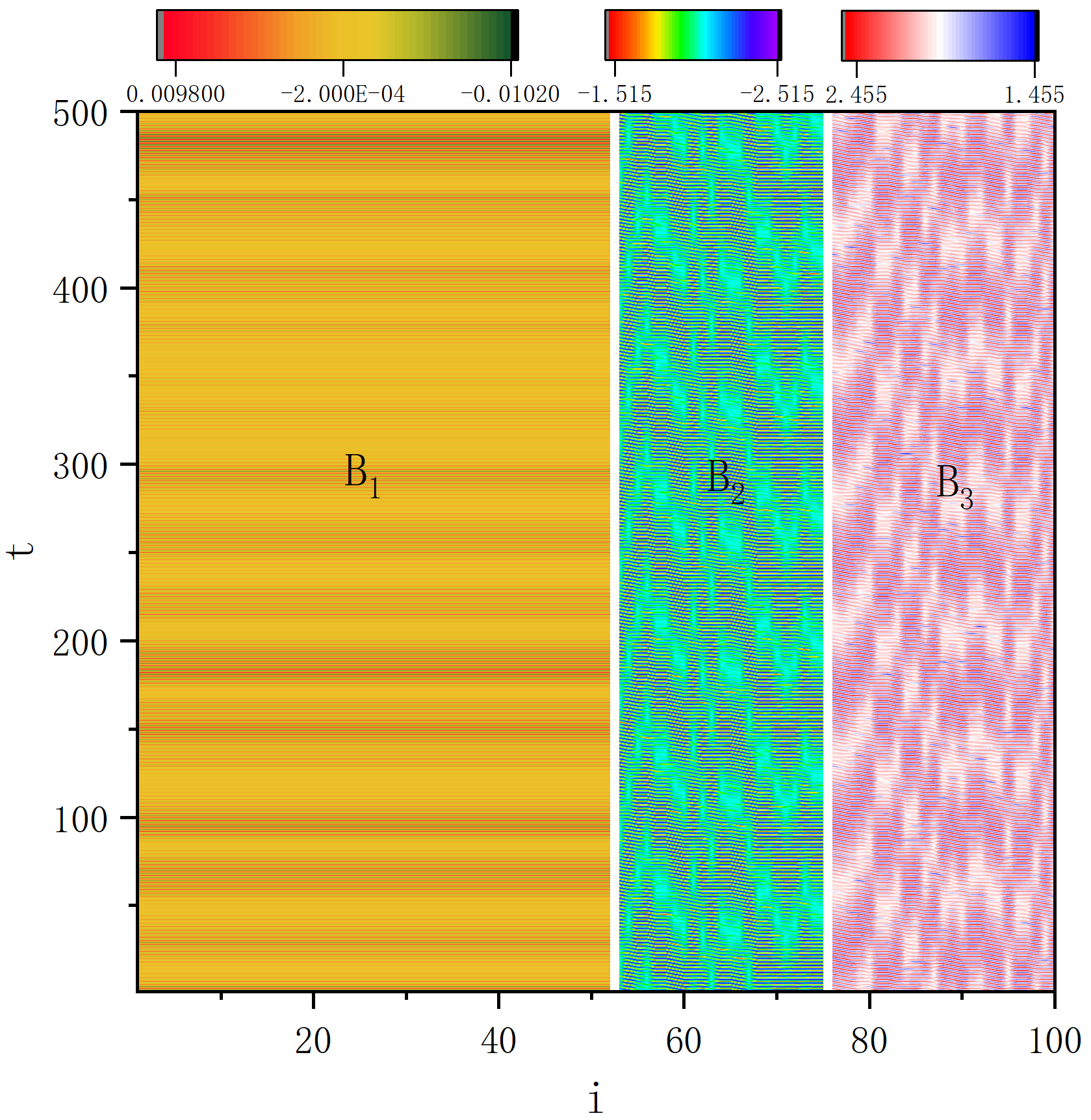

figure 8_D