Emergence of chimeras through induced multistability
阅读
下载地址:
Controlling chimera states in chaotic oscillator ensembles through linear augmentation.pdf
复现
单节点


figure 1
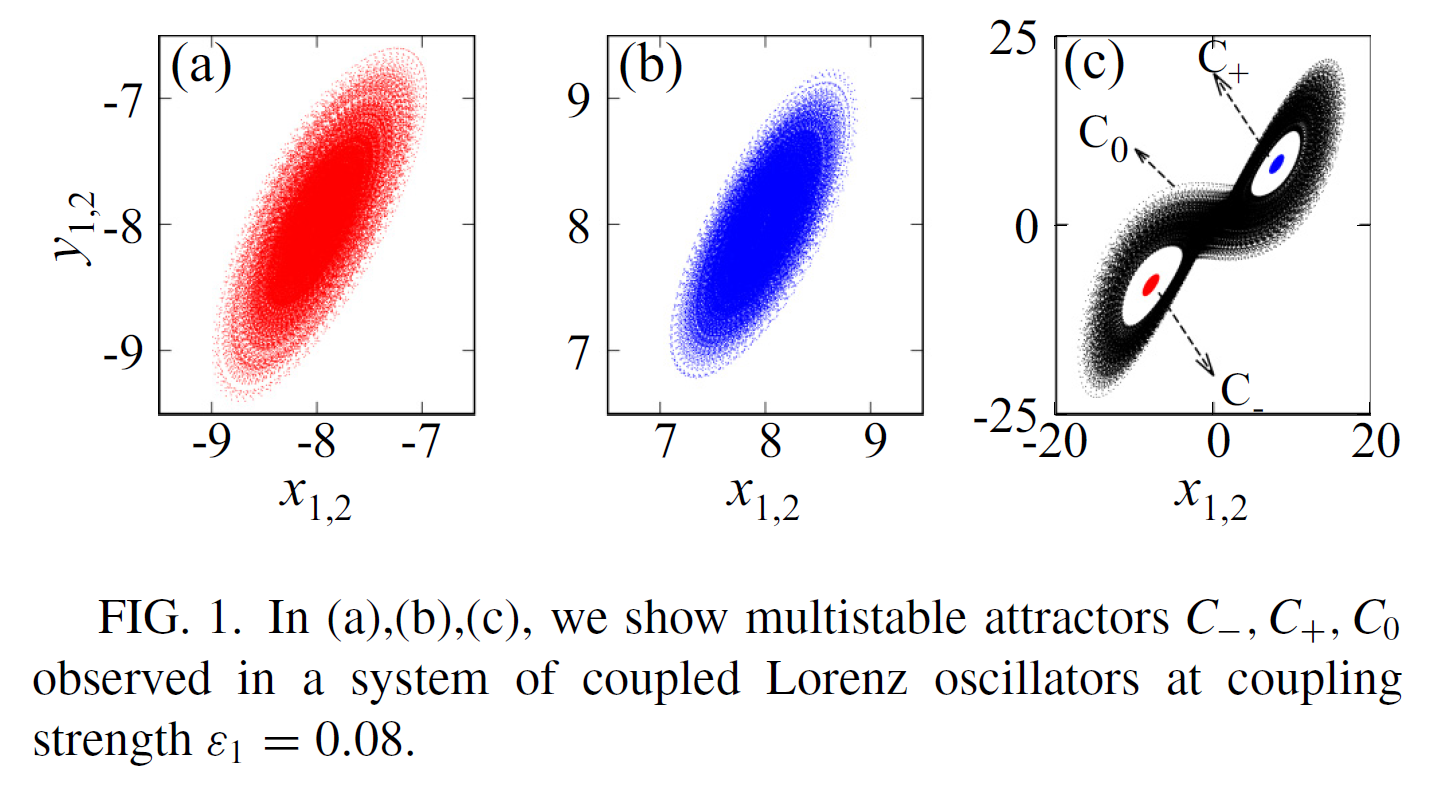
module Lorenz_control
implicit none
real,parameter :: h=0.01
integer,parameter :: MaxT=10530000,T_trans=10500000,N=3,M=2
real :: x(M,N)
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*100.0-100.0
x(i,2)=x2*100.0-100.0
x(i,3)=x3*100.0-100.0
write(5,*) x(i,1),x(i,2),x(i,3)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Umax与Umin
subroutine U_max_min(xxx,U_max,U_min)
implicit none
real :: U_max(M),U_min(M),xxx(M)
integer :: i
do i=1,M,1
if(U_max(i)<xxx(i)) then
U_max(i)=xxx(i)
end if
if(U_min(i)>xxx(i)) then
U_min(i)=xxx(i)
end if
end do
return
end subroutine U_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j
real :: U_max(M),U_min(M),data(M,MaxT-T_trans,3)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="t_x_1.txt")
open(40,file="t_x_2.txt")
call neighbour()
call x0
U_max=-1000.0
U_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call U_max_min(x(:,1),U_max,U_min)
write(30,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
write(40,*) (t-T_trans)*h,x(2,1),x(2,2),x(2,3)
end if
end do
do i=1,M,1
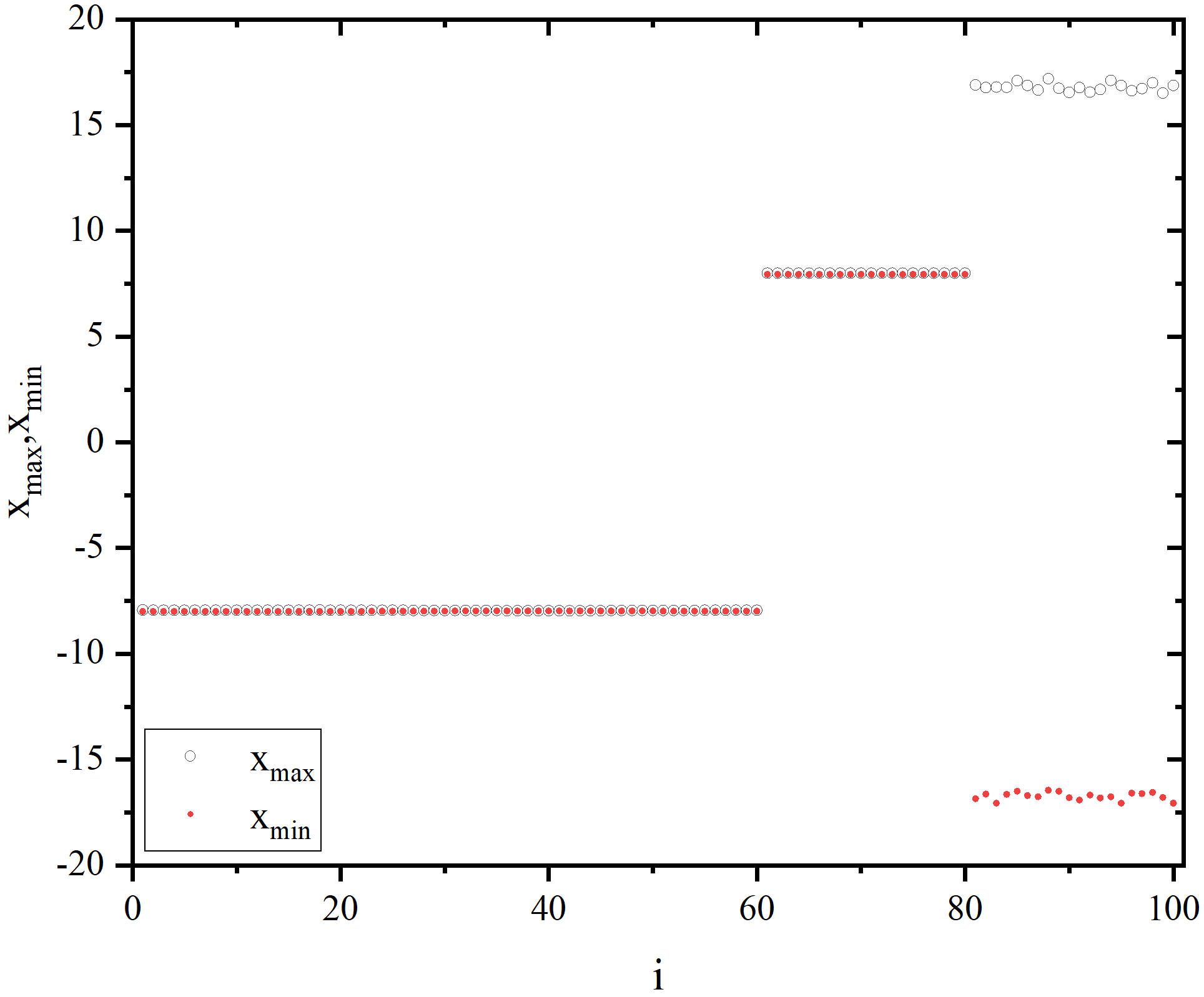
write(20,*) i,U_max(i),U_min(i)
end do
close(10)
close(20)
close(30)
close(40)
deallocate(neighbour_matrix)
end program mainfigure 1_A
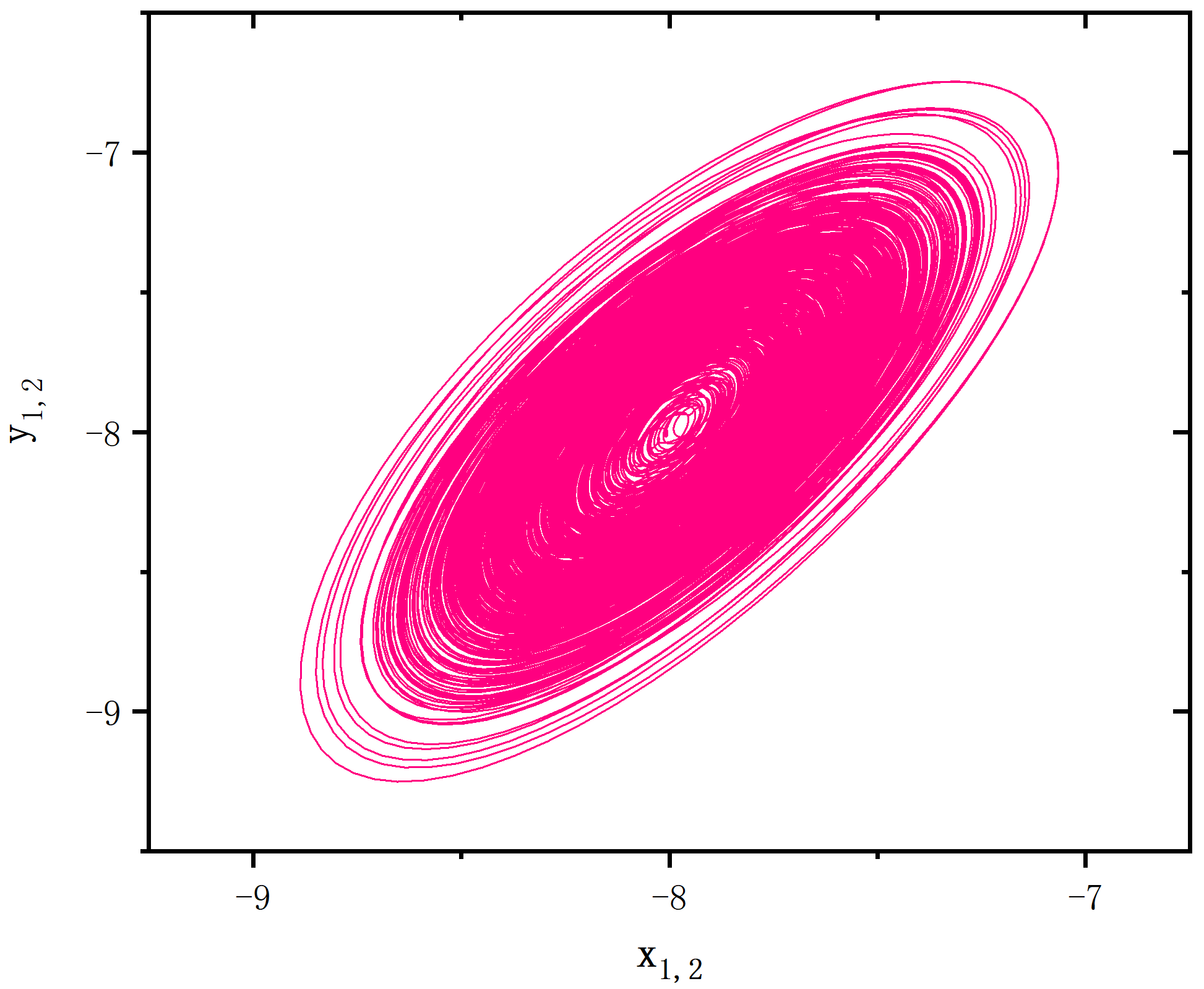
figure 1_B

figure 1_C

figure 2

module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=3,M=100
real :: x(M,N),phase(M)
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
write(5,*) x(i,1),x(i,2),x(i,3)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!phase_max与phase_min
subroutine phase_max_min(phase1,phase_max,phase_min)
implicit none
real :: phase_max(M),phase_min(M),phase1(M)
integer :: i
do i=1,M,1
if(phase_max(i)<phase1(i)) then
phase_max(i)=phase1(i)
end if
if(phase_min(i)>phase1(i)) then
phase_min(i)=phase1(i)
end if
end do
return
end subroutine phase_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,counter1,counter2,counter3,counter(M)
real :: X_max(M),X_min(M),phase_max(M),phase_min(M),data_x(M,MaxT-T_trans-50000,3),data_phase(M,MaxT-T_trans-50000),omega(M)
real,allocatable :: data_x_G1(:,:,:),data_x_G2(:,:,:),data_x_G3(:,:,:)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="phaseMax_phaseMin.txt")
open(50,file="i_t_x.txt")
open(51,file="i_t_x_load.txt")
open(60,file="i_500_x.txt")
open(70,file="i_500_phase.txt")
open(80,file="i_t_phase.txt")
open(81,file="i_t_x_G_.txt")
open(82,file="i_t_x_G+.txt")
open(83,file="i_t_x_G0.txt")
open(84,file="i_t_phase_G_.txt")
open(85,file="i_t_phase_G+.txt")
open(86,file="i_t_phase_G0.txt")
open(90,file="i_omega.txt")
open(100,file="error.txt")
open(110,file="phase_1.txt")
open(111,file="phase_2.txt")
open(120,file="t_x_1.txt")
call neighbour()
100 call x0
X_max=-1000.0
X_min=1000.0
counter1=0
counter2=0
counter3=0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
!x的时空斑图
if((t-T_trans)*h>500) then
do i=1,M,1
data_x(i,t-T_trans-50000,1) = x(i,1)
data_x(i,t-T_trans-50000,2) = x(i,2)
data_x(i,t-T_trans-50000,3) = x(i,3)
if(mod(t,100)==0) then
write(50,*) i,(t-T_trans)*h,x(i,1),x(i,2),x(i,3)
end if
end do
end if
end if
end do
do i=1,M,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
counter1=counter1+1
do t=1,MaxT-T_trans-50000,1
!G_
if(mod(t,100)==0) then
write(81,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
end if
end do
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
counter2=counter2+1
do t=1,MaxT-T_trans-50000,1
!G+
if(mod(t,100)==0) then
write(82,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
end if
end do
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
counter3=counter3+1
do t=1,MaxT-T_trans-50000,1
!G0
if(mod(t,100)==0) then
write(83,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
end if
end do
else
write(100,*) "区分data_x条件有误!"
end if
end do
!时空斑图秩序化
if(counter1/=0.and.counter2/=0.and.counter3/=0) then
write(*,*) counter1,counter2,counter3
allocate(data_x_G1(counter1,MaxT-T_trans-50000,3))
allocate(data_x_G2(counter2,MaxT-T_trans-50000,3))
allocate(data_x_G3(counter3,MaxT-T_trans-50000,3))
else
goto 100
end if
counter1=0
counter2=0
counter3=0
do i=1,M,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G_
counter1=counter1+1
do t=1,MaxT-T_trans-50000,1
data_x_G1(counter1,t,1)=data_x(i,t,1)
data_x_G1(counter1,t,2)=data_x(i,t,2)
data_x_G1(counter1,t,3)=data_x(i,t,3)
end do
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
counter2=counter2+1
do t=1,MaxT-T_trans-50000,1
data_x_G2(counter2,t,1)=data_x(i,t,1)
data_x_G2(counter2,t,2)=data_x(i,t,2)
data_x_G2(counter2,t,3)=data_x(i,t,3)
end do
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
counter3=counter3+1
do t=1,MaxT-T_trans-50000,1
data_x_G3(counter3,t,1)=data_x(i,t,1)
data_x_G3(counter3,t,2)=data_x(i,t,2)
data_x_G3(counter3,t,3)=data_x(i,t,3)
end do
else
write(100,*) "区分data_x条件有误!"
end if
end do
!整合时空斑图
data_x=0
do i=1,counter1,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G1(i,t,1)
data_x(i,t,2)=data_x_G1(i,t,2)
data_x(i,t,3)=data_x_G1(i,t,3)
end do
end do
do i=counter1+1,counter1+counter2,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G2(i-counter1,t,1)
data_x(i,t,2)=data_x_G2(i-counter1,t,2)
data_x(i,t,3)=data_x_G2(i-counter1,t,3)
end do
end do
do i=counter1+counter2+1,M,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G3(i-counter1-counter2,t,1)
data_x(i,t,2)=data_x_G3(i-counter1-counter2,t,2)
data_x(i,t,3)=data_x_G3(i-counter1-counter2,t,3)
end do
end do
do i=1,M,1
do t=50000,MaxT-T_trans-1,1
write(120,*) t*h,data_x(10,t-50000+1,1),data_x(10,t-50000+1,2),data_x(10,t-50000+1,3)
phase=0
! 计算相位角
if (data_x(i,t-50000+1,1) == 0.0 .and. data_x(i,t-50000+1,2) == 0.0) then
phase(i) = 0.0
else
phase(i) = atan2(data_x(i,t-50000+1,2),data_x(i,t-50000+1,1))
if (phase(i) < 0.0) then
phase(i) = phase(i) + 2.0 * atan(1.0) * 4.0
endif
endif
data_phase(i,t-50000+1) = phase(i)
if(t==50000) then
!x的快照
write(60,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
write(70,*) i,t*h,data_phase(i,t-50000+1)
end if
if(mod(t,100)==0) then
write(51,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
write(80,*) i,t*h,data_phase(i,t-50000+1)
end if
end do
end do
X_max=-1000.0
X_min=1000.0
phase_max=-1000.0
phase_min=1000.0
do t=50000,MaxT-T_trans-1,1
write(110,*) t*h,data_phase(10,t-50000+1)
write(111,*) t*h,data_phase(2,t-50000+1)
call phase_max_min(data_phase(:,t-50000+1),phase_max,phase_min)
call X_max_min(data_x(:,t-50000+1,1),X_max,X_min)
end do
!omega_i
counter=0 !max_number
do i=1,M,1
write(20,*) i,X_max(i),X_min(i)
write(30,*) i,phase_max(i),phase_min(i)
do t=1,MaxT-T_trans-50000-2,1
if(data_x(i,t+1,1)>data_x(i,t,1).and.data_x(i,t+1,1)>data_x(i,t+2,1)) then
counter(i)=counter(i)+1
end if
end do
end do
do i=1,M,1
omega(i)=(2.0*PI*counter(i))/((MaxT-T_trans-50000-2)*h)
write(90,*) i,omega(i)
end do
close(10)
close(20)
close(30)
close(50)
close(60)
close(70)
close(80)
close(81)
close(82)
close(83)
close(84)
close(85)
close(86)
close(100)
deallocate(neighbour_matrix)
deallocate(data_x_G1)
deallocate(data_x_G2)
deallocate(data_x_G3)
end program mainfigure 2_A
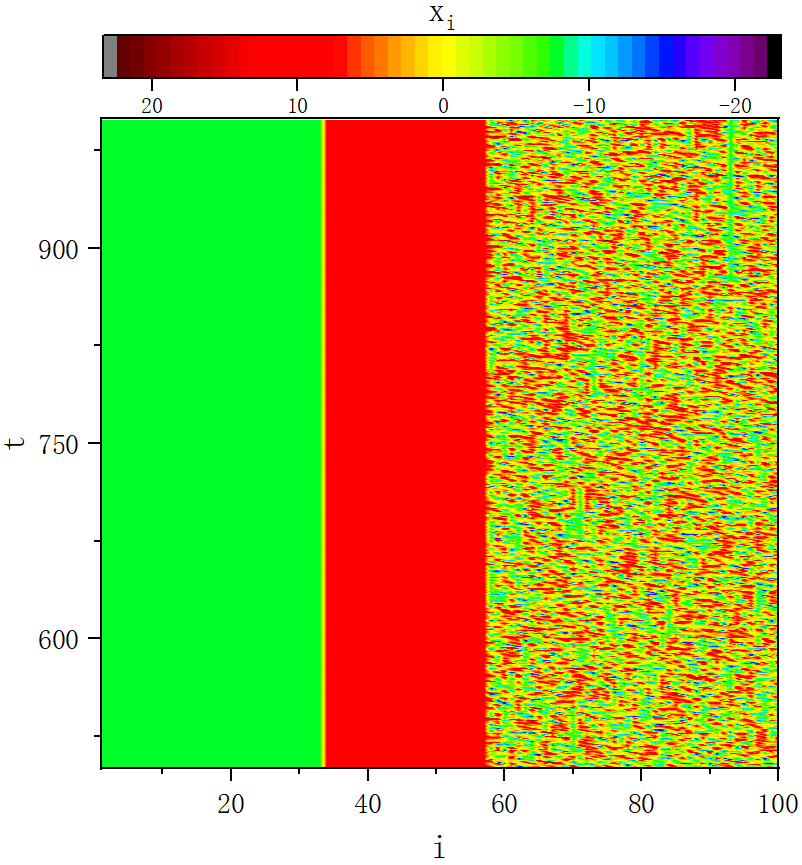
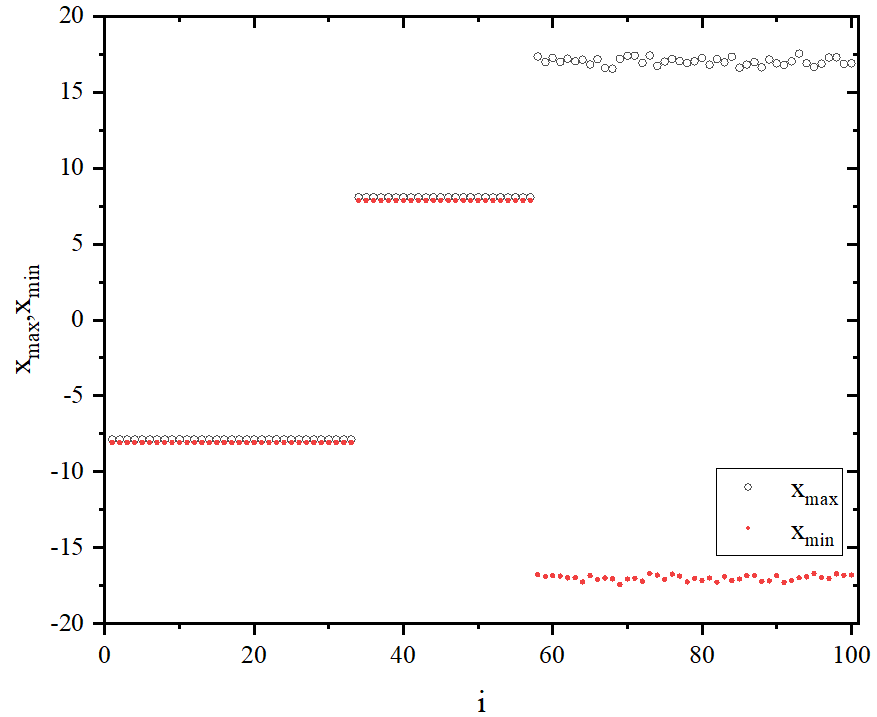
figure 2_B
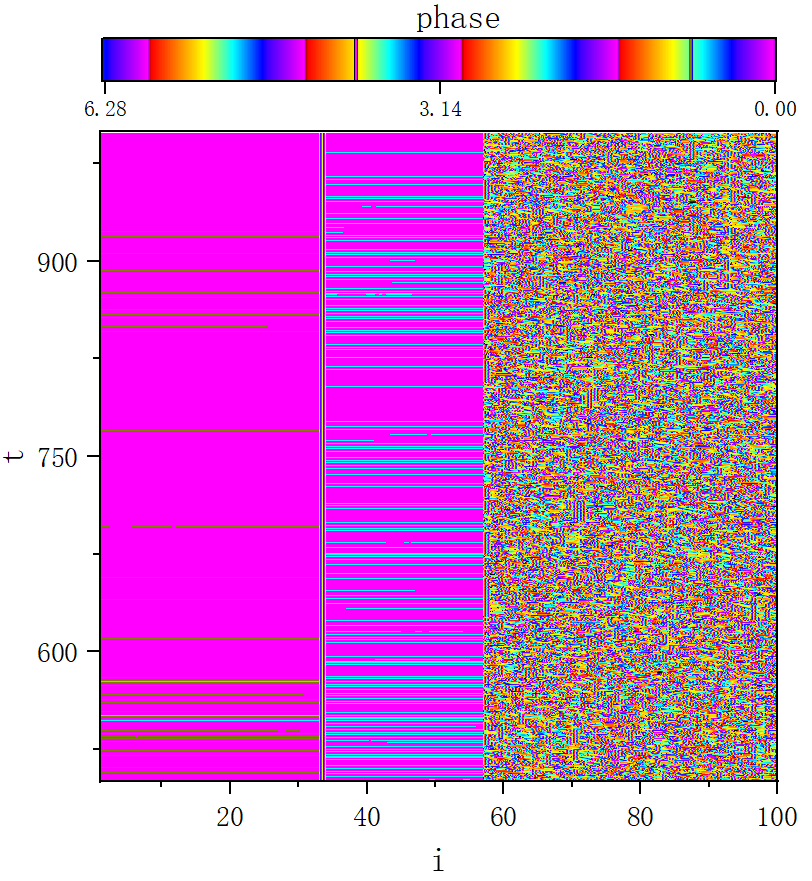
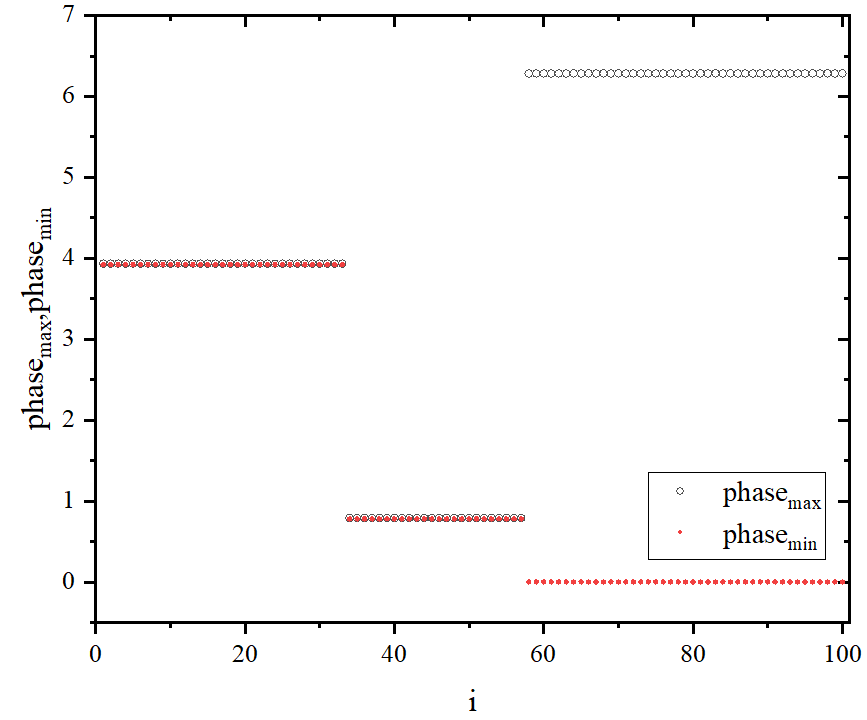
figure 2_C
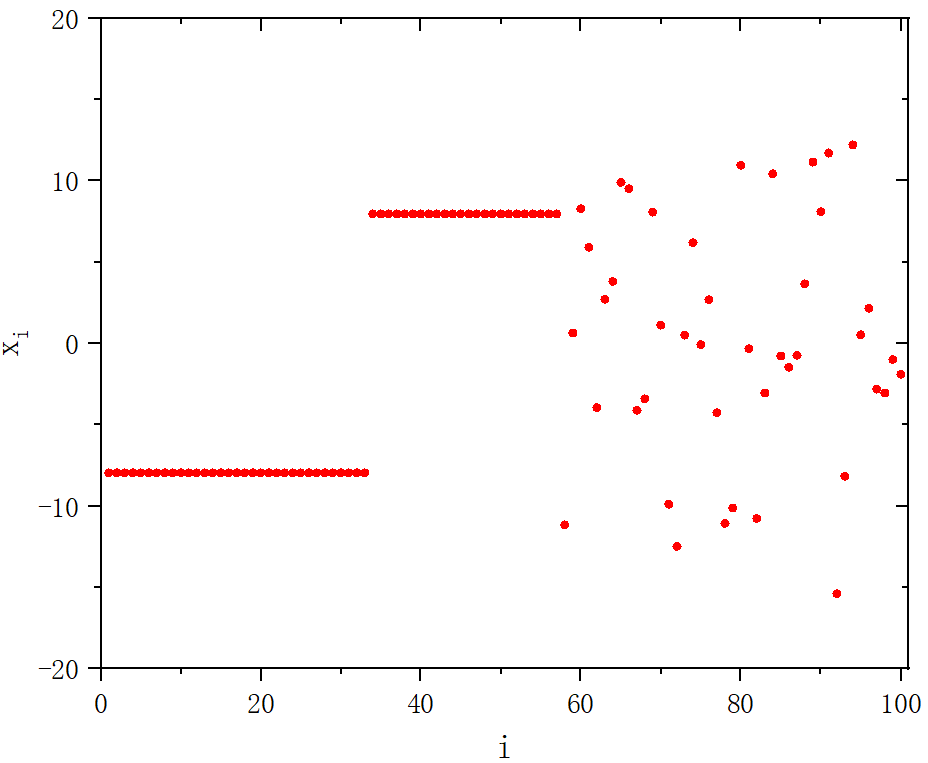
figure 2_D
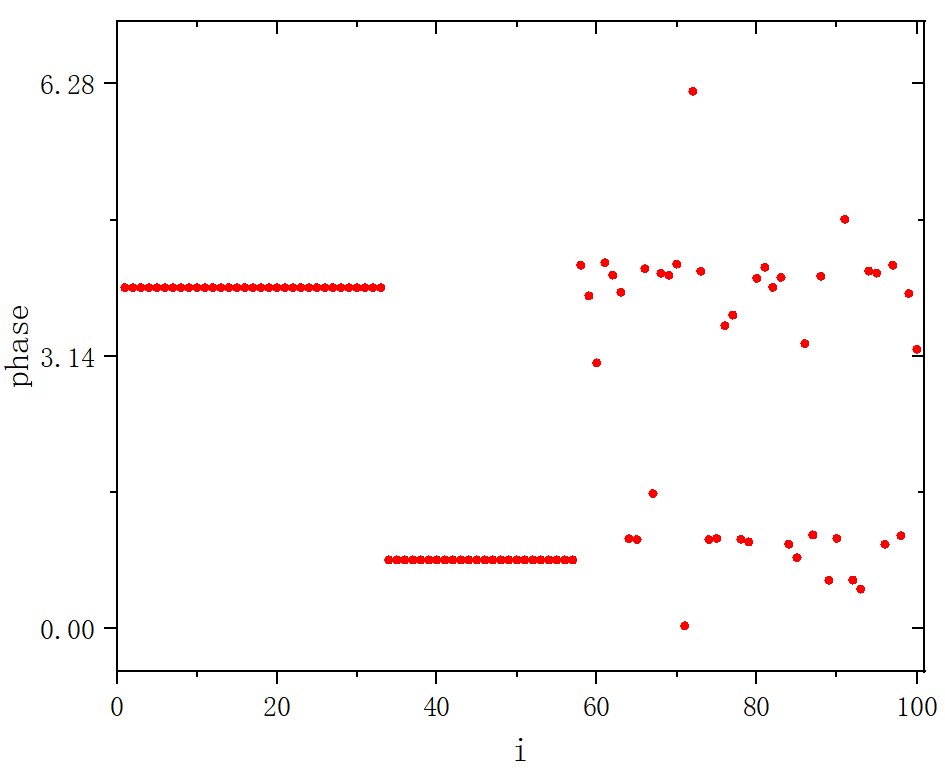
figure 2_E
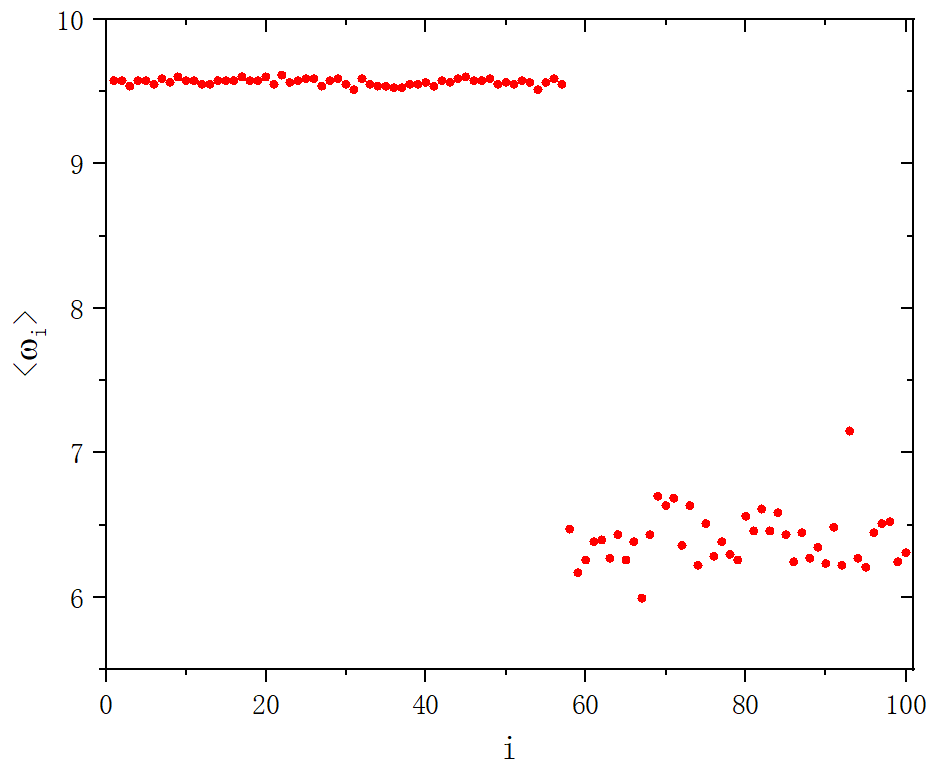
figure3
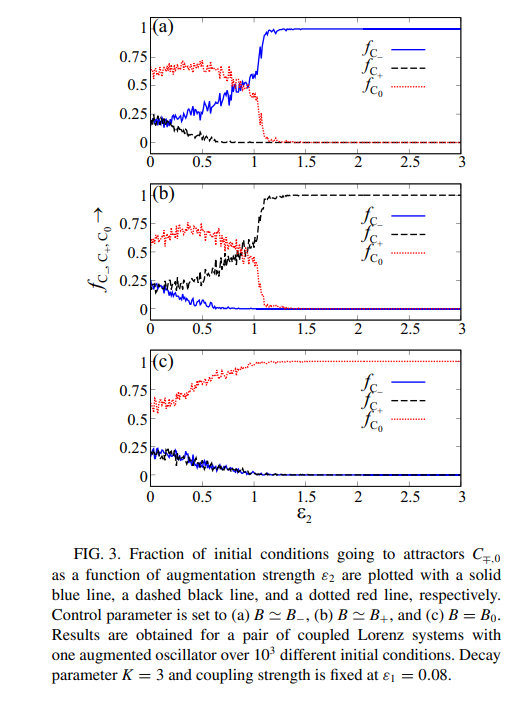
figure 3_A
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=2,cycle_number=500
real :: x(M,N),epsilon_2,E(M)=1
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
x(i,4)=0.0
write(5,*) x(i,1),x(i,2),x(i,3),x(i,4)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,BB,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
!B_
BB=-7.9666
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB)
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,counter1,counter2,counter3
real :: X_max(M),X_min(M)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="t_x_1.txt")
open(40,file="t_x_2.txt")
open(50,file="epsilon2_f.txt")
call neighbour()
do i=1,50,1
epsilon_2=i*0.01
counter1=0 !B_
counter2=0 !B+
counter3=0 !B0
do j=1,cycle_number,1
call x0
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
! write(30,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
! write(40,*) (t-T_trans)*h,x(2,1),x(2,2),x(2,3)
end if
end do
do jj=1,M,1
if(abs(X_max(jj)-X_min(jj))<5.0.and.X_max(jj)<0) then
counter1=counter1+1
else if(abs(X_max(jj)-X_min(jj))<5.0.and.X_min(jj)>0) then
counter2=counter2+1
else
counter3=counter3+1
end if
end do
end do
write(50,*) epsilon_2,counter1/real(cycle_number*M),counter2/real(cycle_number*M),counter3/real(cycle_number*M)
end do
close(10)
close(20)
close(30)
close(40)
close(50)
deallocate(neighbour_matrix)
end program main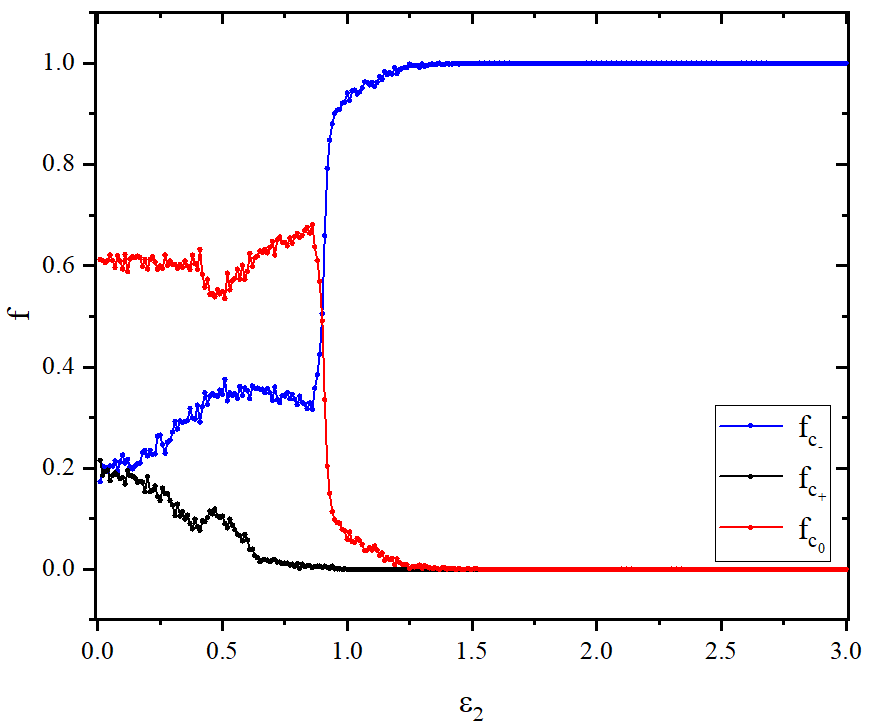
figure 3_B
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=2,cycle_number=500
real :: x(M,N),epsilon_2,E(M)=1
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
x(i,4)=0.0
write(5,*) x(i,1),x(i,2),x(i,3),x(i,4)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,BB,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
!B_
BB=7.9666
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB)
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,counter1,counter2,counter3
real :: X_max(M),X_min(M)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="t_x_1.txt")
open(40,file="t_x_2.txt")
open(50,file="epsilon2_f.txt")
call neighbour()
do i=1,50,1
epsilon_2=i*0.01
counter1=0 !B_
counter2=0 !B+
counter3=0 !B0
do j=1,cycle_number,1
call x0
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
! write(30,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
! write(40,*) (t-T_trans)*h,x(2,1),x(2,2),x(2,3)
end if
end do
do jj=1,M,1
if(abs(X_max(jj)-X_min(jj))<5.0.and.X_max(jj)<0) then
counter1=counter1+1
else if(abs(X_max(jj)-X_min(jj))<5.0.and.X_min(jj)>0) then
counter2=counter2+1
else
counter3=counter3+1
end if
end do
end do
write(*,*) epsilon_2,counter1/real(cycle_number*M),counter2/real(cycle_number*M),counter3/real(cycle_number*M)
write(50,*) epsilon_2,counter1/real(cycle_number*M),counter2/real(cycle_number*M),counter3/real(cycle_number*M)
end do
close(10)
close(20)
close(30)
close(40)
close(50)
deallocate(neighbour_matrix)
end program main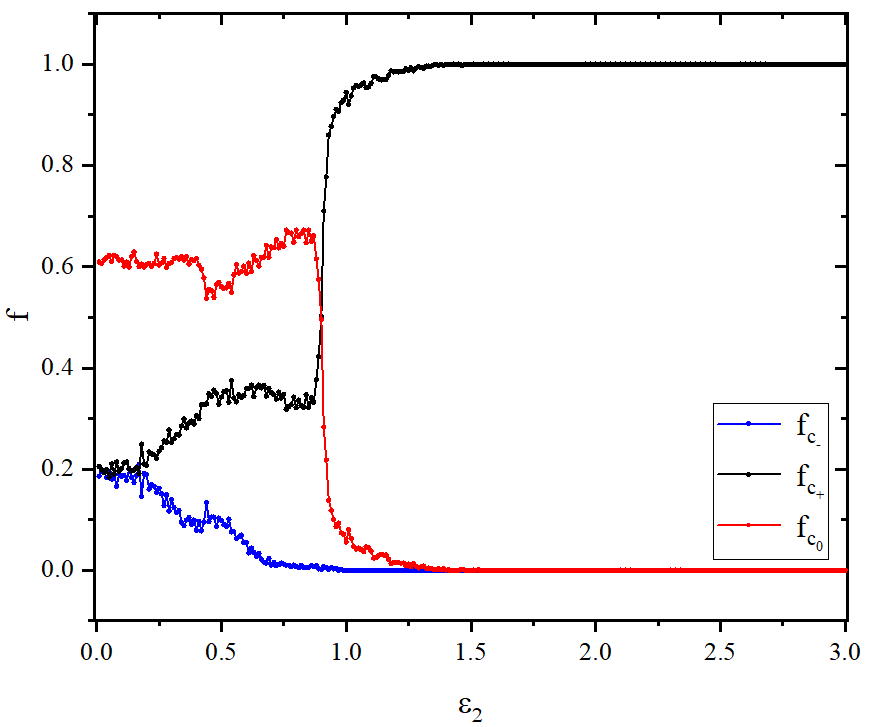
figure 3_C
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=2,cycle_number=500
real :: x(M,N),epsilon_2,E(M)=1
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
x(i,4)=0.0
write(5,*) x(i,1),x(i,2),x(i,3),x(i,4)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,BB,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
!B_
BB=0.0
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB)
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,counter1,counter2,counter3
real :: X_max(M),X_min(M)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="t_x_1.txt")
open(40,file="t_x_2.txt")
open(50,file="epsilon2_f.txt")
call neighbour()
do i=1,50,1
epsilon_2=i*0.01
counter1=0 !B_
counter2=0 !B+
counter3=0 !B0
do j=1,cycle_number,1
call x0
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
! write(30,*) (t-T_trans)*h,x(1,1),x(1,2),x(1,3)
! write(40,*) (t-T_trans)*h,x(2,1),x(2,2),x(2,3)
end if
end do
do jj=1,M,1
if(abs(X_max(jj)-X_min(jj))<5.0.and.X_max(jj)<0) then
counter1=counter1+1
else if(abs(X_max(jj)-X_min(jj))<5.0.and.X_min(jj)>0) then
counter2=counter2+1
else
counter3=counter3+1
end if
end do
end do
write(*,*) epsilon_2,counter1/real(cycle_number*M),counter2/real(cycle_number*M),counter3/real(cycle_number*M)
write(50,*) epsilon_2,counter1/real(cycle_number*M),counter2/real(cycle_number*M),counter3/real(cycle_number*M)
end do
close(10)
close(20)
close(30)
close(40)
close(50)
deallocate(neighbour_matrix)
end program main
figure 4
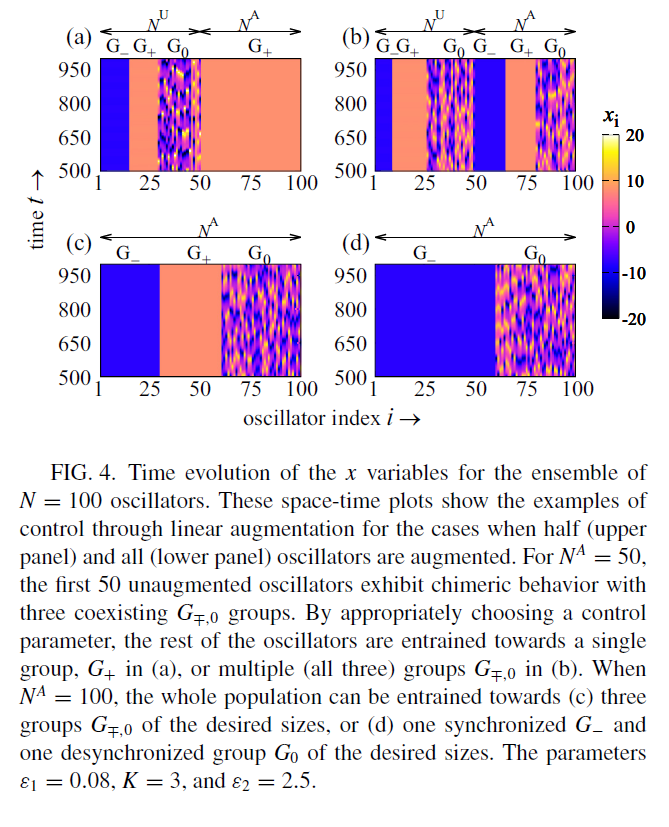
figure 4_A
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=100
real :: x(M,N),epsilon_2,E(M)=0
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
x(i,4)=0.0
write(5,*) x(i,1),x(i,2),x(i,3),x(i,4)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,BB,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
!B_
BB=7.9666
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB)
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,counter1,counter2,counter3
real :: X_max(M),X_min(M),data_x(M,MaxT-T_trans-50000,3)
real,allocatable :: data_x_G1(:,:,:),data_x_G2(:,:,:),data_x_G3(:,:,:)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="i_t_x.txt")
open(40,file="t_x_2.txt")
open(100,file="error.txt")
call neighbour()
E(51:100)=1
epsilon_2=2.5
counter1=0 !B_
counter2=0 !B+
counter3=0 !B0
call x0
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
!x的时空斑图
if((t-T_trans)*h>500) then
do i=1,M,1
data_x(i,t-T_trans-50000,1) = x(i,1)
data_x(i,t-T_trans-50000,2) = x(i,2)
data_x(i,t-T_trans-50000,3) = x(i,3)
end do
end if
end if
end do
do i=1,M/2,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
counter1=counter1+1
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
counter2=counter2+1
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
counter3=counter3+1
else
write(100,*) "1_区分data_x条件有误!"
end if
end do
!时空斑图秩序化
allocate(data_x_G1(counter1,MaxT-T_trans-50000,3))
allocate(data_x_G2(counter2,MaxT-T_trans-50000,3))
allocate(data_x_G3(counter3,MaxT-T_trans-50000,3))
counter1=0
counter2=0
counter3=0
do i=1,M/2,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G_
counter1=counter1+1
do t=1,MaxT-T_trans-50000,1
data_x_G1(counter1,t,1)=data_x(i,t,1)
data_x_G1(counter1,t,2)=data_x(i,t,2)
data_x_G1(counter1,t,3)=data_x(i,t,3)
end do
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
counter2=counter2+1
do t=1,MaxT-T_trans-50000,1
data_x_G2(counter2,t,1)=data_x(i,t,1)
data_x_G2(counter2,t,2)=data_x(i,t,2)
data_x_G2(counter2,t,3)=data_x(i,t,3)
end do
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
counter3=counter3+1
do t=1,MaxT-T_trans-50000,1
data_x_G3(counter3,t,1)=data_x(i,t,1)
data_x_G3(counter3,t,2)=data_x(i,t,2)
data_x_G3(counter3,t,3)=data_x(i,t,3)
end do
else
write(100,*) "2_区分data_x条件有误!"
end if
end do
!整合时空斑图
do i=1,counter1,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G1(i,t,1)
data_x(i,t,2)=data_x_G1(i,t,2)
data_x(i,t,3)=data_x_G1(i,t,3)
end do
end do
do i=counter1+1,counter1+counter2,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G2(i-counter1,t,1)
data_x(i,t,2)=data_x_G2(i-counter1,t,2)
data_x(i,t,3)=data_x_G2(i-counter1,t,3)
end do
end do
do i=counter1+counter2+1,M/2,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G3(i-counter1-counter2,t,1)
data_x(i,t,2)=data_x_G3(i-counter1-counter2,t,2)
data_x(i,t,3)=data_x_G3(i-counter1-counter2,t,3)
end do
end do
X_max=-1000.0
X_min=1000.0
do t=50000,MaxT-T_trans,1
call X_max_min(data_x(:,t-50000+1,1),X_max,X_min)
end do
do i=1,M,1
write(20,*) i,X_max(i),X_min(i)
end do
do i=1,M,1
do t=1,MaxT-T_trans-50000,1
if(mod(t,100)==0) then
write(30,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
end if
end do
end do
close(10)
close(20)
close(30)
close(40)
deallocate(data_x_G1)
deallocate(data_x_G2)
deallocate(data_x_G3)
deallocate(neighbour_matrix)
end program main
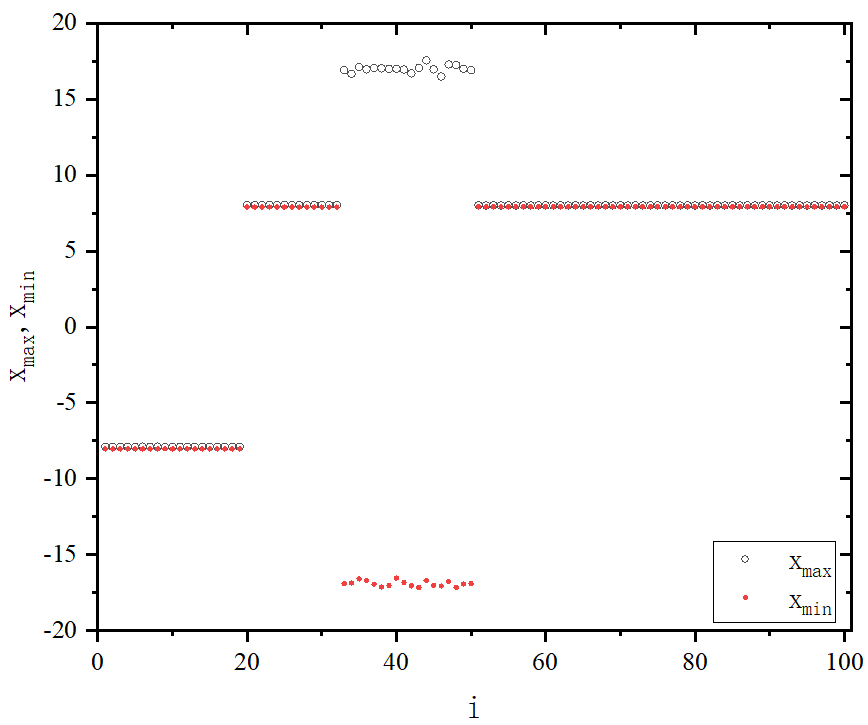
figure 4_B
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=100
real :: x(M,N),epsilon_2,E(M)=0,BB(M)=0.0
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
x(i,4)=0.0
write(5,*) x(i,1),x(i,2),x(i,3),x(i,4)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB(i))
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,counter1,counter2,counter3
real :: X_max(M),X_min(M),data_x(M,MaxT-T_trans-50000,3)
real,allocatable :: data_x_G1(:,:,:),data_x_G2(:,:,:),data_x_G3(:,:,:)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="i_t_x.txt")
open(40,file="t_x_2.txt")
open(100,file="error.txt")
call neighbour()
E(51:100)=1
BB(51:65)=-7.9666
BB(66:80)=7.9666
BB(81:100)=0.0
epsilon_2=2.5
counter1=0 !B_
counter2=0 !B+
counter3=0 !B0
call x0
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
!x的时空斑图
if((t-T_trans)*h>500) then
do i=1,M,1
data_x(i,t-T_trans-50000,1) = x(i,1)
data_x(i,t-T_trans-50000,2) = x(i,2)
data_x(i,t-T_trans-50000,3) = x(i,3)
end do
end if
end if
end do
do i=1,M/2,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
counter1=counter1+1
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
counter2=counter2+1
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
counter3=counter3+1
else
write(100,*) "1_区分data_x条件有误!"
end if
end do
!时空斑图秩序化
allocate(data_x_G1(counter1,MaxT-T_trans-50000,3))
allocate(data_x_G2(counter2,MaxT-T_trans-50000,3))
allocate(data_x_G3(counter3,MaxT-T_trans-50000,3))
counter1=0
counter2=0
counter3=0
do i=1,M/2,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G_
counter1=counter1+1
do t=1,MaxT-T_trans-50000,1
data_x_G1(counter1,t,1)=data_x(i,t,1)
data_x_G1(counter1,t,2)=data_x(i,t,2)
data_x_G1(counter1,t,3)=data_x(i,t,3)
end do
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
counter2=counter2+1
do t=1,MaxT-T_trans-50000,1
data_x_G2(counter2,t,1)=data_x(i,t,1)
data_x_G2(counter2,t,2)=data_x(i,t,2)
data_x_G2(counter2,t,3)=data_x(i,t,3)
end do
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
counter3=counter3+1
do t=1,MaxT-T_trans-50000,1
data_x_G3(counter3,t,1)=data_x(i,t,1)
data_x_G3(counter3,t,2)=data_x(i,t,2)
data_x_G3(counter3,t,3)=data_x(i,t,3)
end do
else
write(100,*) "2_区分data_x条件有误!"
end if
end do
!整合时空斑图
do i=1,counter1,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G1(i,t,1)
data_x(i,t,2)=data_x_G1(i,t,2)
data_x(i,t,3)=data_x_G1(i,t,3)
end do
end do
do i=counter1+1,counter1+counter2,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G2(i-counter1,t,1)
data_x(i,t,2)=data_x_G2(i-counter1,t,2)
data_x(i,t,3)=data_x_G2(i-counter1,t,3)
end do
end do
do i=counter1+counter2+1,M/2,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G3(i-counter1-counter2,t,1)
data_x(i,t,2)=data_x_G3(i-counter1-counter2,t,2)
data_x(i,t,3)=data_x_G3(i-counter1-counter2,t,3)
end do
end do
X_max=-1000.0
X_min=1000.0
do t=50000,MaxT-T_trans,1
call X_max_min(data_x(:,t-50000+1,1),X_max,X_min)
end do
do i=1,M,1
write(20,*) i,X_max(i),X_min(i)
end do
do i=1,M,1
do t=1,MaxT-T_trans-50000,1
if(mod(t,100)==0) then
write(30,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
end if
end do
end do
close(10)
close(20)
close(30)
close(40)
deallocate(data_x_G1)
deallocate(data_x_G2)
deallocate(data_x_G3)
deallocate(neighbour_matrix)
end program main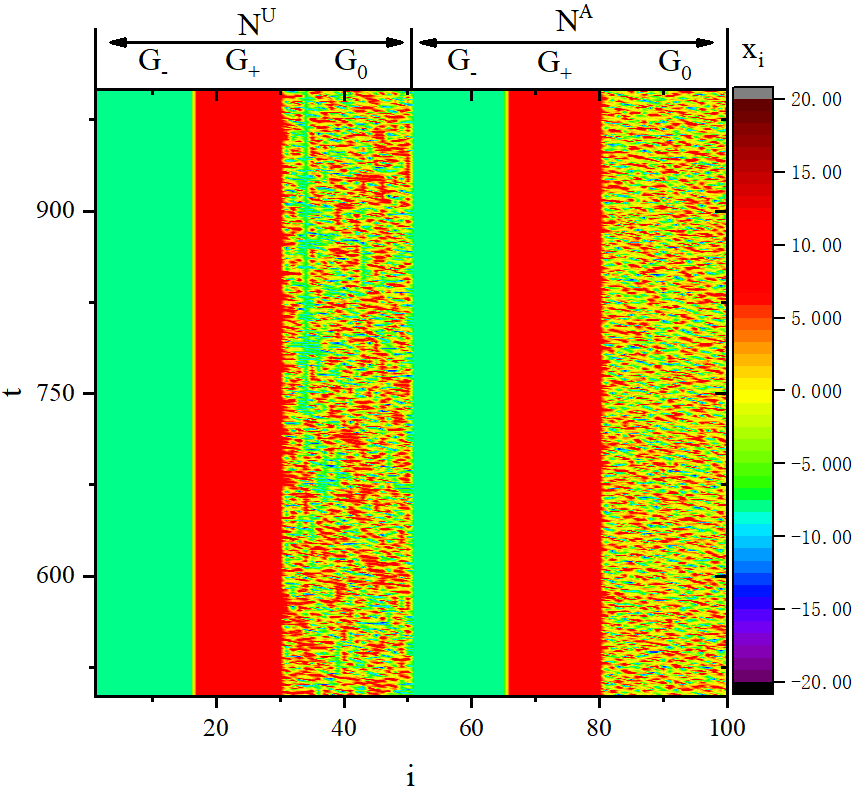

figure 4_C
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=100
real :: x(M,N),epsilon_2,E(M)=0,BB(M)=0.0
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=x1*40.0-20.0
x(i,2)=x2*50.0-25.0
x(i,3)=x3*45.0
x(i,4)=0.0
write(5,*) x(i,1),x(i,2),x(i,3),x(i,4)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB(i))
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,counter1,counter2,counter3
real :: X_max(M),X_min(M),data_x(M,MaxT-T_trans-50000,3)
real,allocatable :: data_x_G1(:,:,:),data_x_G2(:,:,:),data_x_G3(:,:,:)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="i_t_x.txt")
open(40,file="t_x_2.txt")
open(100,file="error.txt")
call neighbour()
E(1:100)=1
BB(1:30)=-7.9666
BB(31:60)=7.9666
BB(61:100)=0.0
epsilon_2=2.5
counter1=0 !B_
counter2=0 !B+
counter3=0 !B0
call x0
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
!x的时空斑图
if((t-T_trans)*h>500) then
do i=1,M,1
data_x(i,t-T_trans-50000,1) = x(i,1)
data_x(i,t-T_trans-50000,2) = x(i,2)
data_x(i,t-T_trans-50000,3) = x(i,3)
end do
end if
end if
end do
do i=1,M,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
counter1=counter1+1
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
counter2=counter2+1
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
counter3=counter3+1
else
write(100,*) "1_区分data_x条件有误!"
end if
end do
!时空斑图秩序化
allocate(data_x_G1(counter1,MaxT-T_trans-50000,3))
allocate(data_x_G2(counter2,MaxT-T_trans-50000,3))
allocate(data_x_G3(counter3,MaxT-T_trans-50000,3))
counter1=0
counter2=0
counter3=0
do i=1,M,1
!时空斑图对x分区
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G_
counter1=counter1+1
do t=1,MaxT-T_trans-50000,1
data_x_G1(counter1,t,1)=data_x(i,t,1)
data_x_G1(counter1,t,2)=data_x(i,t,2)
data_x_G1(counter1,t,3)=data_x(i,t,3)
end do
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
counter2=counter2+1
do t=1,MaxT-T_trans-50000,1
data_x_G2(counter2,t,1)=data_x(i,t,1)
data_x_G2(counter2,t,2)=data_x(i,t,2)
data_x_G2(counter2,t,3)=data_x(i,t,3)
end do
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
counter3=counter3+1
do t=1,MaxT-T_trans-50000,1
data_x_G3(counter3,t,1)=data_x(i,t,1)
data_x_G3(counter3,t,2)=data_x(i,t,2)
data_x_G3(counter3,t,3)=data_x(i,t,3)
end do
else
write(100,*) "2_区分data_x条件有误!"
end if
end do
!整合时空斑图
do i=1,counter1,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G1(i,t,1)
data_x(i,t,2)=data_x_G1(i,t,2)
data_x(i,t,3)=data_x_G1(i,t,3)
end do
end do
do i=counter1+1,counter1+counter2,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G2(i-counter1,t,1)
data_x(i,t,2)=data_x_G2(i-counter1,t,2)
data_x(i,t,3)=data_x_G2(i-counter1,t,3)
end do
end do
do i=counter1+counter2+1,M,1
do t=1,MaxT-T_trans-50000,1
data_x(i,t,1)=data_x_G3(i-counter1-counter2,t,1)
data_x(i,t,2)=data_x_G3(i-counter1-counter2,t,2)
data_x(i,t,3)=data_x_G3(i-counter1-counter2,t,3)
end do
end do
X_max=-1000.0
X_min=1000.0
do t=50000,MaxT-T_trans,1
call X_max_min(data_x(:,t-50000+1,1),X_max,X_min)
end do
do i=1,M,1
write(20,*) i,X_max(i),X_min(i)
end do
do i=1,M,1
do t=1,MaxT-T_trans-50000,1
if(mod(t,100)==0) then
write(30,*) i,t*h,data_x(i,t,1),data_x(i,t,2),data_x(i,t,3)
end if
end do
end do
close(10)
close(20)
close(30)
close(40)
deallocate(data_x_G1)
deallocate(data_x_G2)
deallocate(data_x_G3)
deallocate(neighbour_matrix)
end program main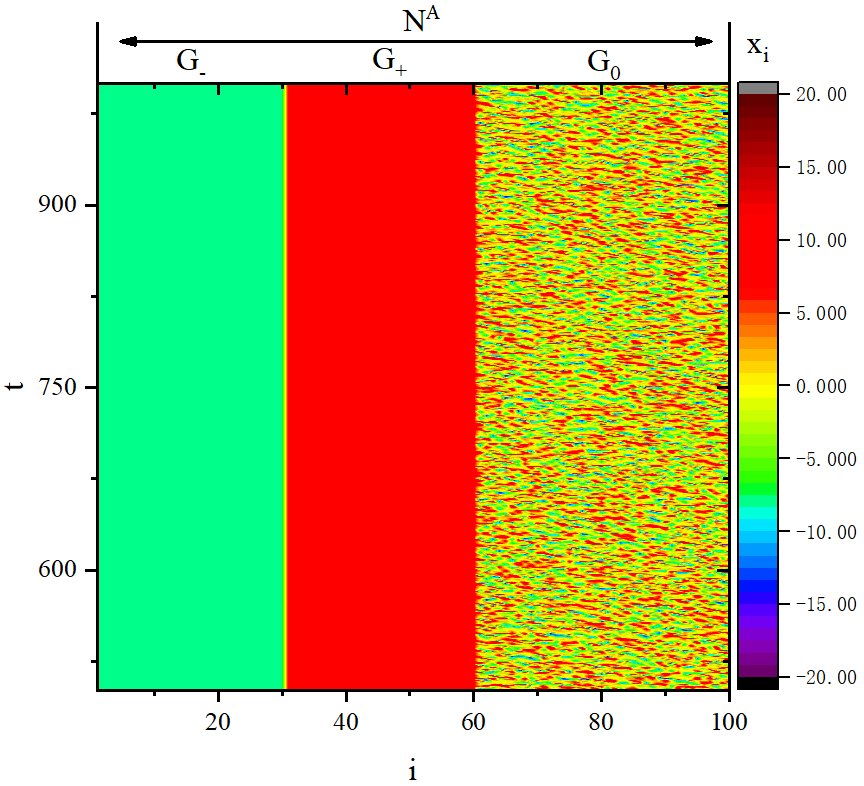

figure 4_D

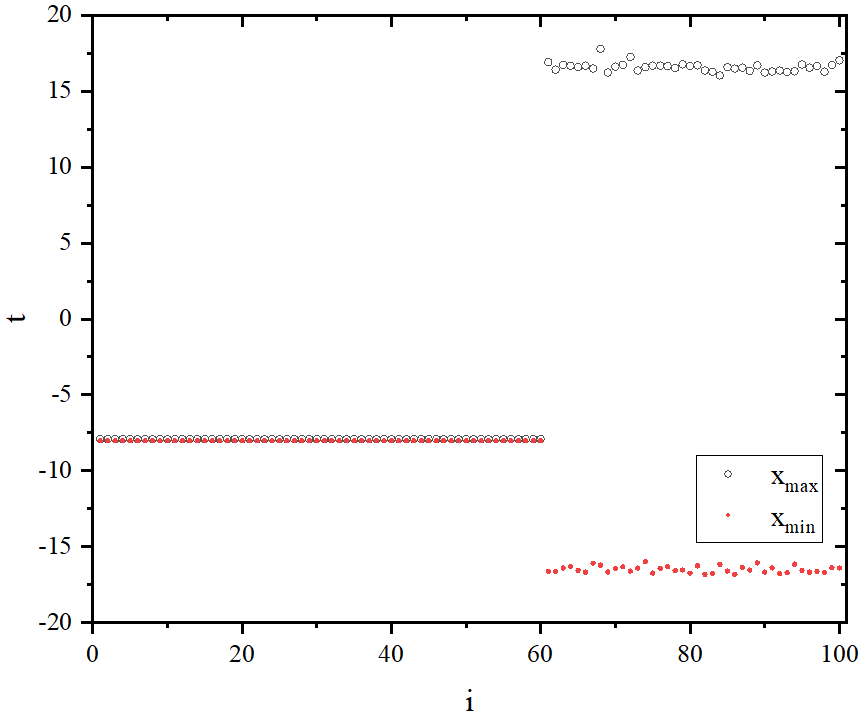
figure 5

figure 5_A
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=2
real :: x(M,N),epsilon_2,E(M)=0,BB(M)=0.0
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0(x1,x2)
implicit none
real :: x1,x2
open(5,file="x0_y0_z0.txt")
x(:,1)=1.0
x(:,2)=1.0
x(1,3)=x1
x(2,3)=x2
x(:,4)=1.0
write(5,*) x(:,1),x(:,2),x(:,3),x(:,4)
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB(i))
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,jj,a,b,state(3),index
real :: X_max(M),X_min(M),x1,x2,number
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="i_t_x.txt")
open(40,file="z_state.txt")
open(100,file="error.txt")
call random_seed()
call neighbour()
E(1:M)=1
BB(1:M)=0.0
epsilon_2=0.0
do a=1,100,1
do b=1,400,1
x1=20.0+a*0.01
x2=20.0+b*0.01
state=0
call x0(x1,x2)
X_max=-1000.0
X_min=1000.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
end if
end do
do i=1,M,1
!区分不同状态:G-;G+;G0
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
state(1)=1
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
state(2)=2
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
state(3)=3
else
write(100,*) "1_区分不同状态条件有误!"
end if
end do
!随机从数组state中取一个不为0的值
100 call random_number(number)
index = 1 + int(number * 3.0)
if(state(index)/=0) then
write(40,*) x1,x2,state(index)
write(*,*) x1,x2,state(index)
else
goto 100
end if
end do
end do
close(10)
close(20)
close(30)
close(40)
deallocate(neighbour_matrix)
end program main
figure 5_B
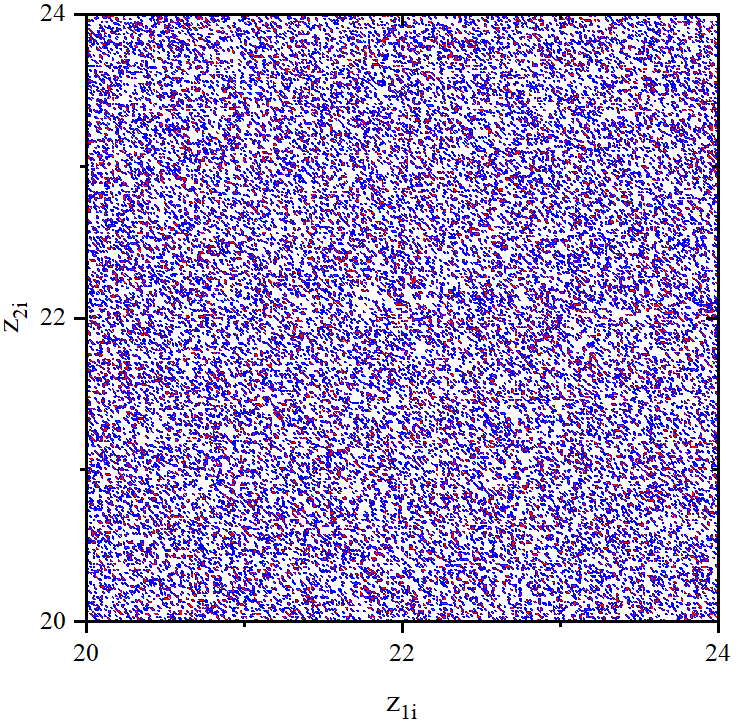
figure 5_C
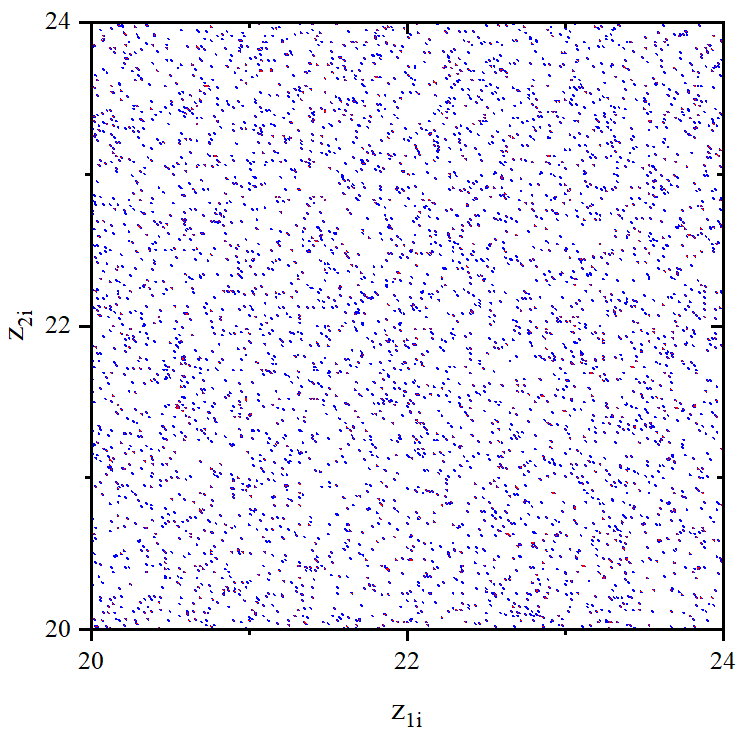
figure 5_D

figure 6
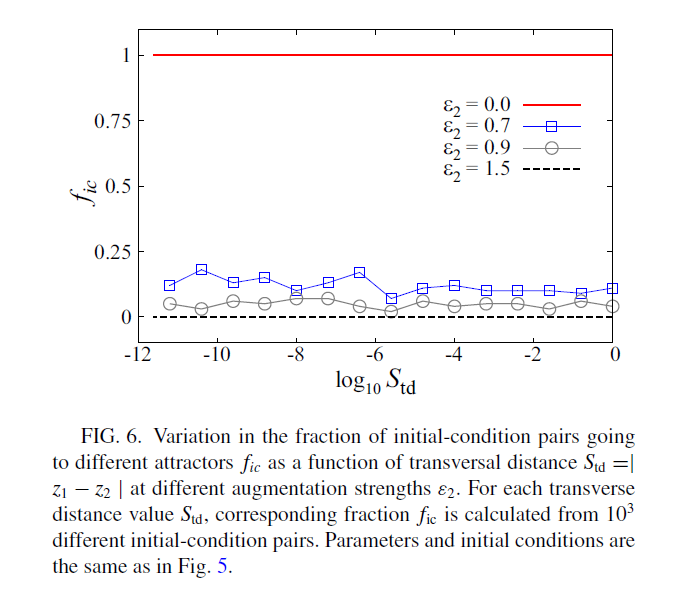
module Lorenz_control
implicit none
real,parameter :: h=0.01,PI=3.1415926
integer,parameter :: MaxT=1200000,T_trans=1100000,N=4,M=2,cycle_number=500
real(kind=8) :: x(M,N),epsilon_2,E(M)=0.0,BB(M)=0.0
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0(x1,x2)
implicit none
real(kind=8) :: x1,x2
open(5,file="x0_y0_z0.txt")
x(:,1)=1.0
x(:,2)=1.0
x(1,3)=x1
x(2,3)=x2
x(:,4)=1.0
write(5,*) x(:,1),x(:,2),x(:,3),x(:,4)
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real(kind=8) :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c,epsilon_1,K
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
epsilon_1=0.08
coupling=0.0
K=3.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))+epsilon_2*E(i)*xx(4)
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
fx(4)=-K*xx(4)-epsilon_2*E(i)*(xx(1)-BB(i))
return
end subroutine fnf
subroutine rk4(x)
implicit none
integer :: i
real(kind=8) :: x(M,N),xx(N),fx(N)
real(kind=8) :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
!Xmax与Xmin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real(kind=8) :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j,ii,jj,counter1,counter2,counter3,number1,number2,number3,counter
real(kind=8) :: X_max(M),X_min(M),x1,x2
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(30,file="i_t_x.txt")
open(40,file="Std_fic.txt")
open(100,file="error.txt")
call random_seed()
call neighbour()
E(1:M)=1
BB(1:M)=0.0
epsilon_2=0.0
do ii=12,0,-1
counter1=0
counter2=0
counter3=0
counter=0
do jj=1,cycle_number,1
call random_number(x1)
call random_number(x2)
x1=20.0+x1/real(10.0**ii)
x2=20.0+x2/real(10.0**ii)
call x0(x1,x2)
X_max=-1000.0
X_min=1000.0
number1=0
number2=0
number3=0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call X_max_min(x(:,1),X_max,X_min)
end if
end do
do i=1,M,1
!区分不同状态:G-;G+;G0
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
counter1=counter1+1
number1=number1+1
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
counter2=counter2+1
number2=number2+1
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
counter3=counter3+1
number3=number3+1
else
write(20,*) i,X_max(i),X_min(i)
write(100,*) "1_区分不同状态条件有误!"
end if
end do
if((number1==1.and.number2==1).or.(number1==1.and.number3==1).or.(number1==2.and.number3==1)) then
counter=counter+1
end if
end do
write(*,*) log10(1.0/real(10.0**ii)),counter1/real(cycle_number*M),counter2/real(cycle_number*M),&
counter3/real(cycle_number*M),counter/real(cycle_number)
write(40,*) log10(1.0/real(10.0**ii)),counter1/real(cycle_number*M),counter2/real(cycle_number*M),&
counter3/real(cycle_number*M),counter/real(cycle_number)
end do
close(10)
close(20)
close(30)
close(40)
deallocate(neighbour_matrix)
end program main
figure 7
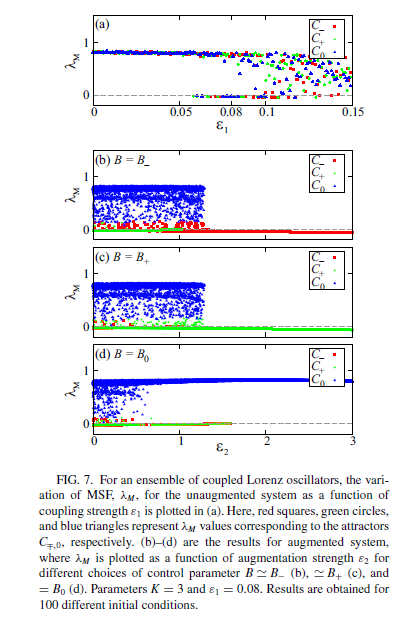
主稳定方程(Master Stability Function, MSF)
- 主稳定性方程是一种用于分析和预测动态网络同步性质的数学工具。它通过将网络中节点之间的耦合函数和节点的动力学方程组合起来,得到一个描述网络同步行为的方程。主稳定方程可以用于判断网络是否会达到同步状态,以及同步状态的稳定性。以下是一些步骤来确定网络中的同步状态:
- ①确定耦合函数:首先,你需要确定网络中节点之间的耦合方式。耦合函数描述了节点之间的相互作用方式,可以是线性或非线性的,并且可能依赖于节点之间的距离或拓扑结构。
- ②构建动力学方程:对于每个节点,你需要定义其动力学方程。这些方程描述了节点的状态随时间的演化规律,可以是连续时间或离散时间的。节点的动力学方程可以基于其内部特性和与其他节点的耦合作用来定义。
- ③确定线性稳定性:将耦合函数和节点的动力学方程组合起来,得到网络的主稳定方程。主稳定方程通常是一组差分方程或微分方程,描述了节点状态之间的关系以及节点同步的演化。线性稳定性分析可以通过线性化主稳定方程来进行,从而判断同步状态的稳定性。
- ④计算特征值:解决主稳定方程,计算特征值和特征向量。特征值表示系统的本征频率,特征向量表示节点状态的演化模式。特征值的实部和虚部可以用来判断同步的稳定性和振荡频率。
- ⑤分析稳定性:通过分析特征值的位置和性质,可以判断网络是否会达到同步状态,以及同步状态的稳定性。具有负实部的特征值表示同步稳定,而具有正实部的特征值表示同步不稳定。
figure 7_A
- 使用三种动力学下的最大李指数
module Lorenz_control
implicit none
real,parameter :: h=0.01
integer,parameter :: MaxT=10700000,T_trans=10500000,N=3,M=100
real :: x(M,N),x1(M,N),epsilon_1
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=int(x1*40.0-20.0)
x(i,2)=int(x2*50.0-25.0)
x(i,3)=int(x3*45.0)
write(5,*) x(i,1),x(i,2),x(i,3)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
return
end subroutine fnf
subroutine Msf(xx,xx1,fx1,i)
implicit none
real :: xx(N),xx1(N),fx1(N),coupling !xx:x,y,z;xx1:dx,dy,dz
integer :: t,i,j
real :: a,b,c
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x1(j,3)-x1(i,3))
end do
fx1(1)=a*(xx1(2)-xx1(1))
fx1(2)=(c-xx(3))*xx1(1)-xx1(2)-xx(1)*xx1(3)
fx1(3)=xx(2)*xx1(1)+xx(1)*xx1(2)-b*xx1(3)+(epsilon_1/real(M-1))*coupling
return
end subroutine Msf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
subroutine rk4_Msf(x,x1)
implicit none
integer :: i
real :: x(M,N),x1(M,N),xx(N),xx1(N),fx(N),fx1(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N),Mx1(N),Mx2(N),Mx3(N),Mx4(N)
do i=1,M,1
xx=x(i,:)
xx1=x1(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call Msf(xx,xx1,fx1,i)
Mx1=h*fx1
xx1=x1(i,:)+0.5*Mx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call Msf(xx,xx1,fx1,i)
Mx2=h*fx1
xx1=x1(i,:)+0.5*Mx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call Msf(xx,xx1,fx1,i)
Mx3=h*fx1
xx1=x1(i,:)+0.5*Mx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
call Msf(xx,xx1,fx1,i)
Mx4=h*fx1
x1(i,:)=x1(i,:)+(Mx1+2.0*Mx2+2.0*Mx3+Mx4)/6.0
end do
return
end subroutine rk4_Msf
!Umax与Umin
subroutine U_max_min(xxx,U_max,U_min)
implicit none
real :: U_max(M),U_min(M),xxx(M)
integer :: i
do i=1,M,1
if(U_max(i)<xxx(i)) then
U_max(i)=xxx(i)
end if
if(U_min(i)>xxx(i)) then
U_min(i)=xxx(i)
end if
end do
return
end subroutine U_max_min
!Umax与Umin
subroutine U_max_min1(xxx,U_max,U_min)
implicit none
real :: U_max(M),U_min(M),xxx(M)
integer :: i
do i=1,M,1
if(U_max(i)<xxx(i)) then
U_max(i)=xxx(i)
end if
if(U_min(i)>xxx(i)) then
U_min(i)=xxx(i)
end if
end do
return
end subroutine U_max_min1
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j
real :: U_max(M),U_min(M),U_max1(M),U_min1(M),data(M,MaxT-T_trans,3),d0=1.0e-6,lay(M)
real :: G1(MaxT-T_trans,4),G2(MaxT-T_trans,4),G3(MaxT-T_trans,4)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(21,file="xmax1_xmin1.txt")
open(30,file="epsilon1_lay.txt")
open(40,file="G1.txt")
open(50,file="G2.txt")
open(60,file="G3.txt")
call neighbour()
call x0
U_max=-1000.0
U_min=1000.0
U_max1=-1000.0
U_min1=1000.0
epsilon_1=0.05
x1(:,1)=0.0+d0
x1(:,2)=0.0
x1(:,3)=0.0
G1=0.0
G2=0.0
G3=0.0
do t=1,MaxT-T_trans,1
read(40,*) G1(t,1),G1(t,2),G1(t,3),G1(t,4)
read(50,*) G2(t,1),G2(t,2),G2(t,3),G2(t,4)
read(60,*) G3(t,1),G3(t,2),G3(t,3),G3(t,4)
end do
lay=0.0
do t=1,MaxT-T_trans,1
x(:,1)=G1(t,2)
x(:,2)=G1(t,3)
x(:,3)=G1(t,4)
call rk4_Msf(x,x1)
do i=1,M,1
lay(i)=lay(i)+log((sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2))/d0)
x1(i,1)=d0*x1(i,1)/sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2)
x1(i,2)=d0*x1(i,2)/sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2)
x1(i,3)=d0*x1(i,3)/sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2)
end do
call U_max_min(x(:,1),U_max,U_min)
call U_max_min(x1(:,1),U_max1,U_min1)
end do
do i=1,M,1
write(20,*) i,U_max(i),U_min(i)
write(21,*) i,U_max1(i),U_min1(i)
write(30,*) epsilon_1,i,lay(i)/((MaxT-T_trans)*h)
end do
close(10)
close(20)
close(30)
deallocate(neighbour_matrix)
end program main- 随机初值
module Lorenz_control
implicit none
real,parameter :: h=0.01
integer,parameter :: MaxT=10700000,T_trans=10500000,T_trans2=10600000,N=3,M=100
real :: x(M,N),x1(M,N),epsilon_1
integer,allocatable :: neighbour_matrix(:,:)
contains
subroutine x0()
implicit none
integer :: i
real :: x1,x2,x3
call random_seed()
open(5,file="x0_y0_z0.txt")
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i,1)=int(x1*40.0-20.0)
x(i,2)=int(x2*50.0-25.0)
x(i,3)=int(x3*45.0)
write(5,*) x(i,1),x(i,2),x(i,3)
end do
close(5)
end subroutine x0
subroutine fnf(xx,fx,i)
implicit none
real :: xx(N),fx(N),coupling
integer :: t,i,j
real :: a,b,c
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x(j,3)-x(i,3))
end do
fx(1)=a*(xx(2)-xx(1))
fx(2)=c*xx(1)-xx(2)-xx(1)*xx(3)
fx(3)=xx(1)*xx(2)-b*xx(3)+(epsilon_1/real(M-1))*coupling
return
end subroutine fnf
subroutine Msf(xx,xx1,fx1,i)
implicit none
real :: xx(N),xx1(N),fx1(N),coupling !xx:x,y,z;xx1:dx,dy,dz
integer :: t,i,j
real :: a,b,c
a=10.0 !sigma
b=8.0/3.0 !beta
c=24.8 !r
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(x1(j,3)-x1(i,3))
end do
fx1(1)=a*(xx1(2)-xx1(1))
fx1(2)=(c-xx(3))*xx1(1)-xx1(2)-xx(1)*xx1(3)
fx1(3)=xx(2)*xx1(1)+xx(1)*xx1(2)-b*xx1(3)+(epsilon_1/real(M-1))*coupling
return
end subroutine Msf
subroutine rk4(x)
implicit none
integer :: i
real :: x(M,N),xx(N),fx(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N)
do i=1,M,1
xx=x(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
end do
return
end subroutine rk4
subroutine rk4_Msf(x,x1)
implicit none
integer :: i
real :: x(M,N),x1(M,N),xx(N),xx1(N),fx(N),fx1(N)
real :: kx1(N),kx2(N),kx3(N),kx4(N),Mx1(N),Mx2(N),Mx3(N),Mx4(N)
do i=1,M,1
xx=x(i,:)
xx1=x1(i,:)
call fnf(xx,fx,i)
kx1=h*fx
xx=x(i,:)+0.5*kx1
call Msf(xx,xx1,fx1,i)
Mx1=h*fx1
xx1=x1(i,:)+0.5*Mx1
call fnf(xx,fx,i)
kx2=h*fx
xx=x(i,:)+0.5*kx2
call Msf(xx,xx1,fx1,i)
Mx2=h*fx1
xx1=x1(i,:)+0.5*Mx2
call fnf(xx,fx,i)
kx3=h*fx
xx=x(i,:)+kx3
call Msf(xx,xx1,fx1,i)
Mx3=h*fx1
xx1=x1(i,:)+0.5*Mx3
call fnf(xx,fx,i)
kx4=h*fx
x(i,:)=x(i,:)+(kx1+2.0*kx2+2.0*kx3+kx4)/6.0
call Msf(xx,xx1,fx1,i)
Mx4=h*fx1
x1(i,:)=x1(i,:)+(Mx1+2.0*Mx2+2.0*Mx3+Mx4)/6.0
end do
return
end subroutine rk4_Msf
!Umax与Umin
subroutine U_max_min(xxx,U_max,U_min)
implicit none
real :: U_max(M),U_min(M),xxx(M)
integer :: i
do i=1,M,1
if(U_max(i)<xxx(i)) then
U_max(i)=xxx(i)
end if
if(U_min(i)>xxx(i)) then
U_min(i)=xxx(i)
end if
end do
return
end subroutine U_max_min
!Umax与Umin
subroutine U_max_min1(xxx,U_max,U_min)
implicit none
real :: U_max(M),U_min(M),xxx(M)
integer :: i
do i=1,M,1
if(U_max(i)<xxx(i)) then
U_max(i)=xxx(i)
end if
if(U_min(i)>xxx(i)) then
U_min(i)=xxx(i)
end if
end do
return
end subroutine U_max_min1
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(10,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(10,*)
end do
return
end subroutine neighbour
end module Lorenz_control
program main
use Lorenz_control
implicit none
integer :: t,i,j
real :: U_max(M),U_min(M),U_max1(M),U_min1(M),data(M,MaxT-T_trans,3),d0=1.0e-6,lay(M)
open(10,file="neighbour_matrix.txt")
open(20,file="xmax_xmin.txt")
open(21,file="xmax1_xmin1.txt")
open(30,file="epsilon1_lay.txt")
call neighbour()
do j=1,151,1
epsilon_1=j*0.001-0.001
call x0
U_max=-1000.0
U_min=1000.0
U_max1=-1000.0
U_min1=1000.0
x1(:,1)=0.0+d0
x1(:,2)=0.0
x1(:,3)=0.0
lay=0.0
do t=1,MaxT,1
call rk4(x)
if(t>T_trans) then
call rk4_Msf(x,x1)
do i=1,M,1
lay(i)=lay(i)+log((sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2))/d0)
x1(i,1)=d0*x1(i,1)/sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2)
x1(i,2)=d0*x1(i,2)/sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2)
x1(i,3)=d0*x1(i,3)/sqrt(x1(i,1)**2+x1(i,2)**2+x1(i,3)**2)
end do
call U_max_min(x(:,1),U_max,U_min)
call U_max_min(x1(:,1),U_max1,U_min1)
end if
end do
do i=1,M,1
write(20,*) i,U_max(i),U_min(i)
write(21,*) i,U_max1(i),U_min1(i)
write(30,*) epsilon_1,i,lay(i)/((MaxT-T_trans)*h)
end do
end do
close(10)
close(20)
close(30)
deallocate(neighbour_matrix)
end program main修改版1
module Lorenz_Control implicit none real,parameter :: h=0.01 integer,parameter :: M=100 real*8::dx(M),dy(M),dz(M),x(M),y(M),z(M) real*8::dx1(M),dy1(M),dz1(M) real*8::epsilon_1 real*8::d0=1.0e-6 integer,allocatable :: neighbour_matrix(:,:) contains !========================= subroutine msf(x,y,z,dx,dy,dz) implicit none integer :: i real*8::x(M),y(M),z(M) real*8::x1(M),y1(M),z1(M) real*8::fx(M),fy(M),fz(M) real*8::kx1(M),kx2(M),kx3(M),kx4(M) real*8::ky1(M),ky2(M),ky3(M),ky4(M) real*8::kz1(M),kz2(M),kz3(M),kz4(M) real*8::dx(M),dy(M),dz(M) real*8::dx1(M),dy1(M),dz1(M) real*8::fdx(M),fdy(M),fdz(M) real*8::fx1(M),fx2(M),fx3(M),fx4(M) real*8::fy1(M),fy2(M),fy3(M),fy4(M) real*8::fz1(M),fz2(M),fz3(M),fz4(M) !========================= x1=x y1=y z1=z do i=1,M,1 call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx1(i)=h*fx(i) ky1(i)=h*fy(i) kz1(i)=h*fz(i) dx1(i)=dx(i) dy1(i)=dy(i) dz1(i)=dz(i) call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i) fx1(i)=h*fdx(i) fy1(i)=h*fdy(i) fz1(i)=h*fdz(i) !========================= x1(i)=x(i)+0.5*kx1(i) y1(i)=y(i)+0.5*ky1(i) z1(i)=z(i)+0.5*kz1(i) call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx2(i)=h*fx(i) ky2(i)=h*fy(i) kz2(i)=h*fz(i) dx1(i)=dx(i)+0.5*fx1(i) dy1(i)=dy(i)+0.5*fy1(i) dz1(i)=dz(i)+0.5*fz1(i) call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i) fx2(i)=h*fdx(i) fy2(i)=h*fdy(i) fz2(i)=h*fdz(i) !========================= x1(i)=x(i)+0.5*kx2(i) y1(i)=y(i)+0.5*ky2(i) z1(i)=z(i)+0.5*kz2(i) call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx3(i)=h*fx(i) ky3(i)=h*fy(i) kz3(i)=h*fz(i) dx1(i)=dx(i)+0.5*fx2(i) dy1(i)=dy(i)+0.5*fy2(i) dz1(i)=dz(i)+0.5*fz2(i) call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i) fx3(i)=h*fdx(i) fy3(i)=h*fdy(i) fz3(i)=h*fdz(i) !========================= x1(i)=x(i)+kx3(i) y1(i)=y(i)+ky3(i) z1(i)=z(i)+kz3(i) call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx4(i)=h*fx(i) ky4(i)=h*fy(i) kz4(i)=h*fz(i) dx1(i)=dx(i)+fx3(i) dy1(i)=dy(i)+fy3(i) dz1(i)=dz(i)+fz3(i) call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i) fx4(i)=h*fdx(i) fy4(i)=h*fdy(i) fz4(i)=h*fdz(i) !========================= x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0 y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0 z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0 dx(i)=dx(i)+(fx1(i)+2.0*fx2(i)+2.0*fx3(i)+fx4(i))/6.0 dy(i)=dy(i)+(fy1(i)+2.0*fy2(i)+2.0*fy3(i)+fy4(i))/6.0 dz(i)=dz(i)+(fz1(i)+2.0*fz2(i)+2.0*fz3(i)+fz4(i))/6.0 end do return end subroutine !========================= subroutine fun1(x,y,z,dx,dy,dz1,fdx,fdy,fdz,i) implicit none real*8::dx,dy,dz1,coupling real*8::x,y,z real*8::fdx,fdy,fdz real*8::a=10.0,b=8.0/3.0,r=24.8 integer :: i,j coupling=0.0 do j=1,M,1 coupling=coupling+neighbour_matrix(i,j)*(dz(j)-dz(i)) end do fdx=a*(dy-dx) fdy=(r-z)*dx-dy-x*dz1 fdz=y*dx+x*dy-b*dz1-(epsilon_1/real(M-1))*coupling endsubroutine !========================= subroutine fun(x,y,z1,fx,fy,fz,i) real*8::x,y,z1,fx,fy,fz,coupling real*8::a,b,r integer :: i,j a=10.0 b=8.0/3.0 r=24.8 coupling=0.0 do j=1,M,1 coupling=coupling+neighbour_matrix(i,j)*(z(j)-z(i)) end do fx=a*(y-x) fy=r*x-y-x*z1 fz=x*y-b*z1+(epsilon_1/real(M-1))*coupling end subroutine !========================= !========================= subroutine lorenz(x,y,z) implicit none integer :: i real*8::x(M),y(M),z(M) real*8::x1(M),y1(M),z1(M) real*8::kx1(M),kx2(M),kx3(M),kx4(M) real*8::ky1(M),ky2(M),ky3(M),ky4(M) real*8::kz1(M),kz2(M),kz3(M),kz4(M) real*8::fx(M),fy(M),fz(M) x1=x y1=y z1=z do i=1,M,1 call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx1(i)=h*fx(i) ky1(i)=h*fy(i) kz1(i)=h*fz(i) x1(i)=x(i)+0.5*kx1(i) y1(i)=y(i)+0.5*ky1(i) z1(i)=z(i)+0.5*kz1(i) call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx2(i)=h*fx(i) ky2(i)=h*fy(i) kz2(i)=h*fz(i) x1(i)=x(i)+0.5*kx2(i) y1(i)=y(i)+0.5*ky2(i) z1(i)=z(i)+0.5*kz2(i) call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx3(i)=h*fx(i) ky3(i)=h*fy(i) kz3(i)=h*fz(i) x1(i)=x(i)+kx3(i) y1(i)=y(i)+ky3(i) z1(i)=z(i)+kz3(i) call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i) kx4(i)=h*fx(i) ky4(i)=h*fy(i) kz4(i)=h*fz(i) x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0d0 y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0d0 z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0d0 end do return end subroutine !建立网络结构:全局耦合 subroutine neighbour() implicit none integer :: i,j,number allocate(neighbour_matrix(M,M)) !初始化网络矩阵 neighbour_matrix=0 do i=1,M-1,1 do j=i+1,M,1 neighbour_matrix(i,j)=1 neighbour_matrix(j,i)=1 end do end do !输出矩阵 do i=1,M,1 do j=1,M,1 write(20,"(I2)",advance='no') neighbour_matrix(i,j) end do write(20,*) end do return end subroutine neighbour
end module Lorenz_Control
program main
use Lorenz_Control
implicit none
integer4::i,ii,j
real8::x1,x2,x3
real8::lay(M)
open(10,file=”k_lay.txt”)
open(20,file=”neighbour_matrix.txt”)
call neighbour()
DO j=1,101,1
epsilon_1=j0.0015-0.0015
!=========================
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i)=int(x140.0-20.0)
y(i)=int(x250.0-25.0)
z(i)=int(x345.0)
end do
DO i=1,100000
call lorenz(x,y,z)
ENDDO
dx=d0
dy=0.0
dz=0.0
!=========================
lay=0
DO i=1,2000000
call msf(x,y,z,dx,dy,dz)
dx1=dx
dy1=dy
dz1=dz
do ii=1,M,1
lay(ii)=lay(ii)+log((sqrt(dx(ii)2+dy(ii)2+dz(ii)2))/d0)
dx(ii)=d0*dx(ii)/sqrt(dx1(ii)2+dy1(ii)2+dz1(ii)2)
dy(ii)=d0dy(ii)/sqrt(dx1(ii)*2+dy1(ii)2+dz1(ii)2)
dz(ii)=d0dz(ii)/sqrt(dx1(ii)*2+dy1(ii)2+dz1(ii)2)
end do
ENDDO
do i=1,1,1
write(10,) epsilon_1,lay(i)/2000000.0/0.01
write(,) epsilon_1,lay(i)/2000000.0/0.01
end do
ENDDO
close(10)
deallocate(neighbour_matrix)
end program main
* 结果版
```fortran
module Lorenz_Control
implicit none
real,parameter :: h=0.01
integer,parameter :: M=100
real*8::dx(M),dy(M),dz(M),x(M),y(M),z(M)
real*8::dx1(M),dy1(M),dz1(M)
real*8::epsilon_1
real*8::d0=1.0e-6
integer,allocatable :: neighbour_matrix(:,:)
contains
!=========================
subroutine msf(x,y,z,dx,dy,dz)
implicit none
integer :: i
real*8::x(M),y(M),z(M)
real*8::x1(M),y1(M),z1(M)
real*8::fx(M),fy(M),fz(M)
real*8::kx1(M),kx2(M),kx3(M),kx4(M)
real*8::ky1(M),ky2(M),ky3(M),ky4(M)
real*8::kz1(M),kz2(M),kz3(M),kz4(M)
real*8::dx(M),dy(M),dz(M)
real*8::dx1(M),dy1(M),dz1(M)
real*8::fdx(M),fdy(M),fdz(M)
real*8::fx1(M),fx2(M),fx3(M),fx4(M)
real*8::fy1(M),fy2(M),fy3(M),fy4(M)
real*8::fz1(M),fz2(M),fz3(M),fz4(M)
!=========================
x1=x
y1=y
z1=z
do i=1,M,1
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx1(i)=h*fx(i)
ky1(i)=h*fy(i)
kz1(i)=h*fz(i)
dx1(i)=dx(i)
dy1(i)=dy(i)
dz1(i)=dz(i)
call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i)
fx1(i)=h*fdx(i)
fy1(i)=h*fdy(i)
fz1(i)=h*fdz(i)
!=========================
x1(i)=x(i)+0.5*kx1(i)
y1(i)=y(i)+0.5*ky1(i)
z1(i)=z(i)+0.5*kz1(i)
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx2(i)=h*fx(i)
ky2(i)=h*fy(i)
kz2(i)=h*fz(i)
dx1(i)=dx(i)+0.5*fx1(i)
dy1(i)=dy(i)+0.5*fy1(i)
dz1(i)=dz(i)+0.5*fz1(i)
call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i)
fx2(i)=h*fdx(i)
fy2(i)=h*fdy(i)
fz2(i)=h*fdz(i)
!=========================
x1(i)=x(i)+0.5*kx2(i)
y1(i)=y(i)+0.5*ky2(i)
z1(i)=z(i)+0.5*kz2(i)
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx3(i)=h*fx(i)
ky3(i)=h*fy(i)
kz3(i)=h*fz(i)
dx1(i)=dx(i)+0.5*fx2(i)
dy1(i)=dy(i)+0.5*fy2(i)
dz1(i)=dz(i)+0.5*fz2(i)
call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i)
fx3(i)=h*fdx(i)
fy3(i)=h*fdy(i)
fz3(i)=h*fdz(i)
!=========================
x1(i)=x(i)+kx3(i)
y1(i)=y(i)+ky3(i)
z1(i)=z(i)+kz3(i)
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx4(i)=h*fx(i)
ky4(i)=h*fy(i)
kz4(i)=h*fz(i)
dx1(i)=dx(i)+fx3(i)
dy1(i)=dy(i)+fy3(i)
dz1(i)=dz(i)+fz3(i)
call fun1(x1(i),y1(i),z1(i),dx1(i),dy1(i),dz1(i),fdx(i),fdy(i),fdz(i),i)
fx4(i)=h*fdx(i)
fy4(i)=h*fdy(i)
fz4(i)=h*fdz(i)
!=========================
x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0
y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0
z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0
dx(i)=dx(i)+(fx1(i)+2.0*fx2(i)+2.0*fx3(i)+fx4(i))/6.0
dy(i)=dy(i)+(fy1(i)+2.0*fy2(i)+2.0*fy3(i)+fy4(i))/6.0
dz(i)=dz(i)+(fz1(i)+2.0*fz2(i)+2.0*fz3(i)+fz4(i))/6.0
end do
return
end subroutine
!=========================
subroutine fun1(x,y,z,dx,dy,dz,fdx,fdy,fdz,i)
implicit none
real*8::dx,dy,dz,coupling
real*8::x,y,z
real*8::fdx,fdy,fdz
real*8::a=10.0,b=8.0/3.0,r=24.8
integer :: i,j
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)
end do
fdx=a*(dy-dx)
fdy=(r-z)*dx-dy-x*dz
fdz=y*dx+x*dy-b*dz-(epsilon_1/real(M-1))*coupling*dz
endsubroutine
!=========================
subroutine fun(x,y,z1,fx,fy,fz,i)
real*8::x,y,z1,fx,fy,fz,coupling
real*8::a,b,r
integer :: i,j
a=10.0
b=8.0/3.0
r=24.8
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(z(j)-z(i))
end do
fx=a*(y-x)
fy=r*x-y-x*z1
fz=x*y-b*z1+(epsilon_1/real(M-1))*coupling
end subroutine
!=========================
!=========================
subroutine lorenz(x,y,z)
implicit none
integer :: i
real*8::x(M),y(M),z(M)
real*8::x1(M),y1(M),z1(M)
real*8::kx1(M),kx2(M),kx3(M),kx4(M)
real*8::ky1(M),ky2(M),ky3(M),ky4(M)
real*8::kz1(M),kz2(M),kz3(M),kz4(M)
real*8::fx(M),fy(M),fz(M)
x1=x
y1=y
z1=z
do i=1,M,1
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx1(i)=h*fx(i)
ky1(i)=h*fy(i)
kz1(i)=h*fz(i)
x1(i)=x(i)+0.5*kx1(i)
y1(i)=y(i)+0.5*ky1(i)
z1(i)=z(i)+0.5*kz1(i)
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx2(i)=h*fx(i)
ky2(i)=h*fy(i)
kz2(i)=h*fz(i)
x1(i)=x(i)+0.5*kx2(i)
y1(i)=y(i)+0.5*ky2(i)
z1(i)=z(i)+0.5*kz2(i)
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx3(i)=h*fx(i)
ky3(i)=h*fy(i)
kz3(i)=h*fz(i)
x1(i)=x(i)+kx3(i)
y1(i)=y(i)+ky3(i)
z1(i)=z(i)+kz3(i)
call fun(x1(i),y1(i),z1(i),fx(i),fy(i),fz(i),i)
kx4(i)=h*fx(i)
ky4(i)=h*fy(i)
kz4(i)=h*fz(i)
x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0d0
y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0d0
z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0d0
end do
return
end subroutine
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(20,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(20,*)
end do
return
end subroutine neighbour
!Umax与Umin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real*8 :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
end module Lorenz_Control
program main
use Lorenz_Control
implicit none
integer*4::i,ii,j,t
real*8::x1,x2,x3
real*8::lay(M),X_max(M),X_min(M)
open(10,file="k_lay_G-.txt")
open(11,file="k_lay_G+.txt")
open(12,file="k_lay_G0.txt")
open(13,file="k_lay.txt")
open(20,file="neighbour_matrix.txt")
call neighbour()
DO j=1,101,1
epsilon_1=j*0.0015-0.0015
!=========================
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i)=int(x1*40.0-20.0)
y(i)=int(x2*50.0-25.0)
z(i)=int(x3*45.0)
end do
X_max=-1000.0
X_min=1000.0
DO t=1,100000,1
call lorenz(x,y,z)
if(t>90000) then
call X_max_min(x(:),X_max,X_min)
end if
ENDDO
dx=d0
dy=0.0
dz=0.0
!=========================
lay=0
DO i=1,2000000
call msf(x,y,z,dx,dy,dz)
dx1=dx
dy1=dy
dz1=dz
do ii=1,M,1
lay(ii)=lay(ii)+log((sqrt(dx(ii)**2+dy(ii)**2+dz(ii)**2))/d0)
dx(ii)=d0*dx(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2)
dy(ii)=d0*dy(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2)
dz(ii)=d0*dz(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2)
end do
ENDDO
do i=1,M,1
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G-
write(10,*) i,epsilon_1,lay(i)/2000000.0/0.01
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
write(11,*) i,epsilon_1,lay(i)/2000000.0/0.01
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
write(12,*) i,epsilon_1,lay(i)/2000000.0/0.01
end if
write(13,*) epsilon_1,lay(10)/2000000.0/0.01
write(*,*) epsilon_1,lay(i)/2000000.0/0.01
end do
ENDDO
close(10)
deallocate(neighbour_matrix)
end program main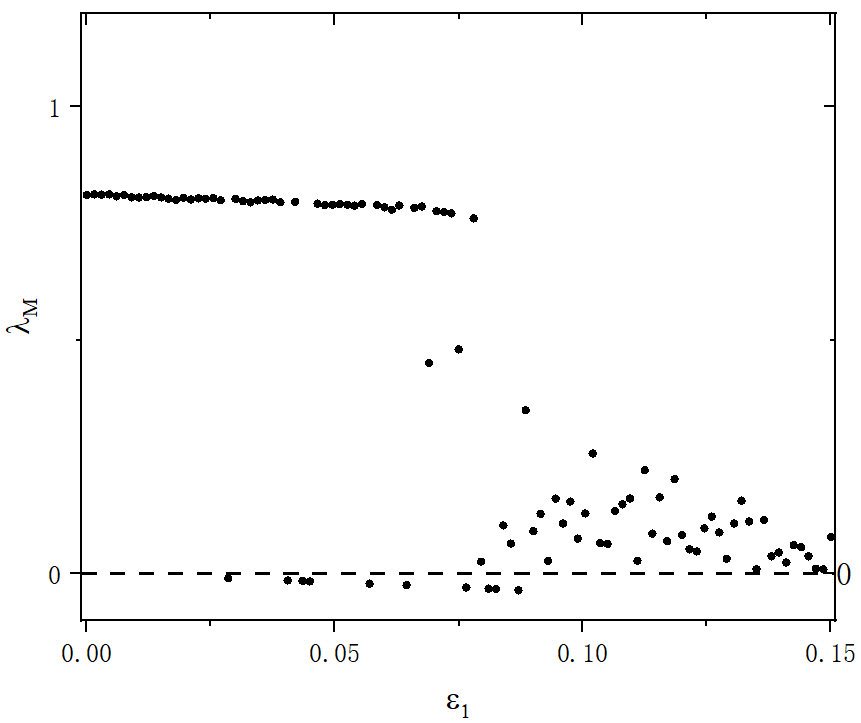
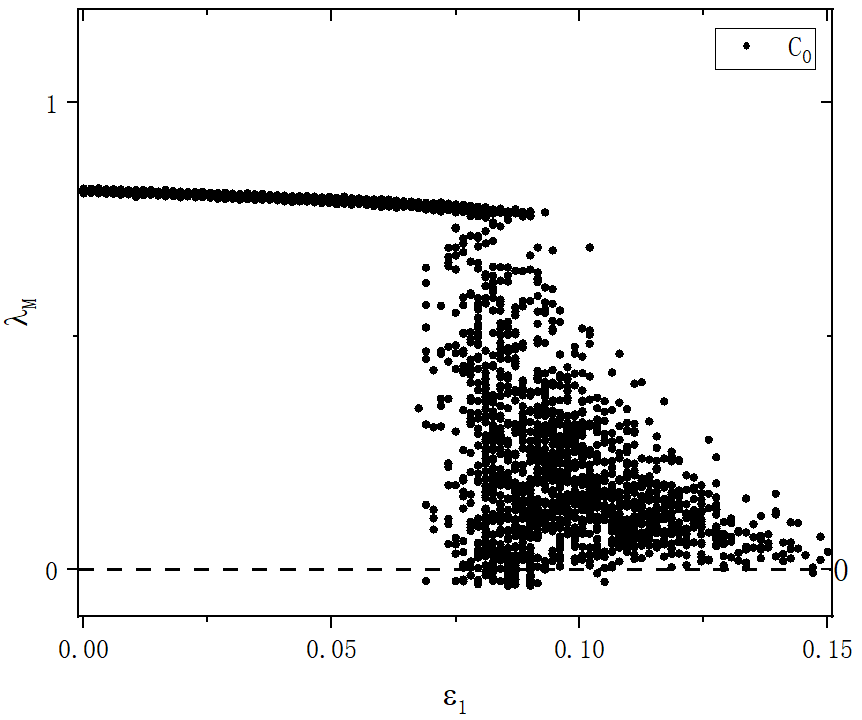

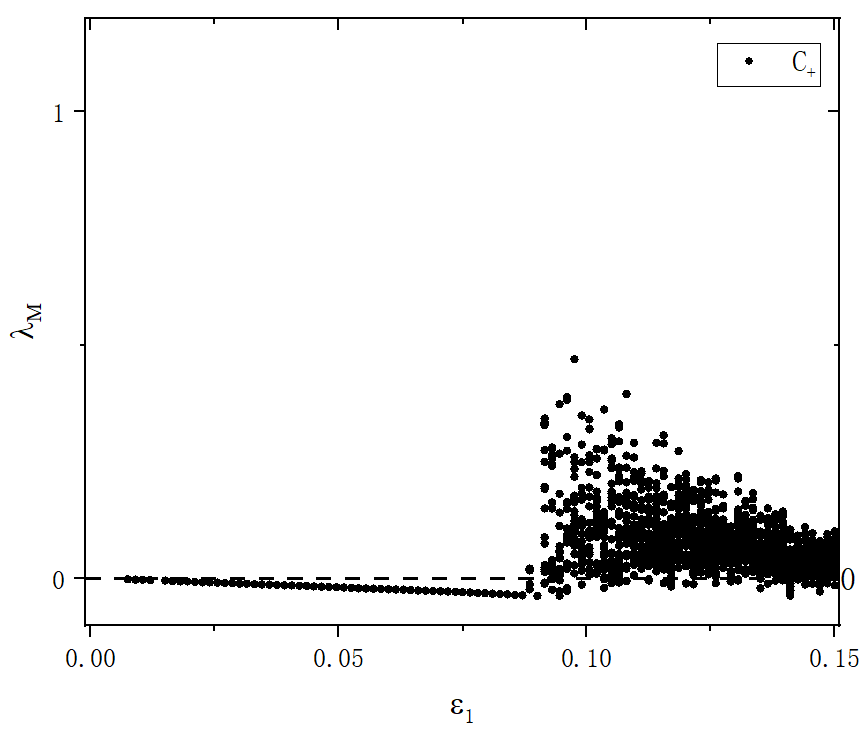
figure 7_B
module Lorenz_Control
implicit none
real,parameter :: h=0.01
integer,parameter :: M=100
real*8::dx(M),dy(M),dz(M),dw(M),x(M),y(M),z(M),w(M)
real*8::dx1(M),dy1(M),dz1(M),dw1(M)
real*8::epsilon_1=0.08,epsilon_2
real*8::d0=1.0e-6,BB=-7.9666,E(M),K=3.0
integer,allocatable :: neighbour_matrix(:,:)
contains
!=========================
subroutine msf(x,y,z,w,dx,dy,dz,dw)
implicit none
integer :: i
real*8::x(M),y(M),z(M),w(M)
real*8::x1(M),y1(M),z1(M),w1(M)
real*8::fx(M),fy(M),fz(M),fw(M)
real*8::kx1(M),kx2(M),kx3(M),kx4(M)
real*8::ky1(M),ky2(M),ky3(M),ky4(M)
real*8::kz1(M),kz2(M),kz3(M),kz4(M)
real*8::kw1(M),kw2(M),kw3(M),kw4(M)
real*8::dx(M),dy(M),dz(M),dw(M)
real*8::dx1(M),dy1(M),dz1(M),dw1(M)
real*8::fdx(M),fdy(M),fdz(M),fdw(M)
real*8::fx1(M),fx2(M),fx3(M),fx4(M)
real*8::fy1(M),fy2(M),fy3(M),fy4(M)
real*8::fz1(M),fz2(M),fz3(M),fz4(M)
real*8::fw1(M),fw2(M),fw3(M),fw4(M)
!=========================
x1=x
y1=y
z1=z
w1=w
do i=1,M,1
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx1(i)=h*fx(i)
ky1(i)=h*fy(i)
kz1(i)=h*fz(i)
kw1(i)=h*fw(i)
dx1(i)=dx(i)
dy1(i)=dy(i)
dz1(i)=dz(i)
dw1(i)=dw(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx1(i)=h*fdx(i)
fy1(i)=h*fdy(i)
fz1(i)=h*fdz(i)
fw1(i)=h*fdw(i)
!=========================
x1(i)=x(i)+0.5*kx1(i)
y1(i)=y(i)+0.5*ky1(i)
z1(i)=z(i)+0.5*kz1(i)
w1(i)=w(i)+0.5*kw1(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx2(i)=h*fx(i)
ky2(i)=h*fy(i)
kz2(i)=h*fz(i)
kw2(i)=h*fw(i)
dx1(i)=dx(i)+0.5*fx1(i)
dy1(i)=dy(i)+0.5*fy1(i)
dz1(i)=dz(i)+0.5*fz1(i)
dw1(i)=dw(i)+0.5*fw1(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx2(i)=h*fdx(i)
fy2(i)=h*fdy(i)
fz2(i)=h*fdz(i)
fw2(i)=h*fdw(i)
!=========================
x1(i)=x(i)+0.5*kx2(i)
y1(i)=y(i)+0.5*ky2(i)
z1(i)=z(i)+0.5*kz2(i)
w1(i)=w(i)+0.5*kw2(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx3(i)=h*fx(i)
ky3(i)=h*fy(i)
kz3(i)=h*fz(i)
kw3(i)=h*fw(i)
dx1(i)=dx(i)+0.5*fx2(i)
dy1(i)=dy(i)+0.5*fy2(i)
dz1(i)=dz(i)+0.5*fz2(i)
dw1(i)=dw(i)+0.5*fw2(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx3(i)=h*fdx(i)
fy3(i)=h*fdy(i)
fz3(i)=h*fdz(i)
fw3(i)=h*fdw(i)
!=========================
x1(i)=x(i)+kx3(i)
y1(i)=y(i)+ky3(i)
z1(i)=z(i)+kz3(i)
w1(i)=w(i)+kw3(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx4(i)=h*fx(i)
ky4(i)=h*fy(i)
kz4(i)=h*fz(i)
kw4(i)=h*fw(i)
dx1(i)=dx(i)+fx3(i)
dy1(i)=dy(i)+fy3(i)
dz1(i)=dz(i)+fz3(i)
dw1(i)=dw(i)+fw3(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx4(i)=h*fdx(i)
fy4(i)=h*fdy(i)
fz4(i)=h*fdz(i)
fw4(i)=h*fdw(i)
!=========================
x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0
y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0
z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0
w(i)=w(i)+(kw1(i)+2.0*kw2(i)+2.0*kw3(i)+kw4(i))/6.0
dx(i)=dx(i)+(fx1(i)+2.0*fx2(i)+2.0*fx3(i)+fx4(i))/6.0
dy(i)=dy(i)+(fy1(i)+2.0*fy2(i)+2.0*fy3(i)+fy4(i))/6.0
dz(i)=dz(i)+(fz1(i)+2.0*fz2(i)+2.0*fz3(i)+fz4(i))/6.0
dw(i)=dw(i)+(fw1(i)+2.0*fw2(i)+2.0*fw3(i)+fw4(i))/6.0
end do
return
end subroutine
!=========================
subroutine fun1(x,y,z,w,dx,dy,dz,dw,fdx,fdy,fdz,fdw,i)
implicit none
real*8::dx,dy,dz,dw,coupling
real*8::x,y,z,w
real*8::fdx,fdy,fdz,fdw
real*8::a=10.0,b=8.0/3.0,r=24.8
integer :: i,j
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)
end do
fdx=a*(dy-dx)+epsilon_2*E(i)*dw
fdy=(r-z)*dx-dy-x*dz
fdz=y*dx+x*dy-b*dz+(epsilon_1/real(M-1))*coupling*dz
fdw=-K*dw-epsilon_2*E(i)*dx
endsubroutine
!=========================
subroutine fun(x,y,z1,w,fx,fy,fz,fw,i)
real*8::x,y,z1,w,fx,fy,fz,fw,coupling
real*8::a,b,r
integer :: i,j
a=10.0
b=8.0/3.0
r=24.8
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(z(j)-z(i))
end do
fx=a*(y-x)+epsilon_2*E(i)*w
fy=r*x-y-x*z1
fz=x*y-b*z1+(epsilon_1/real(M-1))*coupling
fw=-K*w-epsilon_2*E(i)*(x-BB)
end subroutine
!=========================
!=========================
subroutine lorenz(x,y,z,w)
implicit none
integer :: i
real*8::x(M),y(M),z(M),w(M)
real*8::x1(M),y1(M),z1(M),w1(M)
real*8::kx1(M),kx2(M),kx3(M),kx4(M)
real*8::ky1(M),ky2(M),ky3(M),ky4(M)
real*8::kz1(M),kz2(M),kz3(M),kz4(M)
real*8::kw1(M),kw2(M),kw3(M),kw4(M)
real*8::fx(M),fy(M),fz(M),fw(M)
x1=x
y1=y
z1=z
w1=w
do i=1,M,1
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx1(i)=h*fx(i)
ky1(i)=h*fy(i)
kz1(i)=h*fz(i)
kw1(i)=h*fw(i)
x1(i)=x(i)+0.5*kx1(i)
y1(i)=y(i)+0.5*ky1(i)
z1(i)=z(i)+0.5*kz1(i)
w1(i)=w(i)+0.5*kw1(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx2(i)=h*fx(i)
ky2(i)=h*fy(i)
kz2(i)=h*fz(i)
kw2(i)=h*fw(i)
x1(i)=x(i)+0.5*kx2(i)
y1(i)=y(i)+0.5*ky2(i)
z1(i)=z(i)+0.5*kz2(i)
w1(i)=w(i)+0.5*kw2(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx3(i)=h*fx(i)
ky3(i)=h*fy(i)
kz3(i)=h*fz(i)
kw3(i)=h*fw(i)
x1(i)=x(i)+kx3(i)
y1(i)=y(i)+ky3(i)
z1(i)=z(i)+kz3(i)
w1(i)=w(i)+kw3(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx4(i)=h*fx(i)
ky4(i)=h*fy(i)
kz4(i)=h*fz(i)
kw4(i)=h*fw(i)
x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0d0
y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0d0
z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0d0
w(i)=w(i)+(kw1(i)+2.0*kw2(i)+2.0*kw3(i)+kw4(i))/6.0d0
end do
return
end subroutine
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(20,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(20,*)
end do
return
end subroutine neighbour
!Umax与Umin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real*8 :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
end module Lorenz_Control
program main
use Lorenz_Control
implicit none
integer*4::i,ii,j,t
real*8::x1,x2,x3
real*8::lay(M),X_max(M),X_min(M)
open(10,file="k_lay_G-.txt")
open(11,file="k_lay_G+.txt")
open(12,file="k_lay_G0.txt")
open(13,file="k_lay.txt")
open(20,file="neighbour_matrix.txt")
call neighbour()
E=1.0
DO j=1,301,1
epsilon_2=j*0.01-0.01
!=========================
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i)=int(x1*40.0-20.0)
y(i)=int(x2*50.0-25.0)
z(i)=int(x3*45.0)
end do
X_max=-1000.0
X_min=1000.0
DO t=1,100000,1
call lorenz(x,y,z,w)
if(t>90000) then
call X_max_min(x(:),X_max,X_min)
end if
ENDDO
dx=d0
dy=0.0
dz=0.0
dw=0.0
!=========================
lay=0
DO i=1,2000000
call msf(x,y,z,w,dx,dy,dz,dw)
dx1=dx
dy1=dy
dz1=dz
dw1=dw
do ii=1,M,1
lay(ii)=lay(ii)+log((sqrt(dx(ii)**2+dy(ii)**2+dz(ii)**2+dw(ii)**2))/d0)
dx(ii)=d0*dx(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
dy(ii)=d0*dy(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
dz(ii)=d0*dz(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
dw(ii)=d0*dw(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
end do
ENDDO
do i=1,M,1
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G-
write(10,*) i,epsilon_2,lay(i)/2000000.0/0.01
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
write(11,*) i,epsilon_2,lay(i)/2000000.0/0.01
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
write(12,*) i,epsilon_2,lay(i)/2000000.0/0.01
end if
write(13,*) epsilon_2,lay(10)/2000000.0/0.01
write(*,*) epsilon_2,lay(i)/2000000.0/0.01
end do
ENDDO
close(10)
close(11)
close(12)
close(13)
close(20)
deallocate(neighbour_matrix)
end program main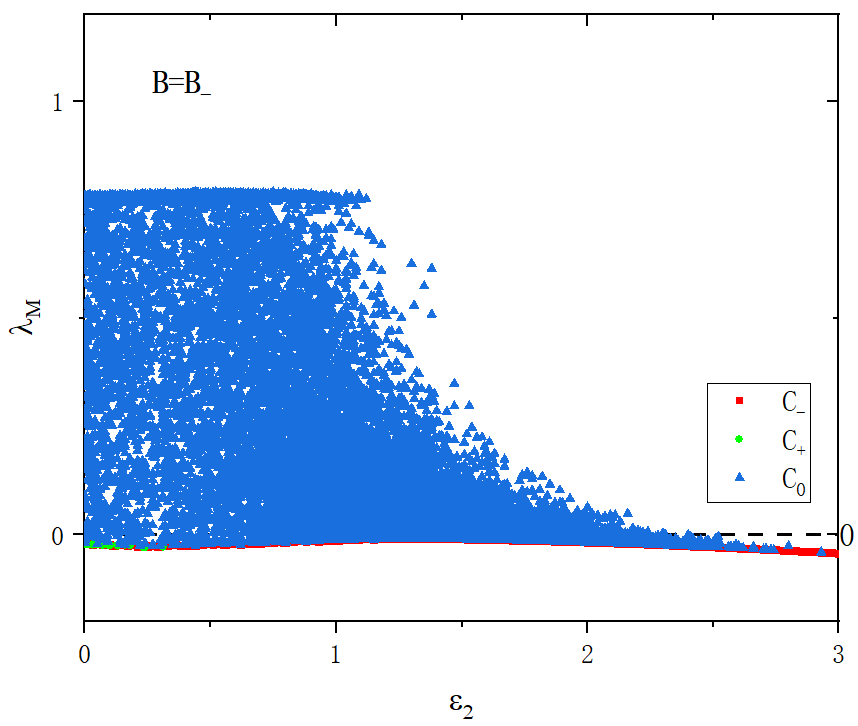
figure 7_C

figure 7_D
module Lorenz_Control
implicit none
real,parameter :: h=0.01
integer,parameter :: M=100
real*8::dx(M),dy(M),dz(M),dw(M),x(M),y(M),z(M),w(M)
real*8::dx1(M),dy1(M),dz1(M),dw1(M)
real*8::epsilon_1=0.08,epsilon_2
real*8::d0=1.0e-6,BB=0.0,E(M),K=3.0
integer,allocatable :: neighbour_matrix(:,:)
contains
!=========================
subroutine msf(x,y,z,w,dx,dy,dz,dw)
implicit none
integer :: i
real*8::x(M),y(M),z(M),w(M)
real*8::x1(M),y1(M),z1(M),w1(M)
real*8::fx(M),fy(M),fz(M),fw(M)
real*8::kx1(M),kx2(M),kx3(M),kx4(M)
real*8::ky1(M),ky2(M),ky3(M),ky4(M)
real*8::kz1(M),kz2(M),kz3(M),kz4(M)
real*8::kw1(M),kw2(M),kw3(M),kw4(M)
real*8::dx(M),dy(M),dz(M),dw(M)
real*8::dx1(M),dy1(M),dz1(M),dw1(M)
real*8::fdx(M),fdy(M),fdz(M),fdw(M)
real*8::fx1(M),fx2(M),fx3(M),fx4(M)
real*8::fy1(M),fy2(M),fy3(M),fy4(M)
real*8::fz1(M),fz2(M),fz3(M),fz4(M)
real*8::fw1(M),fw2(M),fw3(M),fw4(M)
!=========================
x1=x
y1=y
z1=z
w1=w
do i=1,M,1
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx1(i)=h*fx(i)
ky1(i)=h*fy(i)
kz1(i)=h*fz(i)
kw1(i)=h*fw(i)
dx1(i)=dx(i)
dy1(i)=dy(i)
dz1(i)=dz(i)
dw1(i)=dw(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx1(i)=h*fdx(i)
fy1(i)=h*fdy(i)
fz1(i)=h*fdz(i)
fw1(i)=h*fdw(i)
!=========================
x1(i)=x(i)+0.5*kx1(i)
y1(i)=y(i)+0.5*ky1(i)
z1(i)=z(i)+0.5*kz1(i)
w1(i)=w(i)+0.5*kw1(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx2(i)=h*fx(i)
ky2(i)=h*fy(i)
kz2(i)=h*fz(i)
kw2(i)=h*fw(i)
dx1(i)=dx(i)+0.5*fx1(i)
dy1(i)=dy(i)+0.5*fy1(i)
dz1(i)=dz(i)+0.5*fz1(i)
dw1(i)=dw(i)+0.5*fw1(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx2(i)=h*fdx(i)
fy2(i)=h*fdy(i)
fz2(i)=h*fdz(i)
fw2(i)=h*fdw(i)
!=========================
x1(i)=x(i)+0.5*kx2(i)
y1(i)=y(i)+0.5*ky2(i)
z1(i)=z(i)+0.5*kz2(i)
w1(i)=w(i)+0.5*kw2(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx3(i)=h*fx(i)
ky3(i)=h*fy(i)
kz3(i)=h*fz(i)
kw3(i)=h*fw(i)
dx1(i)=dx(i)+0.5*fx2(i)
dy1(i)=dy(i)+0.5*fy2(i)
dz1(i)=dz(i)+0.5*fz2(i)
dw1(i)=dw(i)+0.5*fw2(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx3(i)=h*fdx(i)
fy3(i)=h*fdy(i)
fz3(i)=h*fdz(i)
fw3(i)=h*fdw(i)
!=========================
x1(i)=x(i)+kx3(i)
y1(i)=y(i)+ky3(i)
z1(i)=z(i)+kz3(i)
w1(i)=w(i)+kw3(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx4(i)=h*fx(i)
ky4(i)=h*fy(i)
kz4(i)=h*fz(i)
kw4(i)=h*fw(i)
dx1(i)=dx(i)+fx3(i)
dy1(i)=dy(i)+fy3(i)
dz1(i)=dz(i)+fz3(i)
dw1(i)=dw(i)+fw3(i)
call fun1(x1(i),y1(i),z1(i),w1(i),dx1(i),dy1(i),dz1(i),dw1(i),fdx(i),fdy(i),fdz(i),fdw(i),i)
fx4(i)=h*fdx(i)
fy4(i)=h*fdy(i)
fz4(i)=h*fdz(i)
fw4(i)=h*fdw(i)
!=========================
x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0
y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0
z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0
w(i)=w(i)+(kw1(i)+2.0*kw2(i)+2.0*kw3(i)+kw4(i))/6.0
dx(i)=dx(i)+(fx1(i)+2.0*fx2(i)+2.0*fx3(i)+fx4(i))/6.0
dy(i)=dy(i)+(fy1(i)+2.0*fy2(i)+2.0*fy3(i)+fy4(i))/6.0
dz(i)=dz(i)+(fz1(i)+2.0*fz2(i)+2.0*fz3(i)+fz4(i))/6.0
dw(i)=dw(i)+(fw1(i)+2.0*fw2(i)+2.0*fw3(i)+fw4(i))/6.0
end do
return
end subroutine
!=========================
subroutine fun1(x,y,z,w,dx,dy,dz11,dw,fdx,fdy,fdz,fdw,i)
implicit none
real*8::dx,dy,dz11,dw,coupling
real*8::x,y,z,w
real*8::fdx,fdy,fdz,fdw
real*8::a=10.0,b=8.0/3.0,r=24.8
integer :: i,j
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(dz(j)-dz(i))
end do
fdx=a*(dy-dx)+epsilon_2*E(i)*dw
fdy=(r-z)*dx-dy-x*dz11
fdz=y*dx+x*dy-b*dz11+(epsilon_1/real(M-1))*coupling
fdw=-K*dw-epsilon_2*E(i)*dx
endsubroutine
!=========================
subroutine fun(x,y,z1,w,fx,fy,fz,fw,i)
real*8::x,y,z1,w,fx,fy,fz,fw,coupling
real*8::a,b,r
integer :: i,j
a=10.0
b=8.0/3.0
r=24.8
coupling=0.0
do j=1,M,1
coupling=coupling+neighbour_matrix(i,j)*(z(j)-z(i))
end do
fx=a*(y-x)+epsilon_2*E(i)*w
fy=r*x-y-x*z1
fz=x*y-b*z1+(epsilon_1/real(M-1))*coupling
fw=-K*w-epsilon_2*E(i)*(x-BB)
end subroutine
!=========================
!=========================
subroutine lorenz(x,y,z,w)
implicit none
integer :: i
real*8::x(M),y(M),z(M),w(M)
real*8::x1(M),y1(M),z1(M),w1(M)
real*8::kx1(M),kx2(M),kx3(M),kx4(M)
real*8::ky1(M),ky2(M),ky3(M),ky4(M)
real*8::kz1(M),kz2(M),kz3(M),kz4(M)
real*8::kw1(M),kw2(M),kw3(M),kw4(M)
real*8::fx(M),fy(M),fz(M),fw(M)
x1=x
y1=y
z1=z
w1=w
do i=1,M,1
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx1(i)=h*fx(i)
ky1(i)=h*fy(i)
kz1(i)=h*fz(i)
kw1(i)=h*fw(i)
x1(i)=x(i)+0.5*kx1(i)
y1(i)=y(i)+0.5*ky1(i)
z1(i)=z(i)+0.5*kz1(i)
w1(i)=w(i)+0.5*kw1(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx2(i)=h*fx(i)
ky2(i)=h*fy(i)
kz2(i)=h*fz(i)
kw2(i)=h*fw(i)
x1(i)=x(i)+0.5*kx2(i)
y1(i)=y(i)+0.5*ky2(i)
z1(i)=z(i)+0.5*kz2(i)
w1(i)=w(i)+0.5*kw2(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx3(i)=h*fx(i)
ky3(i)=h*fy(i)
kz3(i)=h*fz(i)
kw3(i)=h*fw(i)
x1(i)=x(i)+kx3(i)
y1(i)=y(i)+ky3(i)
z1(i)=z(i)+kz3(i)
w1(i)=w(i)+kw3(i)
call fun(x1(i),y1(i),z1(i),w1(i),fx(i),fy(i),fz(i),fw(i),i)
kx4(i)=h*fx(i)
ky4(i)=h*fy(i)
kz4(i)=h*fz(i)
kw4(i)=h*fw(i)
x(i)=x(i)+(kx1(i)+2.0*kx2(i)+2.0*kx3(i)+kx4(i))/6.0d0
y(i)=y(i)+(ky1(i)+2.0*ky2(i)+2.0*ky3(i)+ky4(i))/6.0d0
z(i)=z(i)+(kz1(i)+2.0*kz2(i)+2.0*kz3(i)+kz4(i))/6.0d0
w(i)=w(i)+(kw1(i)+2.0*kw2(i)+2.0*kw3(i)+kw4(i))/6.0d0
end do
return
end subroutine
!建立网络结构:全局耦合
subroutine neighbour()
implicit none
integer :: i,j,number
allocate(neighbour_matrix(M,M))
!初始化网络矩阵
neighbour_matrix=0
do i=1,M-1,1
do j=i+1,M,1
neighbour_matrix(i,j)=1
neighbour_matrix(j,i)=1
end do
end do
!输出矩阵
do i=1,M,1
do j=1,M,1
write(20,"(I2)",advance='no') neighbour_matrix(i,j)
end do
write(20,*)
end do
return
end subroutine neighbour
!Umax与Umin
subroutine X_max_min(xxx,X_max,X_min)
implicit none
real*8 :: X_max(M),X_min(M),xxx(M)
integer :: i
do i=1,M,1
if(X_max(i)<xxx(i)) then
X_max(i)=xxx(i)
end if
if(X_min(i)>xxx(i)) then
X_min(i)=xxx(i)
end if
end do
return
end subroutine X_max_min
end module Lorenz_Control
program main
use Lorenz_Control
implicit none
integer*4::i,ii,j,t
real*8::x1,x2,x3
real*8::lay(M),X_max(M),X_min(M)
open(10,file="k_lay_G-.txt")
open(11,file="k_lay_G+.txt")
open(12,file="k_lay_G0.txt")
open(13,file="k_lay.txt")
open(20,file="neighbour_matrix.txt")
call neighbour()
E=1.0
DO j=1,301,10
epsilon_2=j*0.01-0.01
!=========================
do i=1,M,1
call random_number(x1)
call random_number(x2)
call random_number(x3)
x(i)=int(x1*40.0-20.0)
y(i)=int(x2*50.0-25.0)
z(i)=int(x3*45.0)
w(i)=1.0
end do
X_max=-1000.0
X_min=1000.0
DO t=1,100000,1
call lorenz(x,y,z,w)
if(t>90000) then
call X_max_min(x(:),X_max,X_min)
end if
ENDDO
dx=d0
dy=0.0
dz=0.0
dw=0.0
!=========================
lay=0
DO i=1,2000000
call msf(x,y,z,w,dx,dy,dz,dw)
dx1=dx
dy1=dy
dz1=dz
dw1=dw
do ii=1,M,1
lay(ii)=lay(ii)+log((sqrt(dx(ii)**2+dy(ii)**2+dz(ii)**2+dw(ii)**2))/d0)
dx(ii)=d0*dx(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
dy(ii)=d0*dy(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
dz(ii)=d0*dz(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
dw(ii)=d0*dw(ii)/sqrt(dx1(ii)**2+dy1(ii)**2+dz1(ii)**2+dw1(ii)**2)
end do
ENDDO
do i=1,M,1
if(abs(X_max(i)-X_min(i))<5.0.and.X_max(i)<0) then
!G-
write(10,*) i,epsilon_2,lay(i)/2000000.0/0.01
else if(abs(X_max(i)-X_min(i))<5.0.and.X_min(i)>0) then
!G+
write(11,*) i,epsilon_2,lay(i)/2000000.0/0.01
else if(X_max(i)-X_min(i)>5.0.and.X_min(i)<0.and.X_max(i)>0) then
!G0
write(12,*) i,epsilon_2,lay(i)/2000000.0/0.01
end if
write(13,*) epsilon_2,lay(10)/2000000.0/0.01
write(*,*) epsilon_2,lay(i)/2000000.0/0.01
end do
ENDDO
close(10)
close(11)
close(12)
close(13)
close(20)
deallocate(neighbour_matrix)
end program main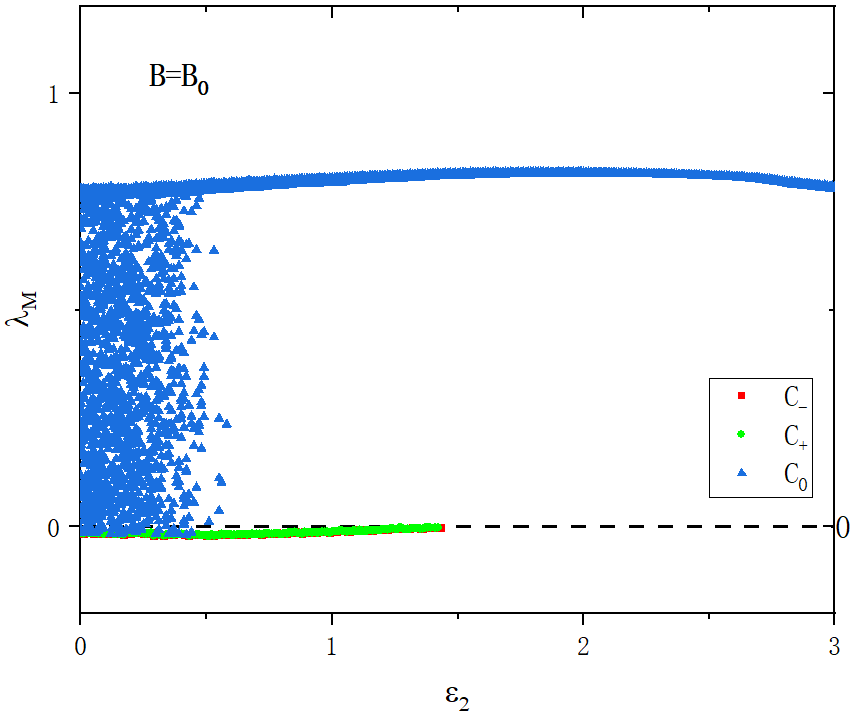
figure 8

figure 8_A
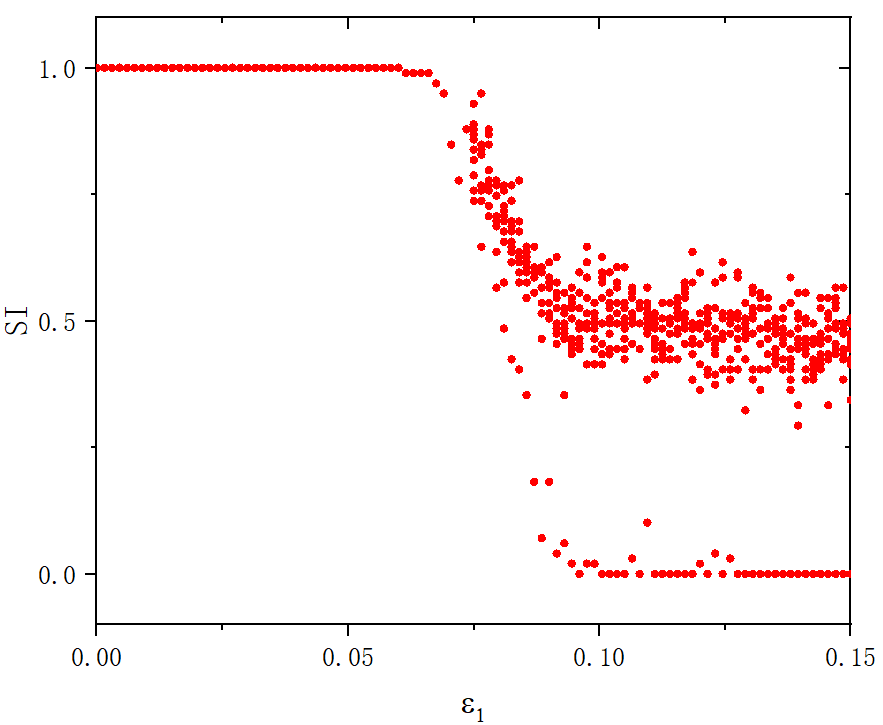
figure 8_B
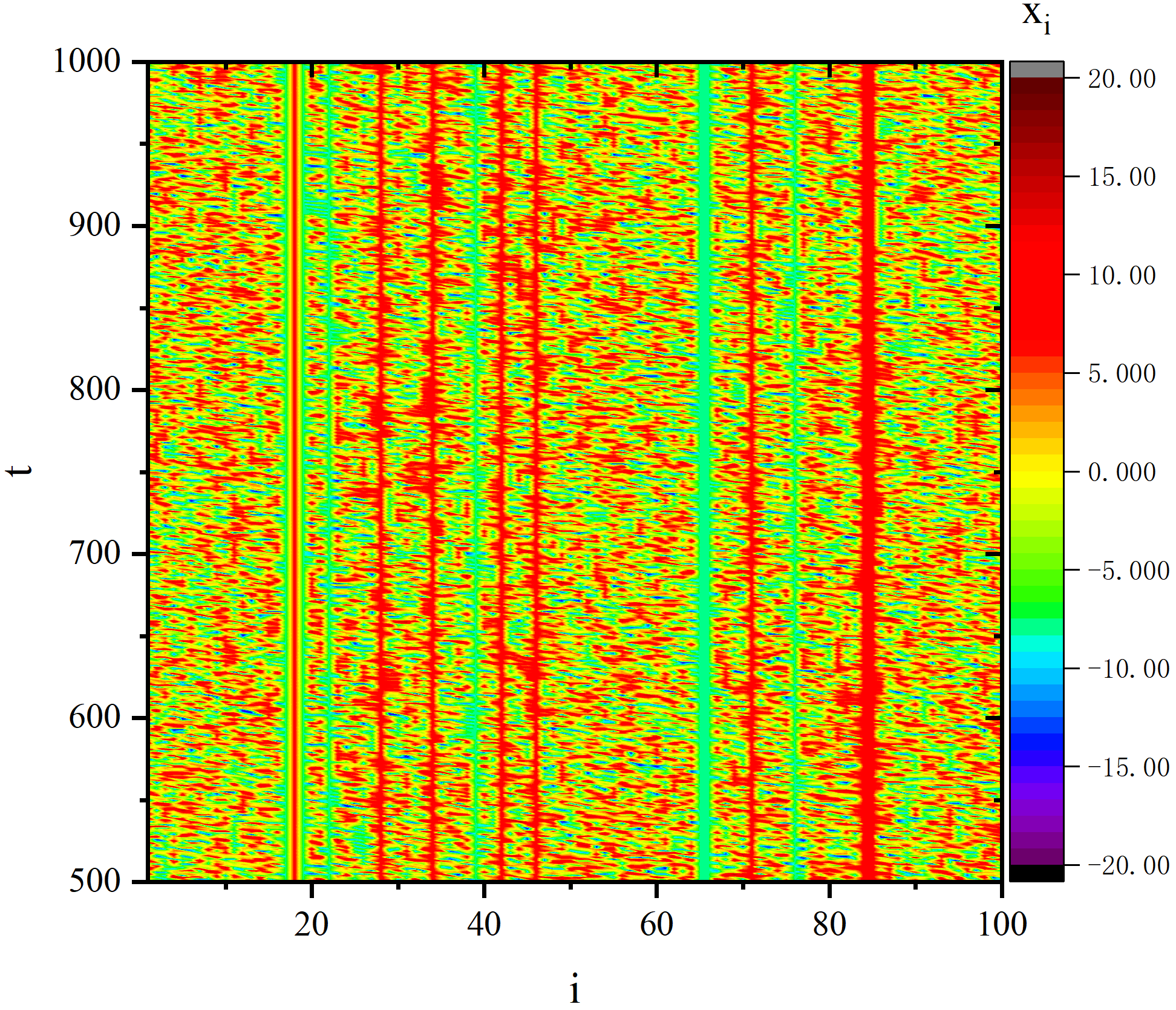

figure 8_C
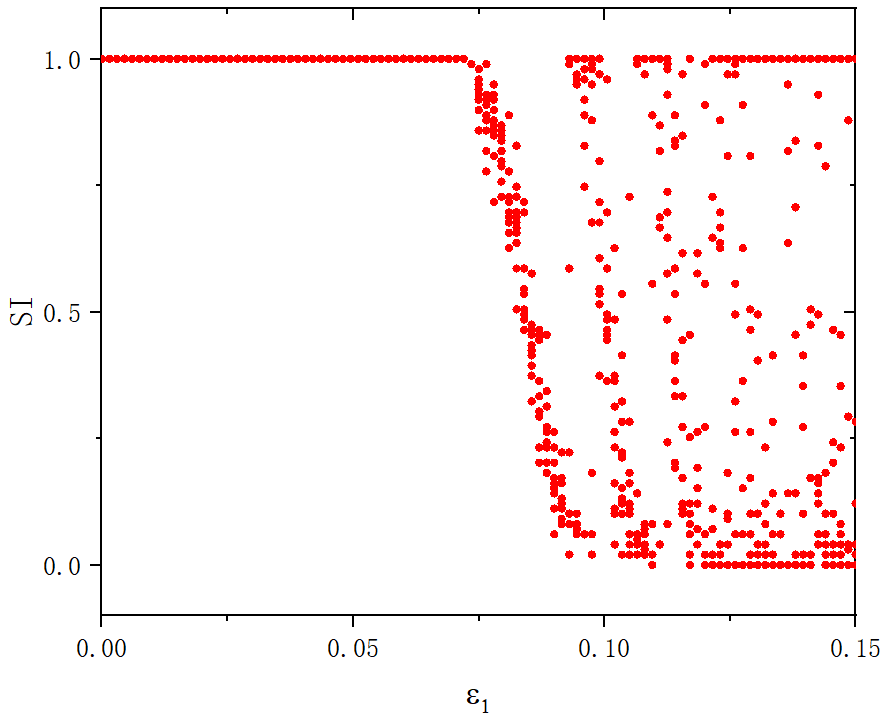
figure 8_D


figure 9
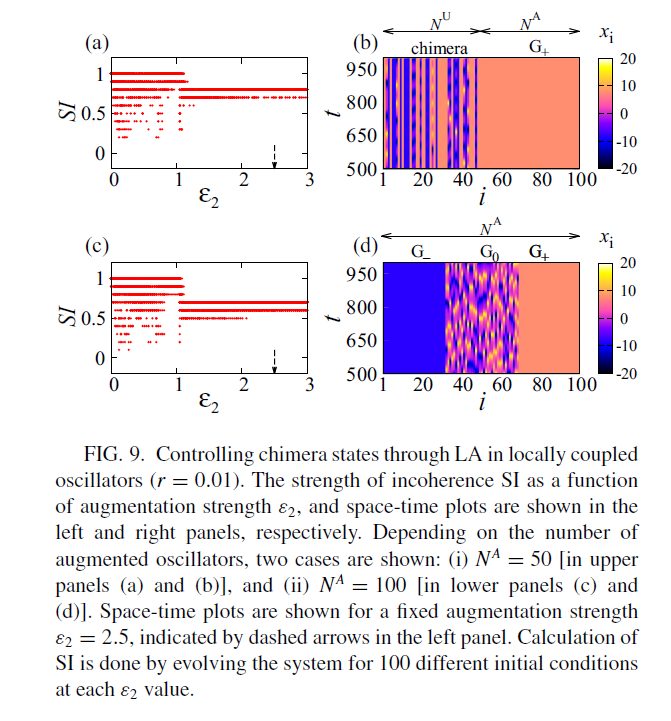
figure 9_A

figure 9_B
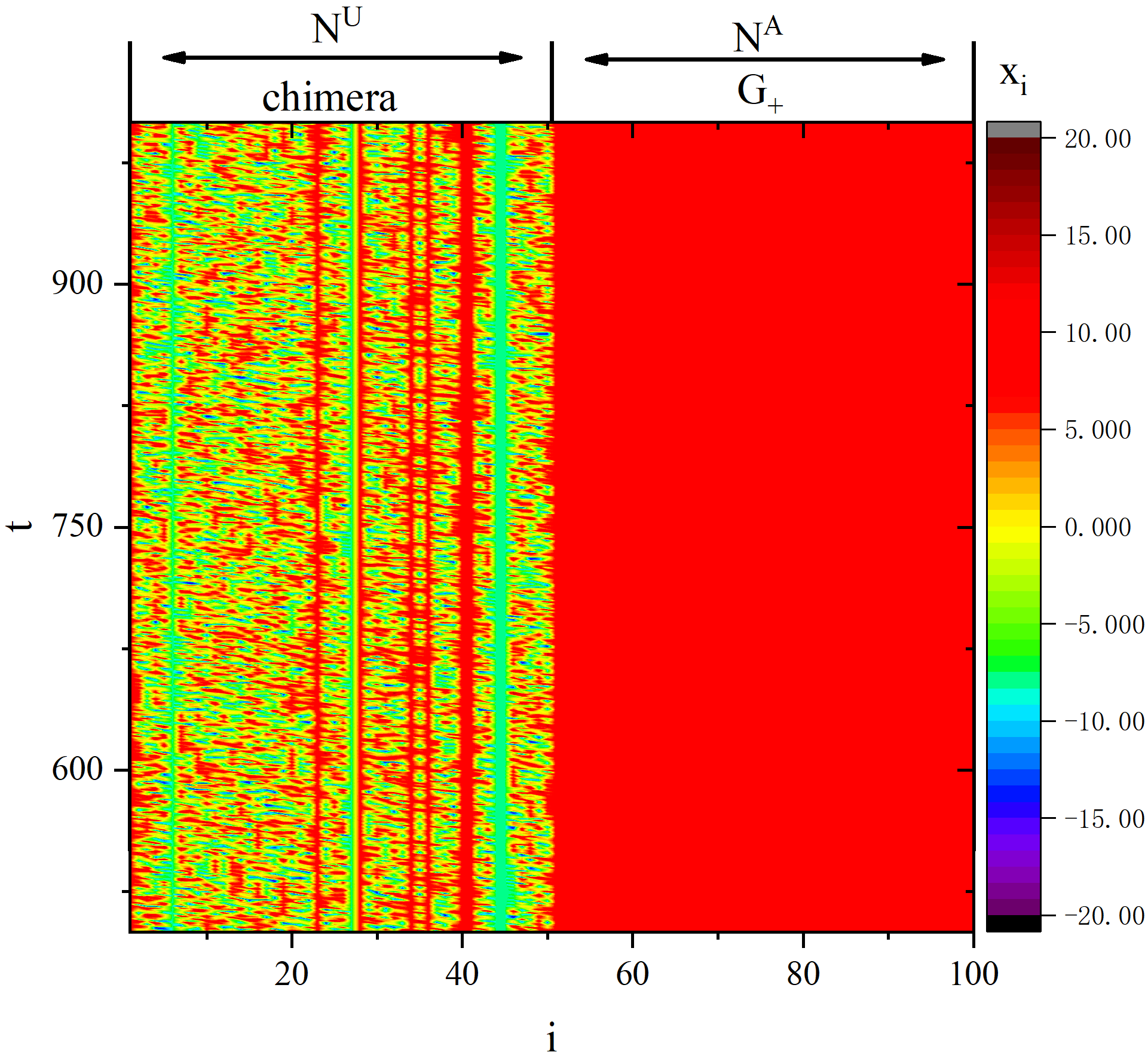
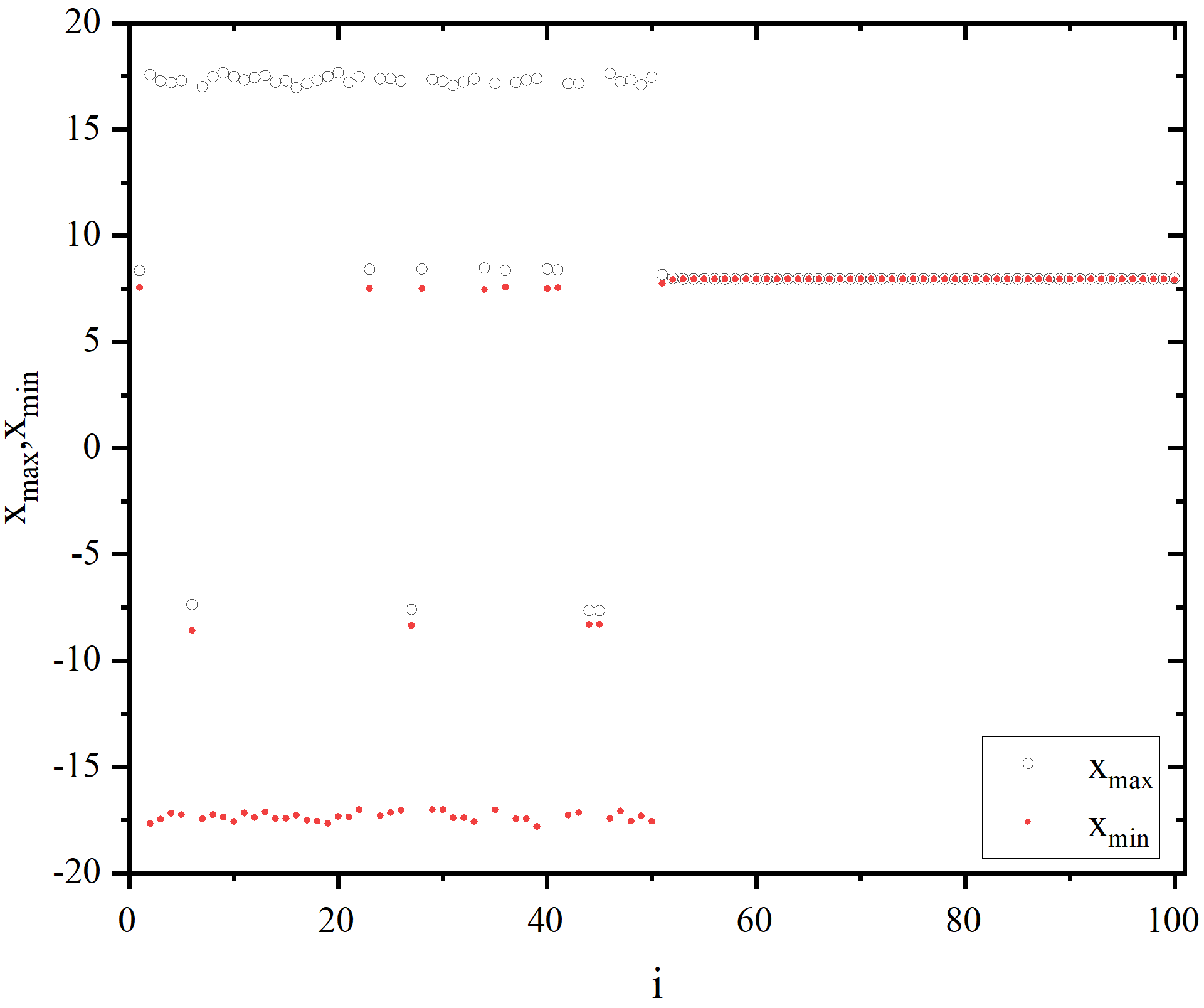
figure 9_C
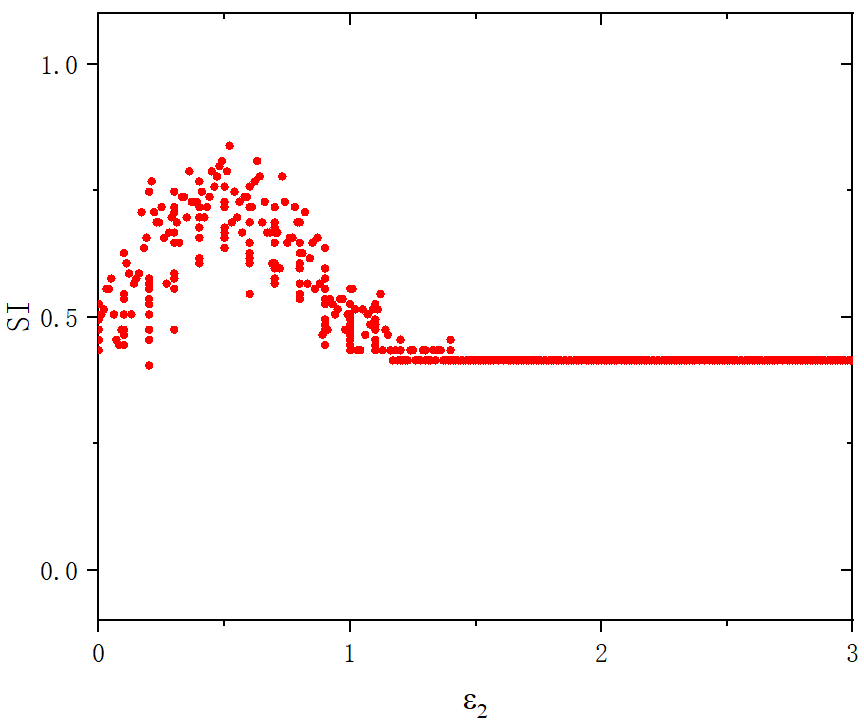
figure 9_D
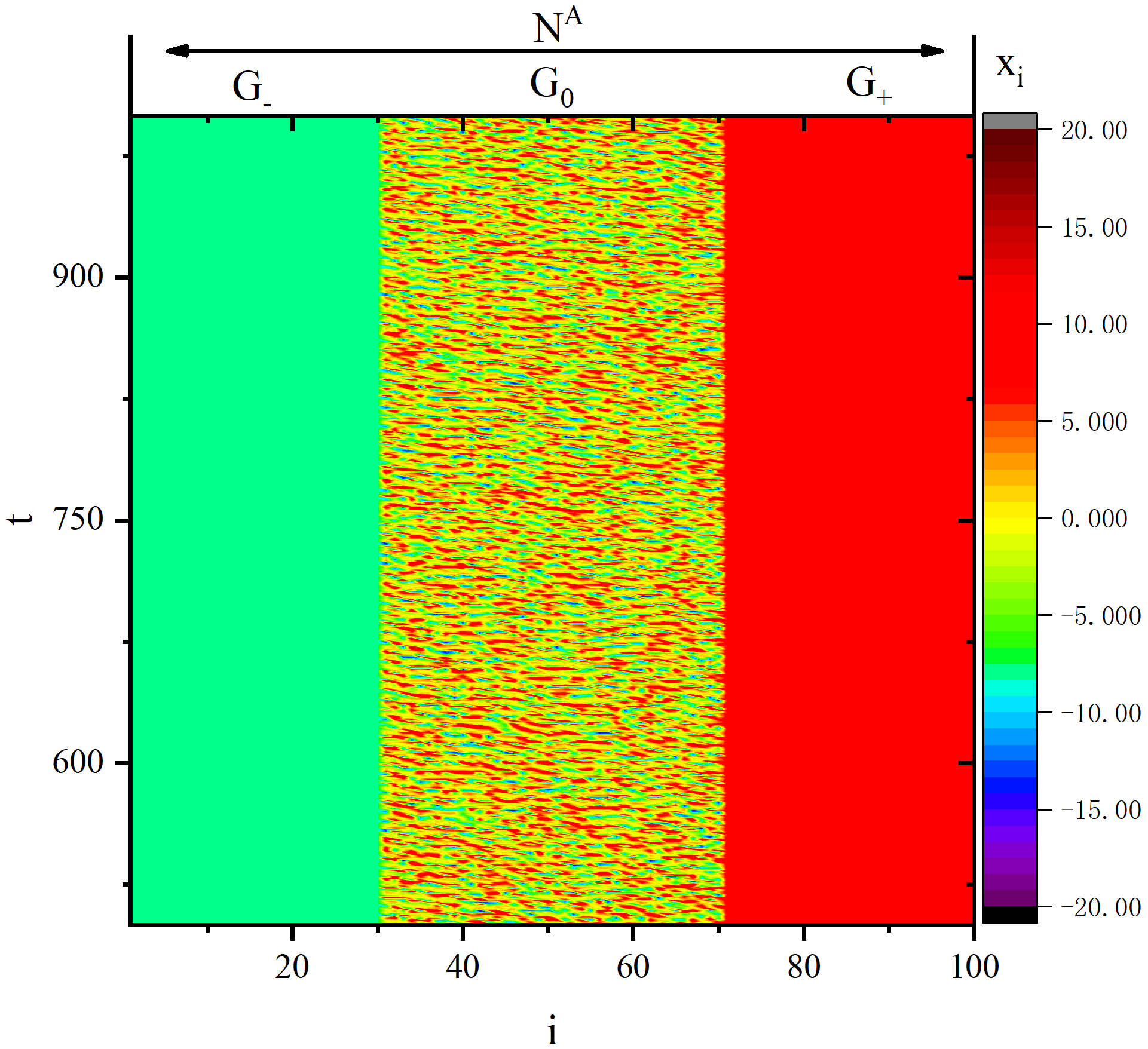
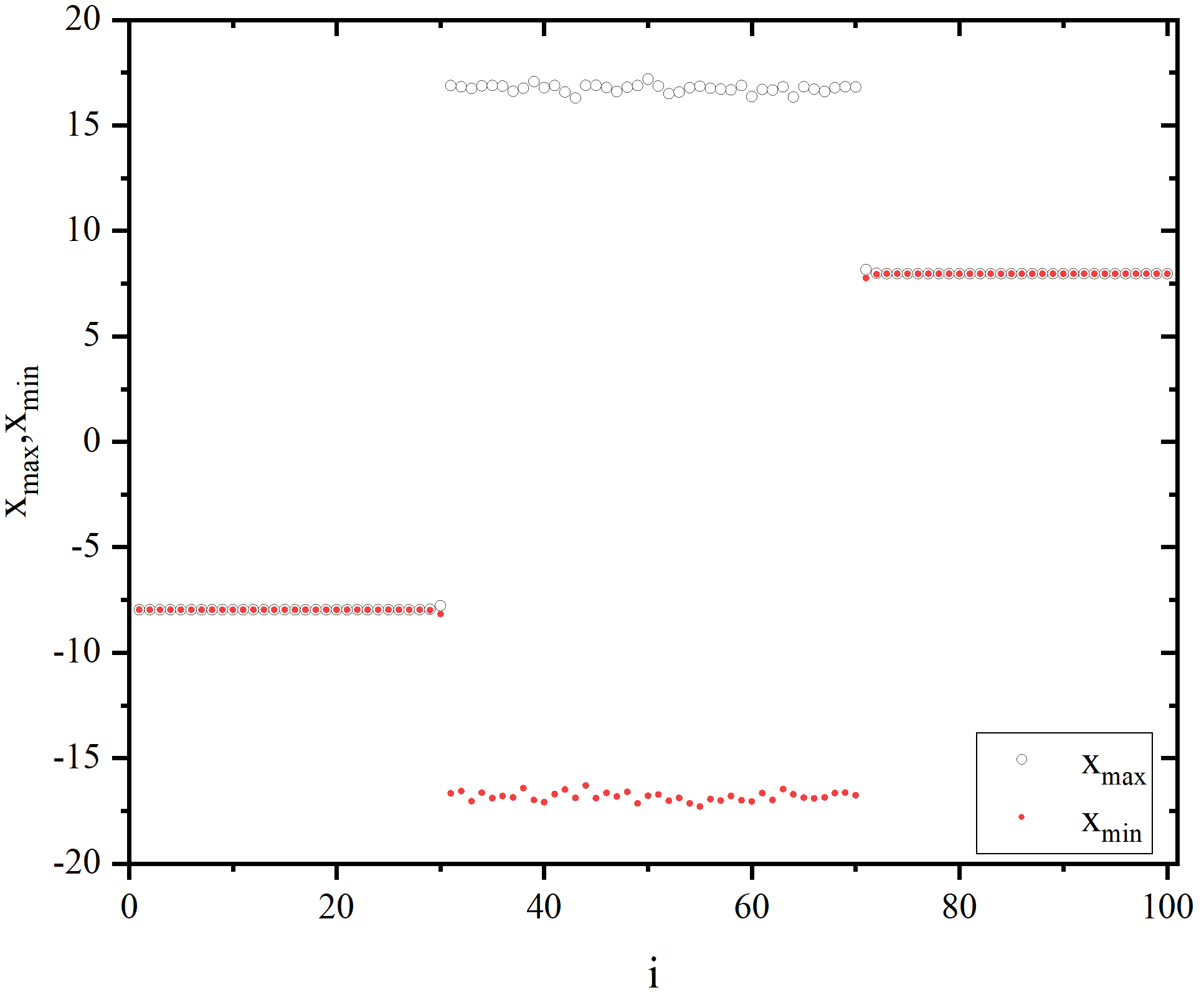
figure 10
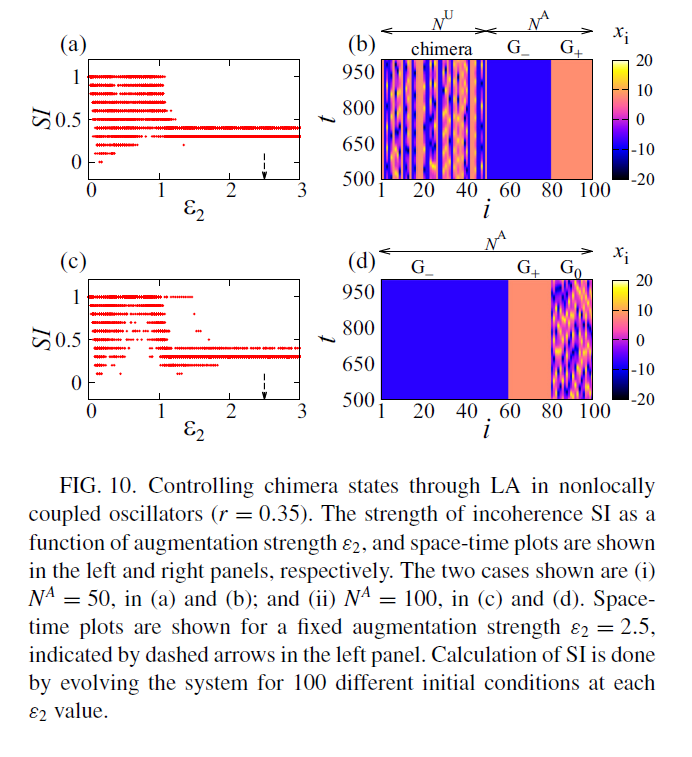
figure 10_A

figure 10_B
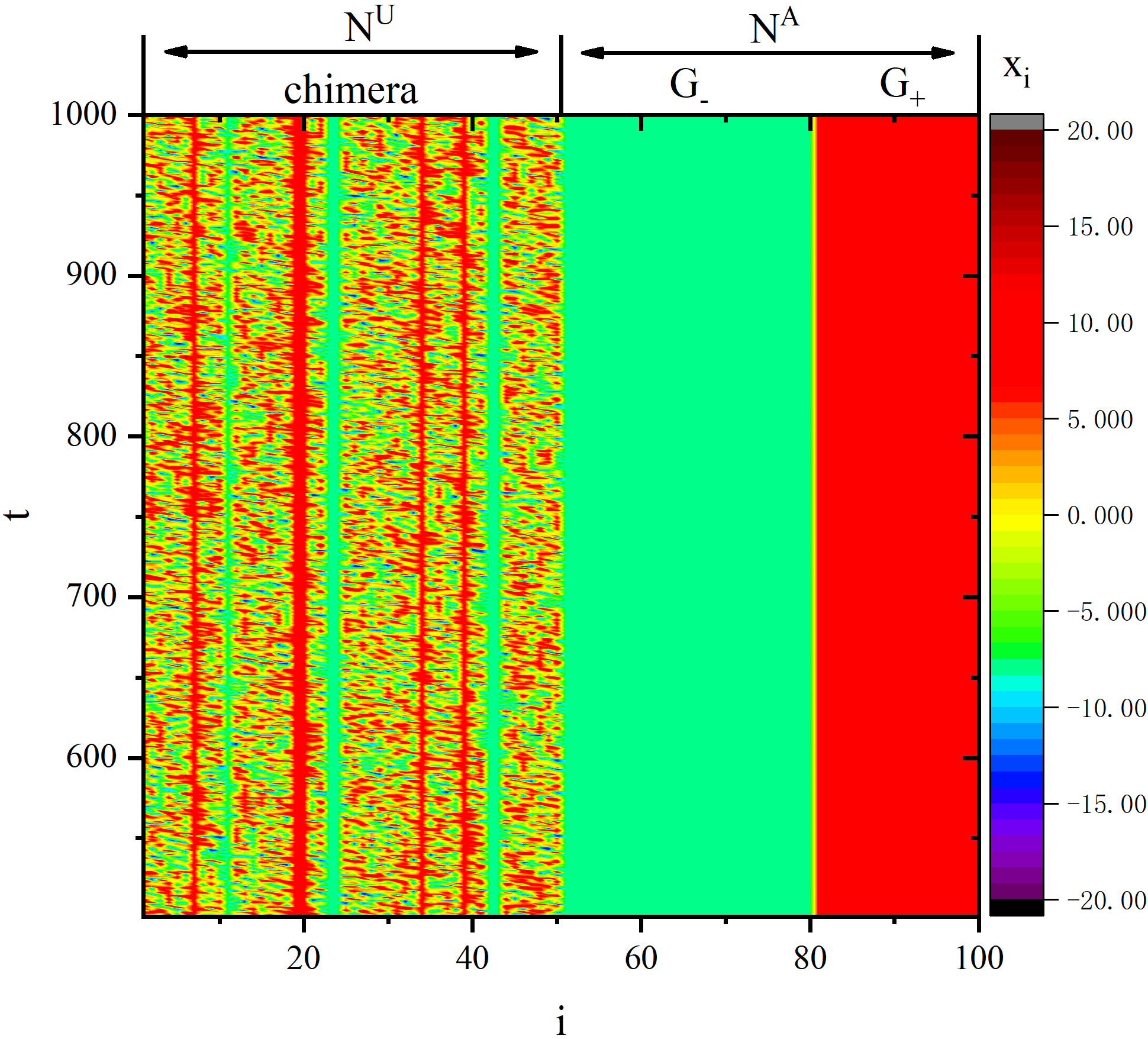

figure 10_C
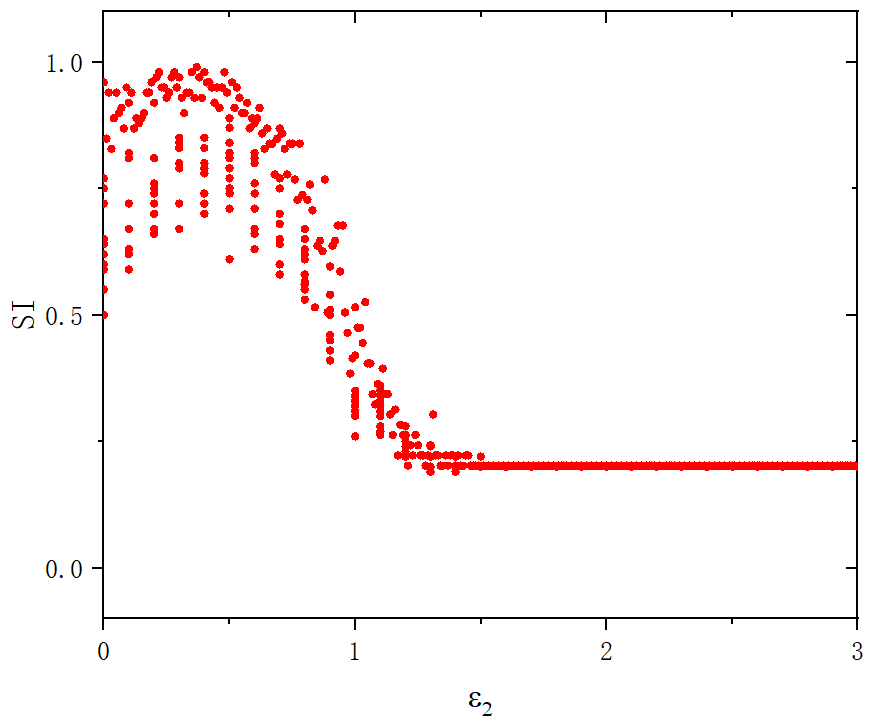
figure 10_D