深度学习

• 层次化的概念让计算机构建较简单的概念来学习复杂概念。如果绘制出表示这些概念如何建立在彼此之上的一幅图，我们将得到一张“深”（层次很多）的图。由此，我们称这种方法为AI深度学习(deep learning)。

数学符号

第一章 引言

1.1 本书面向的读者

1.2 深度学习的历史趋势

• 深度学习的三架马车：算力、数据、算法

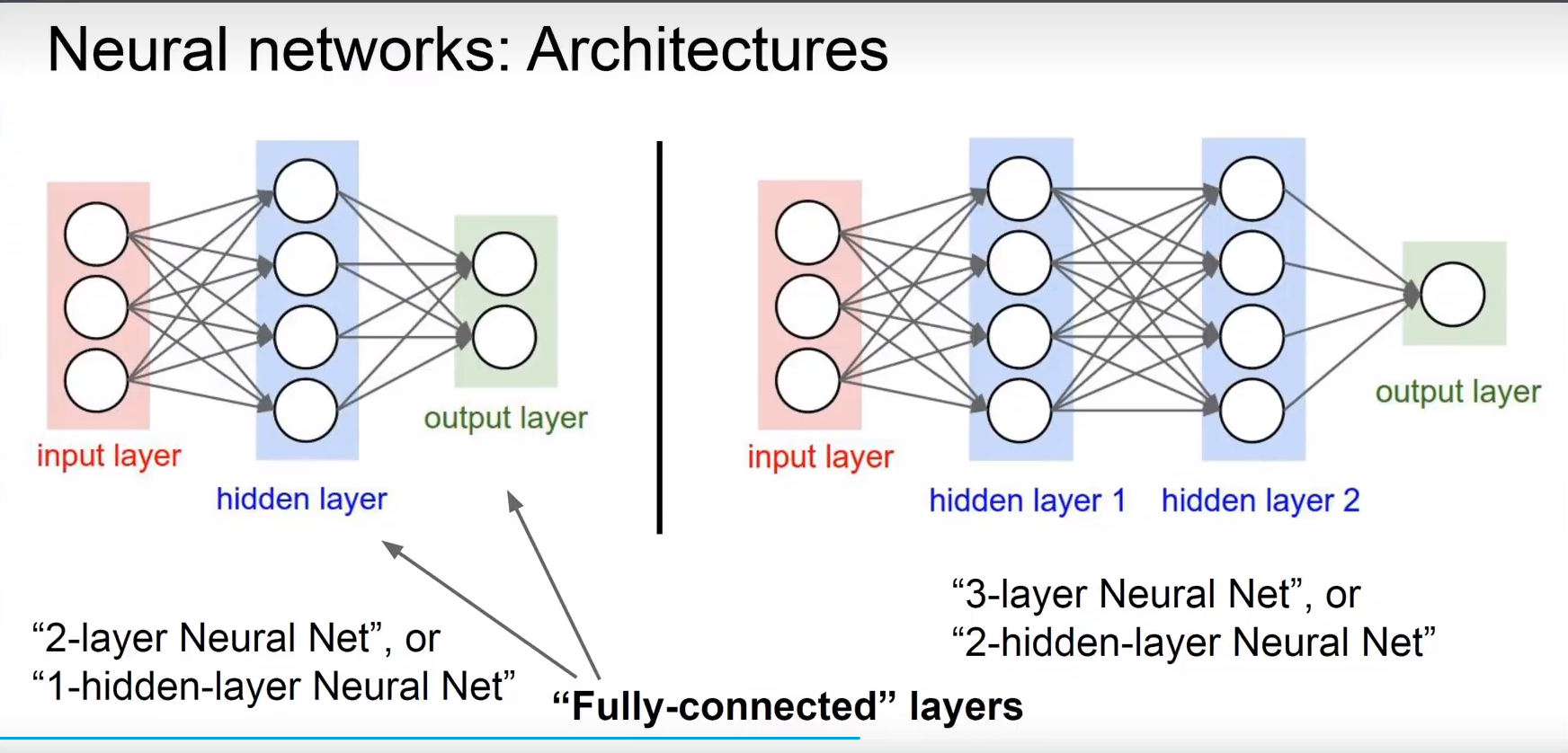
1.2.1 神经网络的众多名称和命运变迁

1.2.2 与日俱增的数据量

1.2.3 与日俱增的模型规模

1.2.4 与日俱增的精度、复杂度和对现实世界的冲击

参考资料

• 花书解读：https://www.bilibili.com/video/BV1kE4119726?p=1&vd_source=806d6762f81929994d4549f36fc78211

第一部分 应用数学与机器学习基础

第二章 线性代数

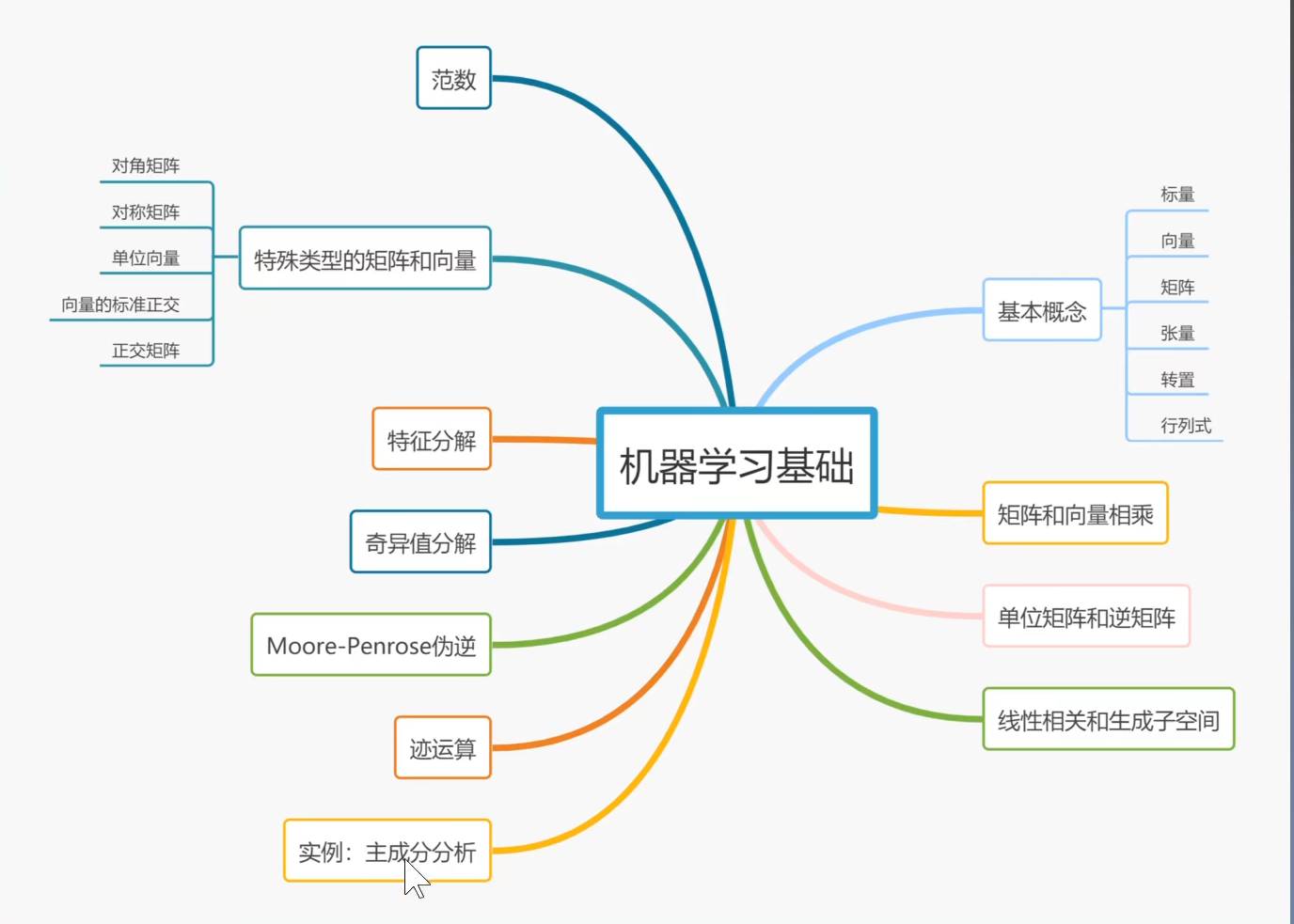
2.1 标量、向量、矩阵和张量

• 标量：一个数
• 向量：一行数或一列数
• 矩阵：二维数组
• 张量：多个矩阵
• 转置：作用于矩阵，行变列，列变行

2.2 矩阵和向量相乘

• 向量和矩阵相乘，向量需满足矩阵的行数
• 标量和矩阵相乘，即标量乘以矩阵的每一个元素

2.3 单位矩阵和逆矩阵

• 单位矩阵：主对角线为1，其他为0的矩阵
• 逆矩阵：矩阵乘以逆矩阵等于单位矩阵

2.4 线性相关和生成子空间

2.5 范数

2.6 特殊类型的矩阵和向量

2.7 特征分解

2.8 奇异值分解

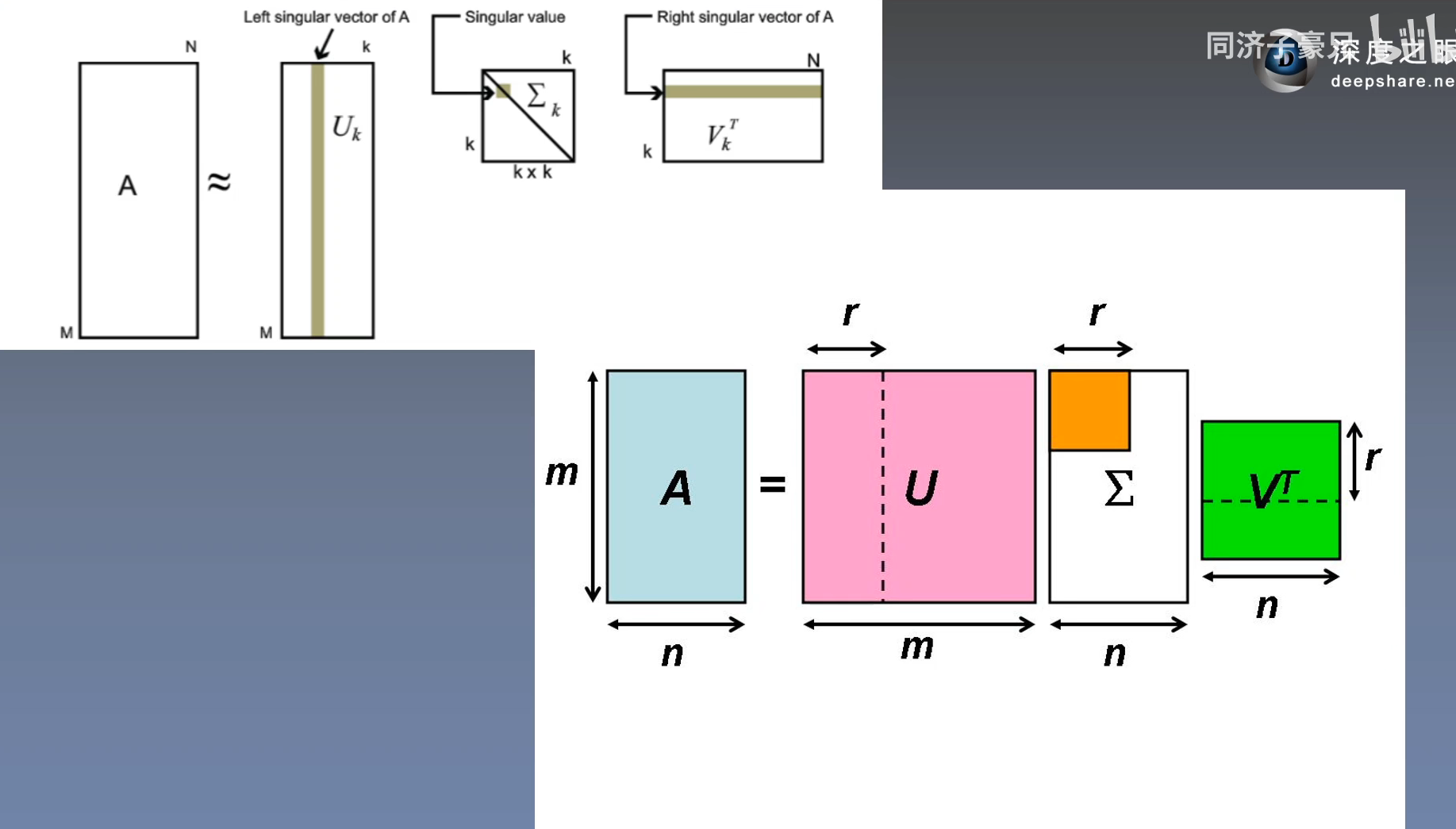
2.9 Moore-Penrose伪逆

2.10 迹运算

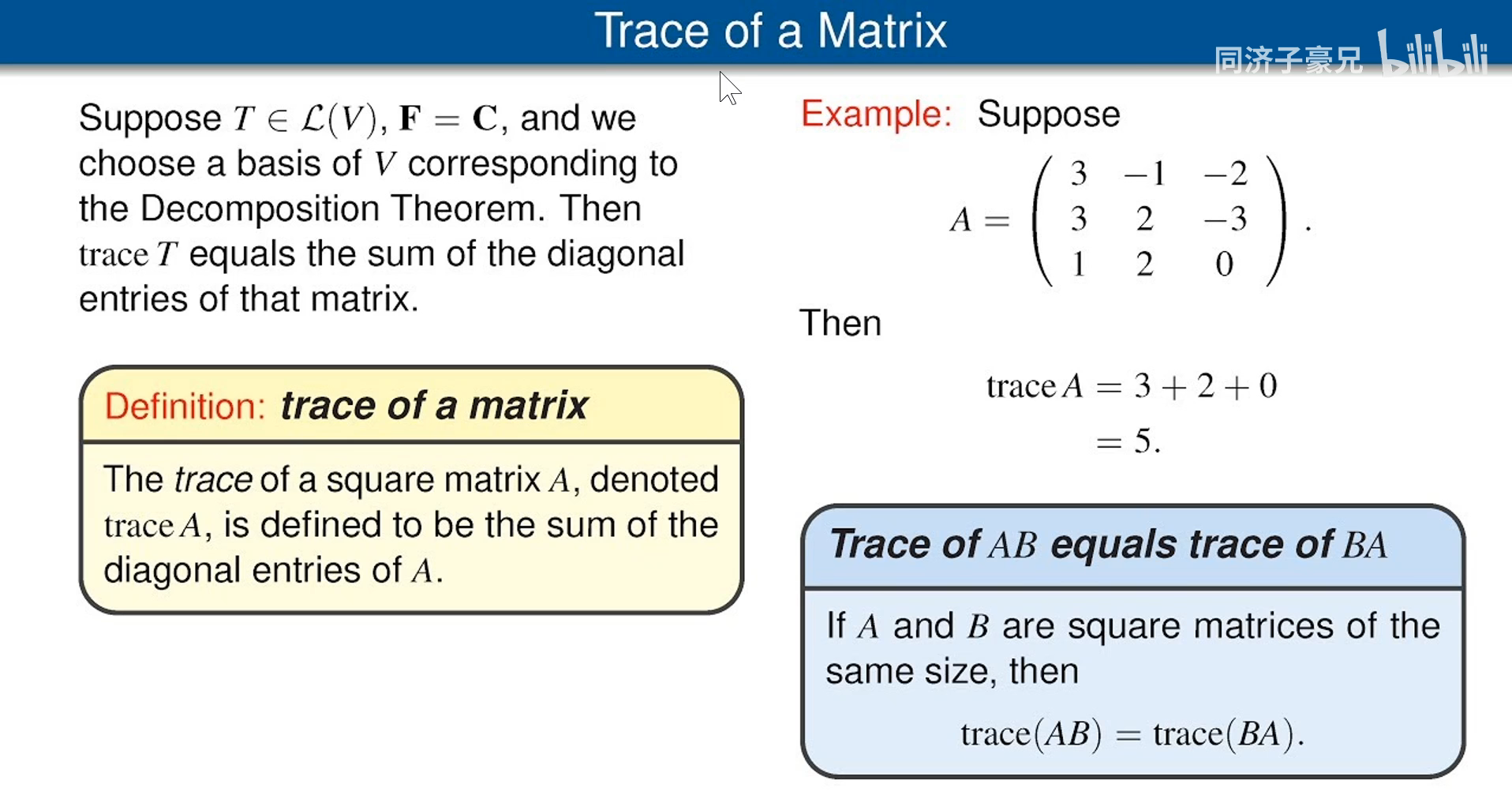
2.11 行列式

2.12 实例：主成分分析

• PCA降维算法

第三章 概率与信息论

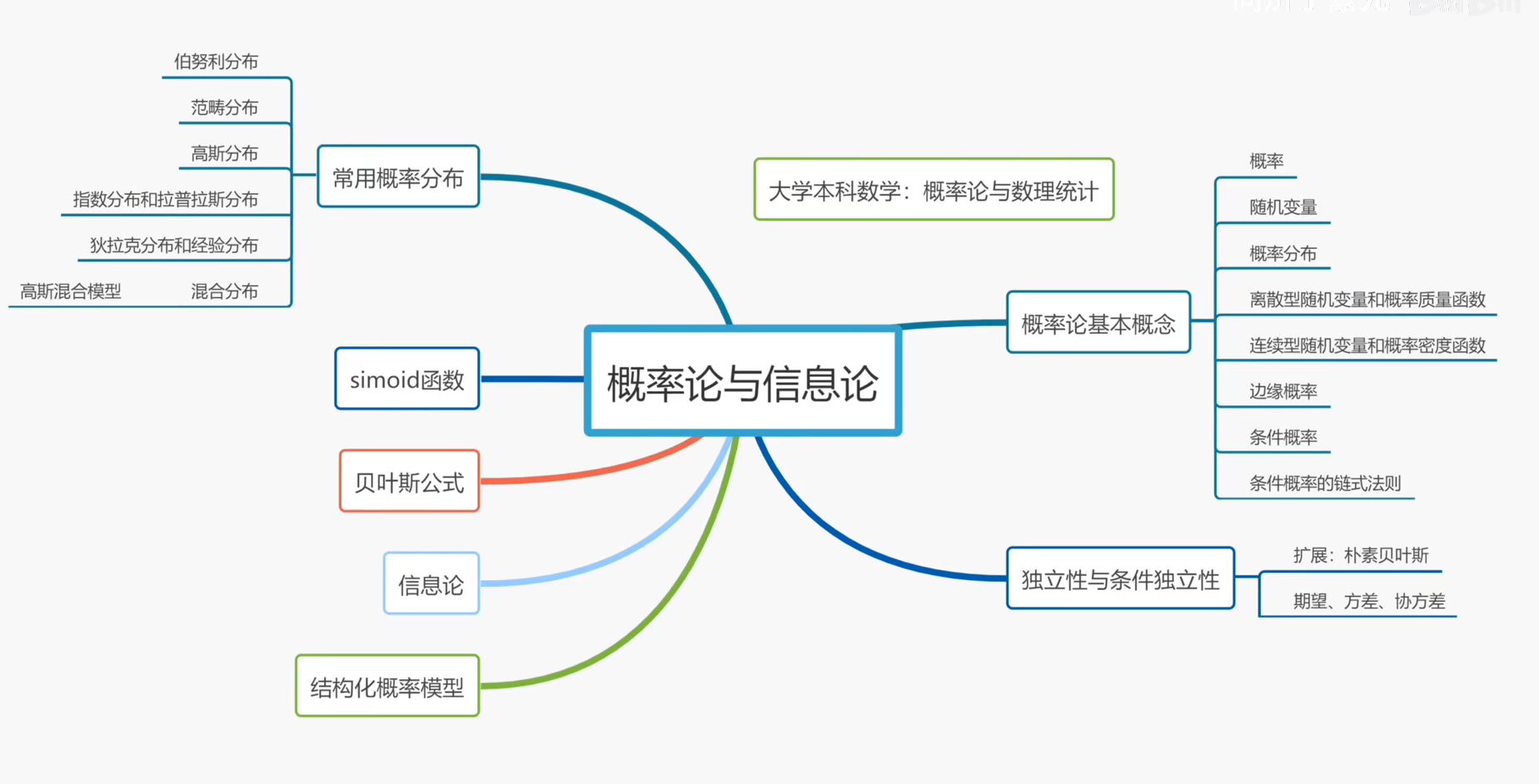
3.1 为什么用使用概率

3.2 随机变量

3.3 概率分布

3.3.1 离散型变量和概率质量函数

3.3.2 连续型变量和概率密度函数

3.4 边缘概率

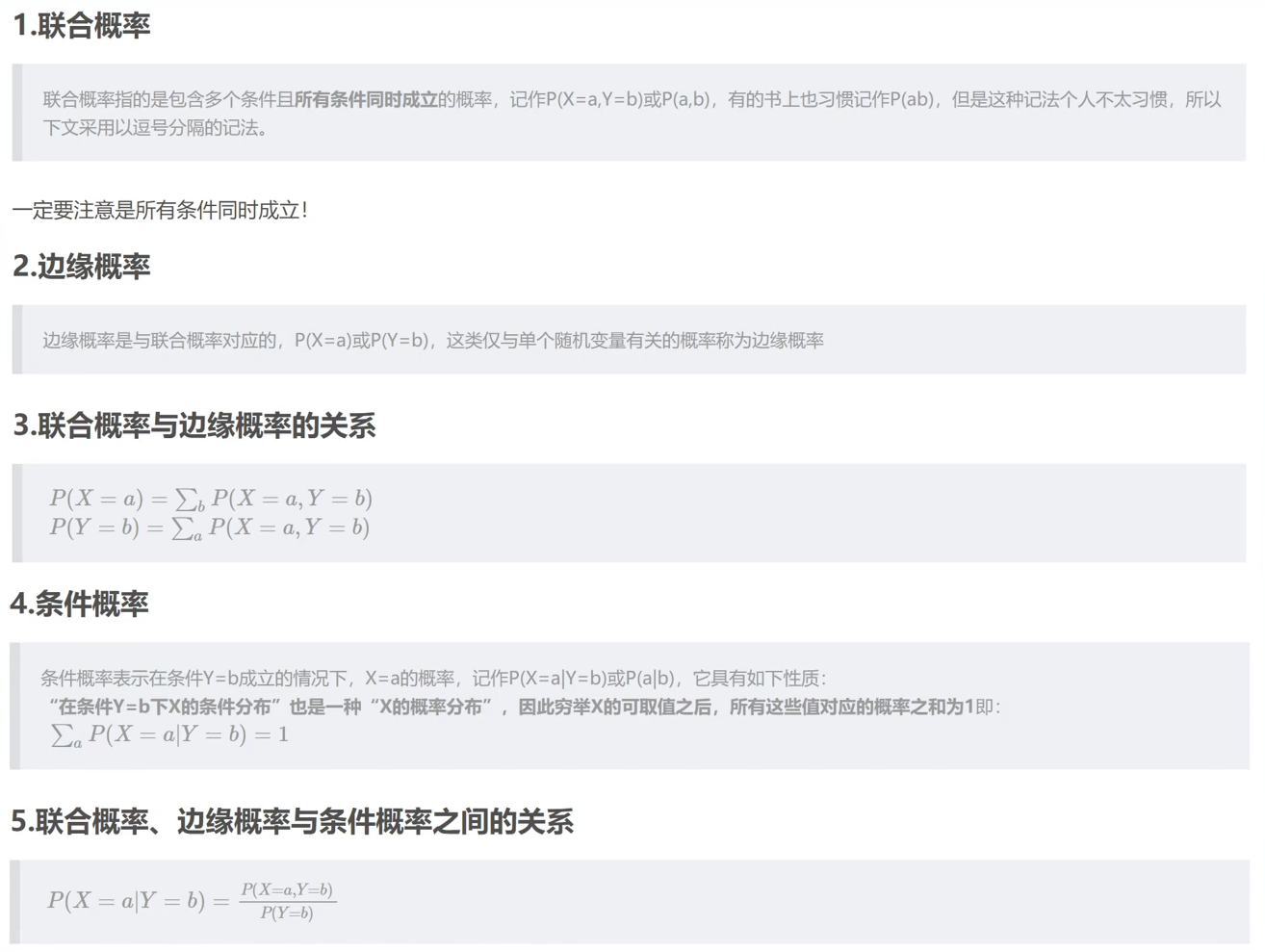
3.5 条件概率

3.6 条件概率的链式法则

3.7 独立性和条件独立性

3.8 期望、方差和协方差

3.9 常用概率分布

3.9.1 Bernoulli分布

3.9.2 Multinoulli分布

3.9.3 高斯分布

3.9.4 指数分布和Laplace分布

3.9.5 Dirac分布和经验分布

3.9.6分布的混合

3.10 常用函数的有用性质

3.11 贝叶斯规则

3.12 连续型变量的技术细节

3.13 信息论

3.14 结构化概率模型

第四章 数值计算

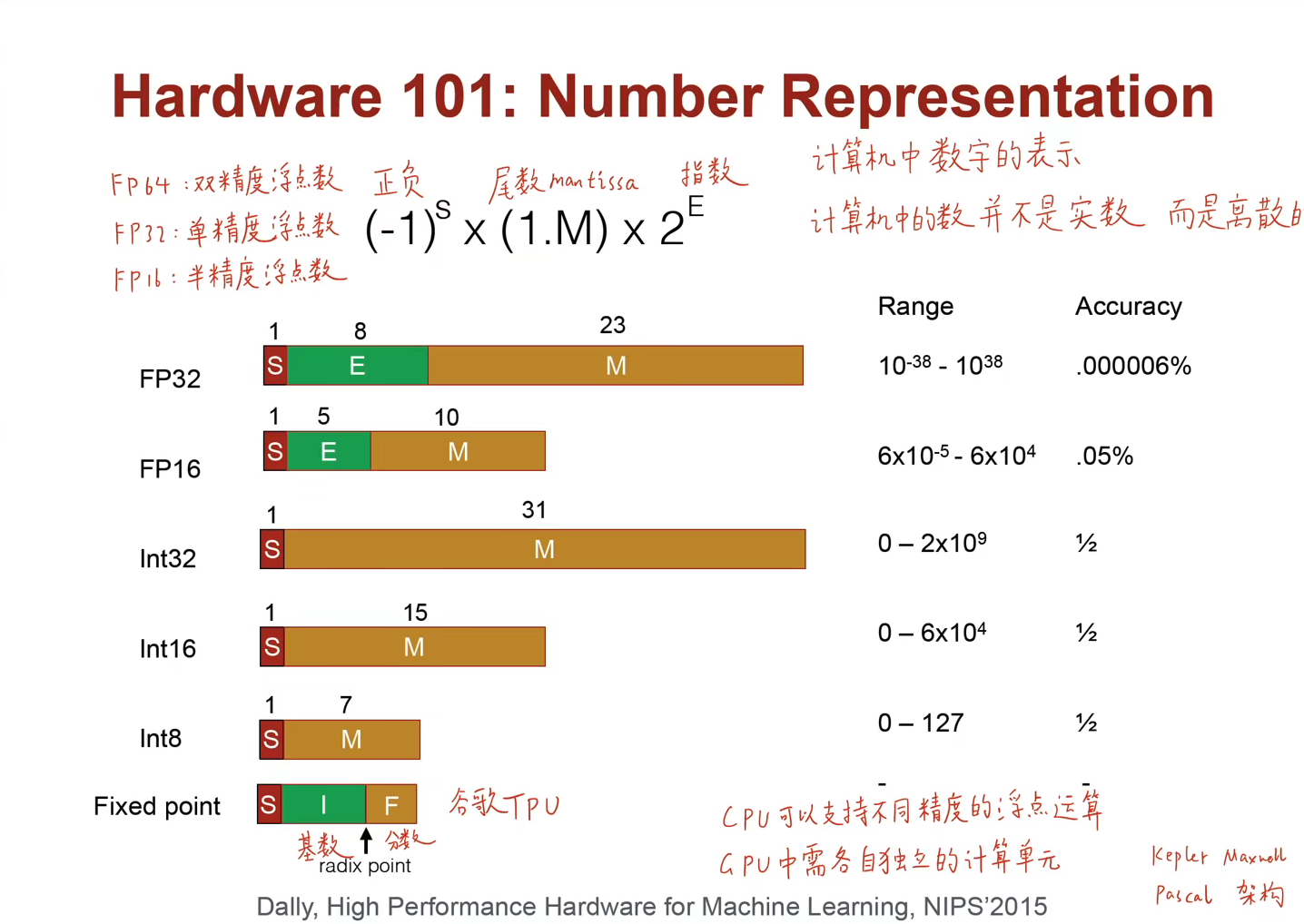
4.1 上溢和下溢

4.2 病态条件

4.3 基于梯度的优化方法

4.3.1 梯度之上：Jacobian和Hessian矩阵

4.4 约束优化

4.5 实例：线性最小二乘

第五章 机器学习基础

• 数值分析库SciPy

5.1 学习算法

5.1.1 任务T

5.1.2 性能度量P

5.1.3 经验E

5.1.4 示例：线性回归

5.2 容量、过拟合和欠拟合

5.2.1 没有免费午餐定理

5.2.2 正则化

5.3 超参数和验证集

5.3.1 交叉验证

5.4 估计、偏差和方差

5.4.1 点估计

5.4.2 偏差

5.4.3 方差和标准差

5.4.4 权衡偏差和方差以最小化均方误差

5.4.5 一致性

5.5 最大似然估计

5.5.1 条件对数似然和均方误差

5.5.2 最大似然的性质

5.6 贝叶斯估计

5.6.1 最大后验(MAP)估计

5.7 监督学习算法

5.7.1 概率监督学习

5.7.2 支持向量机

5.7.3 其他简单的监督学习算法

5.8 无监督学习算法

5.8.1 主成分分析

5.8.2 k-均值聚类

5.9 随机梯度下降

5.10 构建机器学习算法

5.11 促使深度学习发展的挑战

5.11.1 维数灾难

5.11.2 局部不变性和平滑正则化

5.11.3 流形学习

第二部分 深度网络：现代实践

第六章 深度前馈网络

6.1 实践：学习XOR

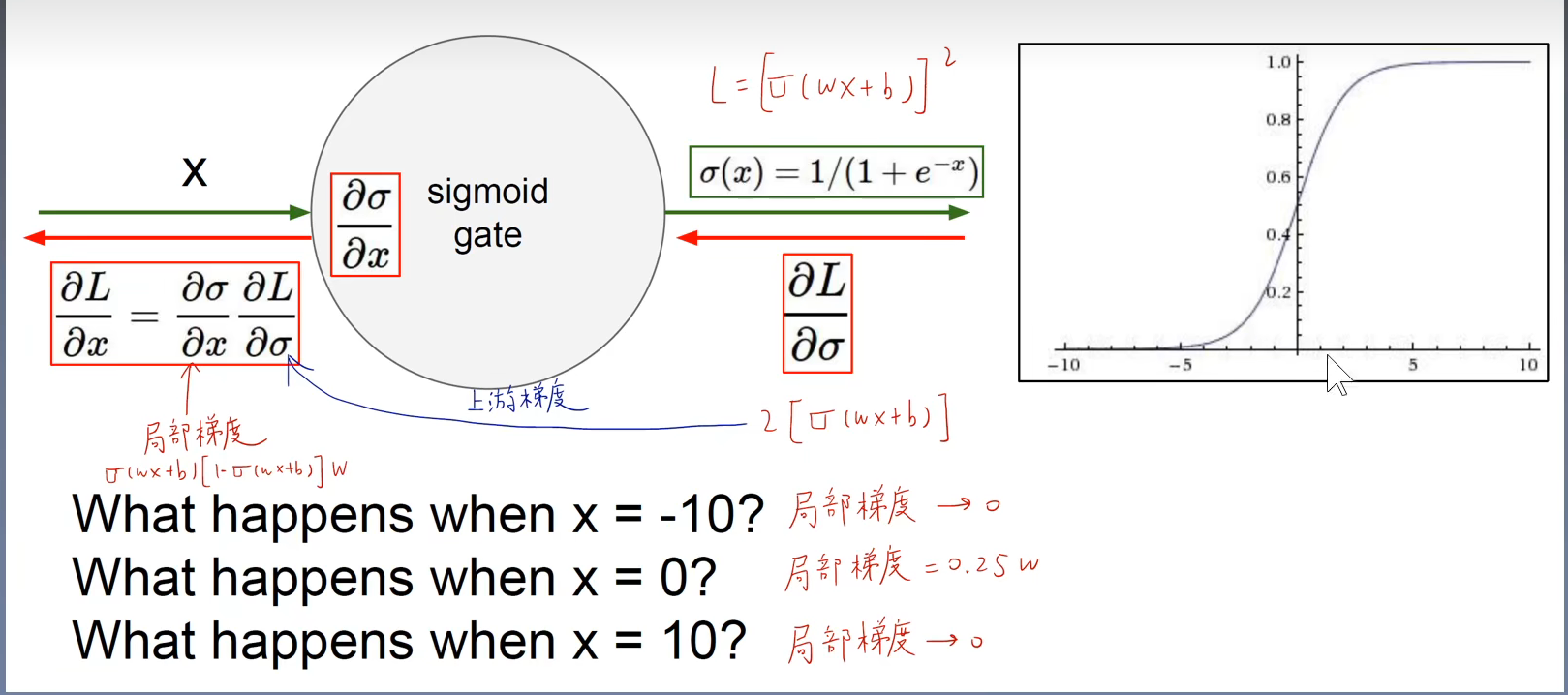
6.2 基于梯度的学习

6.2.1 代价函数

6.2.2 输出单元

6.3 隐藏单元

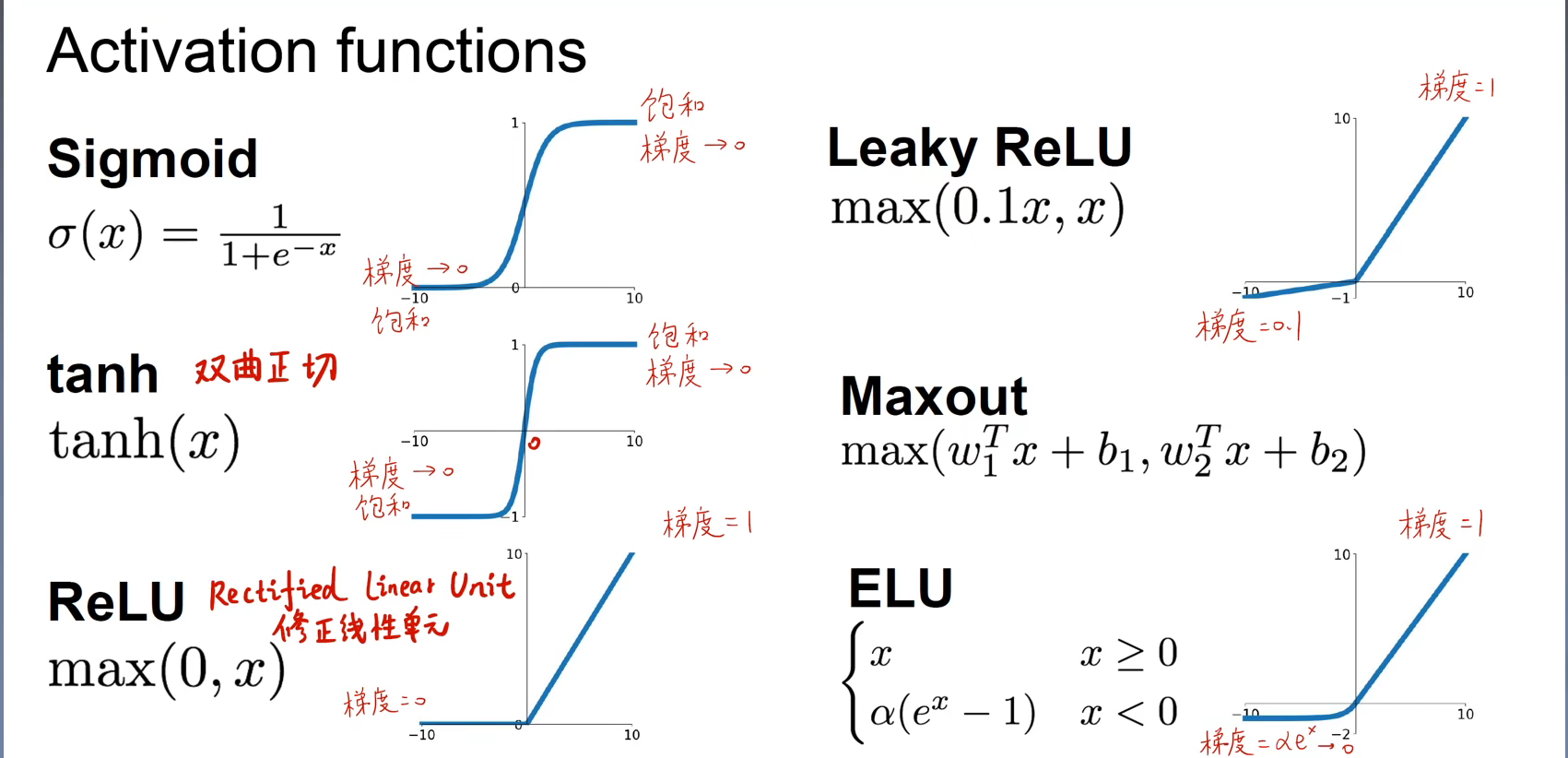
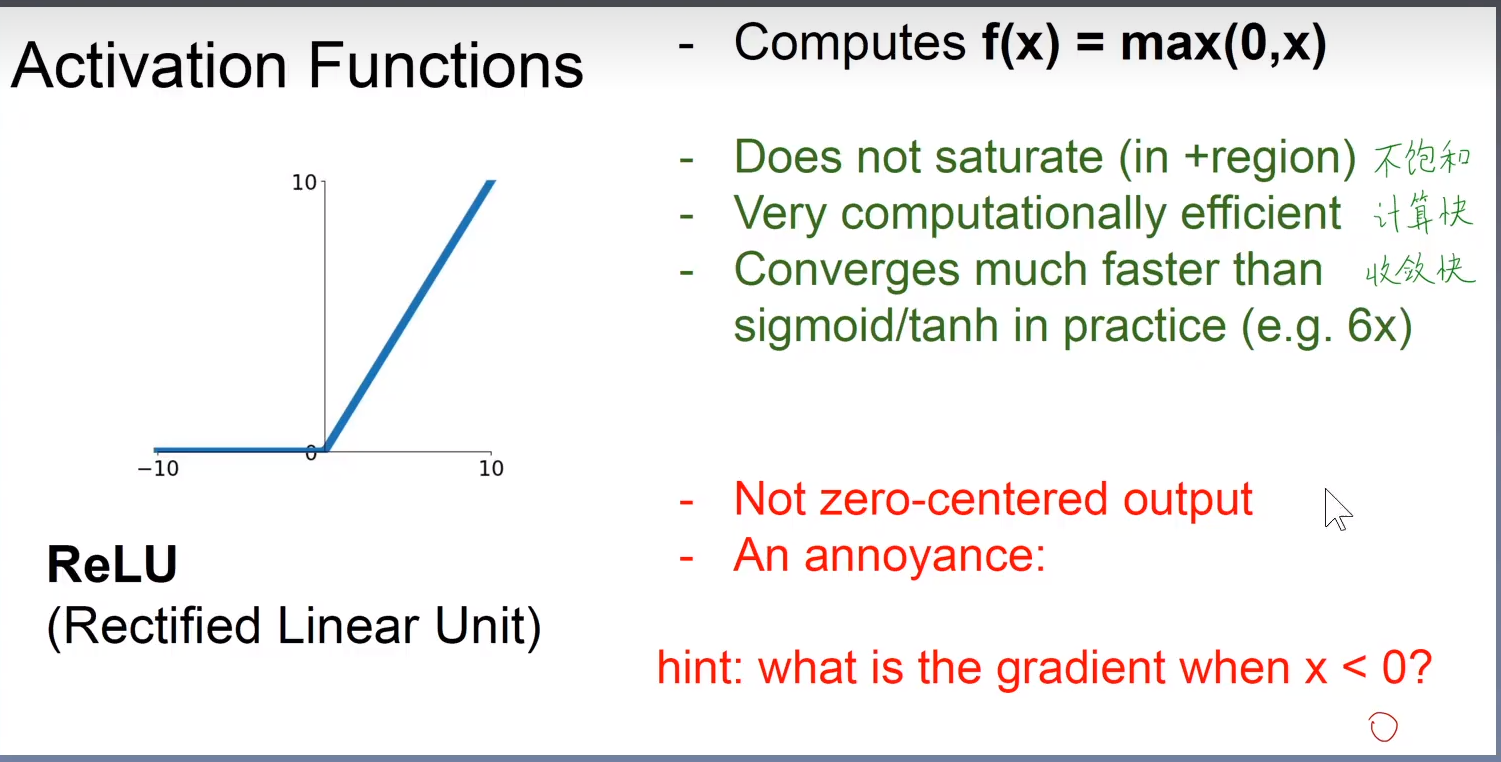
6.3.1 整流线性单元及其扩展

6.3.2 logistic sigmoid与双曲正切函数

6.3.3 其他隐藏单元

6.4 架构单元

6.4.1 万能近似性质和深度

6.4.2 其他架构上的考虑

6.5 反向传播和其他的微分算法

6.5.1 计算图

6.5.2 微积分中的链式法则

6.5.3 递归地使用链式法则来实现反向传播

6.5.4 全连接MLP中的反向传播计算

6.5.5 符号到符号的导数

6.5.6 一般化的反向传播

6.5.7 实例：用于MLP训练的反向传播

6.5.8 复杂化

6.5.9 深度学习界以外的微分

6.5.10 高阶微分

6.6 历史小记

第七章 深度学习中的正则化

7.1 参数范数惩罚

7.1.1 $$L^2$$参数正则化

7.1.2 $$L^1$$正则化

7.2 作为约束的范数惩罚

7.3 正则化和欠约束问题

7.4 数据集增强

7.5 噪声鲁棒性

7.5.1 向输出目标注入噪声

7.6 半监督学习

7.7 多任务学习

7.8 提前终止

7.9 参数绑定和参数共享

7.9.1 卷积神经网络

7.10 稀疏表示

7.11 Bagging和其他集成方法

7.12 Dropout

7.13 对抗训练

7.14 切面距离、正切传播和流形正切分类器

第八章 深度模型中的优化

8.1 学习和纯优化有什么不同

8.1.1 经验风险最小化

8.1.2 代理损失函数和提前终止

8.1.3 批量算法和小批量算法

8.2 神经网络优化中的挑战

8.2.1 病态

8.2.2 局部极小值

8.2.3 高原、鞍点和其他平坦区域

8.2.4 悬崖和梯度爆炸

8.2.5 长期依赖

8.2.6 非精确梯度

8.2.7 局部和全局结构间的弱对应

8.2.8 优化的理论限制

8.3 基本算法

8.3.1 随机梯度下降

8.3.2 动量

8.3.3 Nesterov动量

8.4 参数初始化策略

8.5 自适应学习率算法

8.5.1 AdaGrad

8.5.2 RMSProp

8.5.3 Adam

8.5.4 选择正确的优化算法

8.6 二阶近似方法

8.6.1 牛顿法

8.6.2 共轭梯度

8.7 优化策略和元算法

8.7.1 批标准化

8.7.2 坐标下降

8.7.3 Polyak平均

8.7.4 监督预训练

8.7.5 设计有助于优化的模型

8.7.6 延拓法和课程学习

第九章 卷积网络

9.1 卷积运算

9.2 动机

9.3 池化

9.4 卷积与池化作为一种无限强的先验

9.5 基本卷积函数的变体

9.6 结构化输出

9.7 数据类型

9.8 高效的卷积算法

9.9 随机或无监督的特征

9.10 卷积网络的神经科学基础

9.11 卷积网络与深度学习的历史

第十章 序列建模：循环和递归网络

10.1 展开计算图

10.2 循环神经网络

10.2.1 导师驱动过程和输出循环网络

10.2.2 计算循环神经网络的梯度

10.2.3 作为有向图模型的循环网络

10.2.4 基于上下文的RNN序列建模

10.3 双向RNN

10.4 基于编码-解码的序列到序列架构

10.5 深度循环网络

10.6 递归神经网络

10.7 长期依赖的挑战

10.8 回声状态网络

10.9 渗漏单元和其他多时间尺度的策略

10.9.1 时间维度的跳跃连接

10.9.2 渗漏单元和一系列不同时间尺度

10.10 长短期记忆和其他门控RNN

10.10.1 LSTM

10.10.2 其他门控RNN

10.11 优化长期依赖

10.11.1 截断梯度

10.11.2 引导信息流的正则化

10.12 外显记忆

第十一章 实践方法论

11.1 性能度量

11.2 默认的基准模型

11.3 决定是否收集更多数据

11.4 选择超参数

11.4.1 手动调整超参数

11.4.2 自动超参数优化算法

11.4.3 网络搜索

11.4.4 随机搜索

11.4.5 基于模型的超参数优化

11.5 调试策略

11.6 示例：多位数字识别

第十二章 应用

12.1 大规模深度学习

12.1.1 快速的CPU实现

12.1.2 GPU实现

12.1.3 大规模的分布式实现

12.1.4 模型压缩

12.1.5 动态结构

12.1.6 深度网络的专用硬件实现

12.2 计算机视觉

12.2.1 预处理

12.2.2 数据集增强

12.3 语音识别

12.4 自然语言处理

12.4.1 n-gram

12.4.2 神经语言模型

12.4.3 高维输出

12.4.4 结合n-gram和神经语言模型

12.4.5 神经机器翻译

12.4.6 历史展望

12.5 其他应用

12.5.1 推荐系统

12.5.2 知识表示、推理和回答

第三部分 深度学习研究

第十三章 线性因子模型

13.1 概率PCA和因子分析

13.2 独立成分分析

13.3 慢特征分析

13.4 稀疏编码

13.5 PCA的流形解释

第十四章 自编码器

14.1 欠完备自编码器

14.2 正则自编码器

14.2.1 稀疏自编码器

14.2.2 去噪自编码器

14.2.3 惩罚导数作为正则

14.3 表示能力、层的大小和深度

14.4 随机编码器和解码器

14.5 去噪自编码器详解

14.5.1 得分估计

14.5.2 历史展望

14.6 使用自编码器学习流形

14.7 收缩自编码器

14.8 预测稀疏分解

14.9 自编码器的应用

第十五章 表示学习

15.1 贪心逐层无监督预训练

15.1.1 何时以及为何无监督预训练有效

15.2 迁移学习和领域自适应

15.3 半监督解释因果关系

15.4 分布式表示

15.5 得益于深度的指数增益

15.6 提供发现潜在原因的线索

第十六章 深度学习中的结构化概率模型

16.1 非结构化建模的挑战

16.2 使用图描述模型结构

16.2.1 有向模型

16.2.2 无向模型

16.2.3 配分模型

16.2.4 基于能量的模型

16.2.5 分离和d-分离

16.2.6 在有向模型和无向模型中转换

16.2.7 因子图

16.3 从图模型中采样

16.4 结构化建模的优势

16.5 学习依赖关系

16.6 推断和近似推断

16.7 结构化概率模型的深度学习方法

16.7.1 实例：受限玻尔兹曼机

第十七章 蒙特卡罗方法

17.1 采样和蒙特卡罗方法

17.1.1 为什么需要采样

17.1.2 蒙特卡罗采样的基础

17.2 重要采样

17.3 马尔可夫链蒙特卡罗方法

17.4 Gibbs采样

17.5 不同的峰值之间的混合挑战

17.5.1 不同峰值之间通过回火来混合

17.5.2 深度也许会有助于混合

第十八章 直面配分函数

18.1 对数似然梯度

18.2 随机最大似然和对比散度

18.3 伪似然

18.4 得分匹配和比率匹配

18.5 去噪得分匹配

18.6 噪声对比估计

18.7 估计配分函数

18.7.1 退火重要采样

18.7.2 桥式采样

第十九章 近似推断

19.1 把推断视作优化问题

19.2 期望最大化

19.3 最大后验推断和稀疏编码

19.4 变分推断和变分学习

19.4.1 离散型潜变量

19.4.2 变分法

19.4.3 连续型潜变量

19.4.4 学习和推断之间的相互作用

19.5 学成近似推断

19.5.1 醒眠算法

19.5.2 学成推断的其他形式

第二十章 深度生成模型

20.1 玻尔兹曼机

20.2 受限玻尔兹曼机

20.2.1 条件分布

20.2.2 训练受限玻尔兹曼机

20.3 深度信念网络

20.4 深度玻尔兹曼机

20.4.1 有趣的性质

20.4.2 DBM均匀场推断

20.4.3 DBM的参数学习

20.4.4 逐层预训练

20.4.5 联合训练深度玻尔兹曼机

20.5 实值数据上的玻尔兹曼机

20.5.1 Gaussian-Bernoulli RBM

20.5.2 条件协方差的无向模型

20.6 卷积玻尔兹曼机

20.7 用于结构化或序列输出的玻尔兹曼机

20.8 其他玻尔兹曼机

20.9 通过随机操作的反向传播

20.9.1 通过离散随机操作的反向传播

20.10 有向生成网络

20.10.1 sigmoid信念网络

20.10.2 可微生成器网络

20.10.3 变分自编码器

20.10.4 生成式对抗网络

20.10.5 生成矩匹配网络

20.10.6 卷积生成网络

20.10.7 自回归网络

20.10.8 线性自回归网络

20.10.9 神经自回归网络

20.10.10 NADE

20.11 从自编码器采样

20.11.1 与任意去噪自编码器相关的马尔可夫链

20.11.2 夹合与条件采样

20.11.3 回退训练过程

20.12 生成随机网络

20.12.1 判别性GSN

20.13 其他生成方案

20.14 评估生成模型

20.15 结论